All participants in this study were southern Han Chinese from the Guangdong province of China. Whole blood samples and the electronic medical records of each participant were collected between 2008 to 2012 and studied retrospectively. Inclusion criteria for the PCAD group were: (1) males aged 55 years and females aged 65 years [18]; (2) coronary angiography showing that at least one vessel in the left coronary artery trunk, left anterior descending branch (including main diagonal branch), circumflex branch (including main marginal branch) or right coronary artery (including posterior descending branch or left ventricular posterior collateral branch) had $\ge$50% degree of stenosis. The inclusion criteria for the control group were: males aged $\ge$55 years and females aged $\ge$65 years; no CAD diagnosed by coronary angiography, no symptoms such as chest tightness or chest pain, and no myocardial ischemia revealed by echocardiography. Exclusion criteria: participants with malignant tumors, multiple organ failure, or severe immune diseases were excluded from the study.

A total of 140 patients with PCAD and 195 controls were selected as the subjects in this study. After the exclusion of individuals whose SNP genotype information or clinical data could not be obtained, 131 patients with PCAD and 187 controls were included in the final analysis.

Two milliliters of whole blood was collected from each individual in an ethylenediamine tetra-acetic acid disodium (EDTA) anticoagulant tube. The following information was collected from the electronic medical record of each participant: sex, age, smoking history, hypertension, diabetes, hyperlipidemia, as well as biochemical test results for high-density lipoprotein cholesterol (HDL-c), LDL-c, glucose (GLU), TG and total cholesterol (CHOL).

Peripheral blood samples were used to isolate the genomic DNA with the E-Z 96${}^{\text{TM}}$ Blood DNA Kit (OMEGA, USA) according to the manufacturer’s instructions. The integrity of genomic DNA was confirmed by 1% agarose gel electrophoresis and the concentration determined using a Spectrophotometer ND 1000. Each DNA sample was diluted to a concentration of 5 ng/$\mu$L and stored at –20 °C until use.

Candidate SNPs were selected from SNPs previously reported in the literature to be associated with CAD or with carotid intima-media thickness. Those with a frequency of 0.05 were excluded, meaning that 48 bi-allelic SNPs were included in this study. Detailed information on these candidate SNPs is shown in Supplementary Table 1.

SNPs were genotyped using multiplex polymerase chain reaction (PCR) and single base primer extension in a 48-PLEX GENOMELAB SNPSTREAM® system. Briefly: 96 unique primers (shown in Supplementary Table 2) having no interaction with each other were designed using the Beckman Coulter’s Autoprimer multiplex primer design system for 48-plex PCR. The primers were automatically divided into 6 categories according to the allele type: C/A, T/A, A/G, C/G, T/C and T/G. The 5-prime end of each was linked with a tag sequence that was complementary to the corresponding tag sequence in the SNPware tag array board. The primers and enzyme mix for SNPstream analysis were provided by Beckman Coulter’s Biomek® FX. SNPstream analysis was performed on the Beckman Coulter’s Biomek® FX automatic laboratory workstation, resulting in genotype information for each SNP.

Associations between SNP genotype or allelotype and PCAD were analyzed with the PLINK-model program package. This performs four tests (1df dominant gene action, 1df recessive gene action, 2df genotypic, and Cochran-Armitage trend) and outputs the combined results. Correlations were evaluated with the Chi-square test and an asymptotic p-value was produced. A significant correlation was considered as p 0.05. Interactions between SNPs were analyzed using the GMDR model, and multi-site genotypes were divided into high risk and low risk groups. Cross-validation and overlapping tests (permutation) were used to estimate correlations between these gene combinations and diseases. The best model was judged as having an accuracy of $>$50% and a consistent rate of cross-validation of $\ge$5/10 [19, 20].

General statistical analysis was performed using the statistical package R (https://www.r-project.org/; version x64 4.0.2). Classification variables were represented by n (%), and the significance of differences between groups was tested using Pearson’s Chi-squared test with Yates’ continuity correction. Continuous variables with a normal distribution and homogeneous variance were represented as the mean $\pm$ SD, with the Student’s t test used to evaluate the significance of differences between groups. Continuous variables that did not conform to the normal distribution or homogeneous variance were represented as the median (interquartile range), and the Wilcoxon rank sum test with continuity correction was used to test the significance of differences between these groups. Statistical significance was considered as p 0.05.

SNPs and TCRFs with a missing value ratio of greater than 20% were excluded. Feature combination (FC) was used to indicate all independent variables (termed “feature” in ML) that were combined to build a ML model. FCs were determined in 3 ways. (1) The FCs included SNPs or TCRFs that showed a significant difference (sd-SNPs and sd-TCRFs, respectively) between the PCAD and control groups, as well as the sd-SNP plus the sd-TCRFs. (2) The features in the FCs were selected from the sd-SNPs and the sd-TCRFs, or from the SNPs with a differential trend (dt-SNPs) (p 0.2) in genetic model analysis and the sd-TCRFs, using the least absolute shrinkage and selection operator (LASSO) regression method. (3) The FC consisted of one to eight factors that were randomly selected from the sd-SNPs and the sd-TCRFs, or from the dt-SNPs and the sd-TCRFs, by using the iterator ‘combinations’ in the Python module ‘itertools’.

Next, for each FC a new data sheet was generated from the original data wherein the variables in the new data were the factors included in the FC and the response variable (group). In each new data sheet, the rows with missing values were removed. The remained rows were then divided into a training dataset and a test dataset using Scikit-learn (https://scikit-learn.org/stable/; v.0.23.1) (function ‘train_test_split’ with test_size = 0.25, random_state = 0). The training dataset was used to construct the classifier, while the test dataset was used to evaluate performance. ‘StandardScaler’ function in the Scikit-learn module was used to standardize the feature values of continuous variables before constructing the logistic regression classifier.

Scikit-learn is a Python module that integrates a wide range of state-of-the-art ML algorithms for medium-scale supervised and unsupervised problems [21]. RFC, LRC and GBC are used to build classifiers for predicting disease risk, progression, prognosis, and so on. RFC in the ‘sklearn.ensemble’ module is one of the averaging algorithms in ensemble methods and is a perturb-and-combine technique specifically designed for trees. In practice, variance reduction due to the introduction of randomness in the classifier construction is often significant, hence yielding a better model overall [22]. The probabilities that describe possible outcomes of a single trial are modeled using a logistic function known as LRC in the ‘sklearn.linear_model’. GBC is a boosting method and builds an additive model in a forward stage-wise fashion that allows for the optimization of arbitrary differentiable loss functions. Base estimators in GBC are built sequentially, with several weak models having to be combined to produce a powerful ensemble that reduces the bias of the combined estimator [23]. The classifiers constructed with the ML algorithm of RFC, LRC or GBC are referred to in this study as the RFC model (RFCM), LRC model (LRCM) and GBC model (GBCM), respectively.

The classifiers for each FC in this study were built using RFC, LRC and GBC in the Scikit-learn module and with the training dataset. Five-fold cross for model validation was performed and the hyper-parameters for model tuning are shown in Supplementary Table 3. The predictive performance of the classifiers was evaluated with the test dataset by computing the area under the receiver operating characteristic curve (AUC), sensitivity, specificity and average precision (AP) for the prediction of positive cases (using the ‘sklearn.metrics.auc’, ‘sklearn.metrics.recall_score’ and ‘sklearn.metrics.plot_precision_recall_curve’ functions, respectively). The final models and FCs were determined according to the performance of the models, with higher AUC and sensitivity corresponding to better performance.

Nomograms representing a regression model (lrm) fitted with ‘rms’ were drawn with the nomogram model in the ‘rms’ R package, which can be used manually to obtain predicted values. The nomogram has a reference line for reading scoring points (default range 0–100). Once the reader manually totals the points, the predicted values can be read at the bottom. Bias-corrected (overfitting-corrected) estimates of predicted vs. observed values were performed with the ‘calibrate’ model in the ‘rms’ R package by using bootstrapping (B = 1000) or cross-validation. Validation of ‘lrm’ models was performed with the ‘validate’ function in the ‘rms’ R package using the training dataset followed by the test dataset. The performance of the nomogram model for predicting outcomes was evaluated by calculating the concordance index (C-index). The nomogramFomula R package was used to calculate the total nomogram points for each sample, and optimal cutpoints for each nomogram model were computed with the OptimalCutpoints R package (methods = “Youden”). Decision curve analysis for each ‘lrm’ model was performed with the ‘rmda’ R package.

Fig. 1 shows the design of the study and the process of data acquisition, data processing, model construction and verification.

Fig. 1.

The flow chart of this study. PCAD, premature coronary artery disease; CVD, cardiovascular disease; AUC, the area under the receiver operating characteristic curve; C-index, consistency index; SNP, single nucleotide polymorphism; TCRF, traditional cardiovascular risk factor; LRCM, logistic regression classifier model; RFCM, random forest classifier model; GBCM, gradient boosting classifier model.

The aim of this study was not to identify PCAD-related SNPs that were independent of TCRFs, but rather to construct ML models with predictors that included TCRF and SNP information and to assess whether these had superior performance compared to ML models built with TCRF predictors only. Hence, the present study was different to usual case-control studies in that the TCRFs were intentionally not matched between the two groups.

There was no significant difference in the gender ratio between the PCAD and control groups. The median age of the PCAD and control groups was 48 and 68 years, respectively, with the control group being older due to the admission criteria. The incidence of smoking, hypertension, diabetes, and hyperlipidemia were all significantly higher in the PCAD group than in the control group. Plasma levels of GLU and TG in the PCAD group were significantly higher than in the control group, whereas HDL-c was significantly lower. There was no significant difference in the plasma levels of CHOL and LDL-c between the two groups (Table 1).

Of the 48 SNP loci examined, three SNPs (rs3791398, rs1256049 and rs2071406) failed genotyping and were excluded from further analysis. rs10757274, rs10757278 and rs2383206 each showed a significant correlation with PCAD using the recessive and genotype genetic model test (p 0.05). rs7291467 was significantly correlated with PCAD using the ‘trend’, ‘allelic’ and ‘dominant’ genetic model test (p 0.05). Comparison between groups of the variables that were selected to construct models was shown in Supplementary Table 4.

MDR analysis revealed the best single factor model that correlated with PCAD was rs10757274. The cross-validation consistency of this model was 7/10, and the test balance accuracy was 0.533. The best two-factor model that correlated with PCAD was comprised of rs10757274 and rs3850641, with a cross-validation consistency of 5/10, a test balance accuracy of 0.564 and a sign test p-value of 0.055. The best three-factor model was comprised of rs2048327, rs16147 and rs1801708, and showed the highest training balance accuracy (0.680), the lowest detection balance accuracy (0.477), and the lowest consistency of cross-validation (3/10) (Table 2). Therefore, the two-factor model obtained by MDR analysis was considered to be the best model. Fig. 2 shows the interaction between the two-locus genotypes. The combinations of rs10757274 (GA) with rs3850641 (AA), and of rs10757274 (GG) with rs3850641 (GA) were associated with an increased risk of PCAD.

Fig. 2.

PCAD risk associated interaction between the SNPs. In each cell, the left bar indicates the positive score, the right bar represents the negative score. When the absolute value of the positive score is greater than that of the negative score, increased risk is considered in the cell, otherwise, decreased risk in the cell. Risk-increased cells are indicated by dark gray, risk-decreased cells by light gray, and empty cells by white. (A) The best single factor model for correlation between SNPs and PCAD. (B) The best two-factor model for correlation between SNPs and PCAD.

The AUCs of the LRCM, RFCM and GBCM constructed with four sd-SNPs (rs10757274, rs10757278, rs2383206 and rs7291467) were 0.61, 0.63 and 0.62, respectively (Fig. 3A). The AUCs of the LRCM, RFCM and GBCM built with 7 sd-TCRFs (smoking, hypertension, hyperlipemia, diabetes, Glu, TG and HDL-c) were 0.82, 0.85 and 0.84, respectively (Fig. 3B). The AUCs of the LRCM, RFCM and GBCM constructed with four sd-SNPs plus 7 sd-TCRFs were 0.88, 0.85 and 0.86, respectively (Fig. 3C). The performance of the classifiers constructed with the sd-SNPs plus the sd-TCRFs was slightly improved.

Fig. 3.

The receiver operating characteristic curve (ROC) of the classifiers constructed using the factors significantly associated with PCAD. LogisticRegression, RandomForestClassifier, and GradientBoostingClassifier are three different machine learning algorithms. GLU, Glucose; TG, triglycerides; HDL, high density lipoprotein cholesterol. (A) The ROC of the classifiers constructed with the sd-SNPs. (B) The ROC of the classifiers constructed with the sd-TCRFs. (C) The ROC of the classifiers constructed with the sd-SNPs plus the sd-TCRFs.

An optimized FC with 7 features (LASSO-7F-FC: rs10757274, rs10757278, smoking, diabetes, hyperlipemia, GLU and HDL-c) was selected by using the LASSO regression model from the sd-SNPs and sd-TCRFs (Fig. 4A). The AUCs of the LRCM, RFCM and GBCM constructed with the LASSO-7F-FC were 0.89, 0.84 and 0.84, respectively (Fig. 4B). The APs of the classifiers for the prediction of PCAD were 0.86, 0.78 and 0.78, respectively (Fig. 4C), while the sensitivity of the classifiers was 0.71. An optimized FC with 8 features (LASSO-8F-FC: rs10757278, rs4537545, smoking, hypertension, diabetes, hyperlipemia, GLU and HDL-c) was selected using the LASSO regression method from 18 dt-SNPs (including sd-SNPs) and sd-TCRFs (Fig. 4D). The AUCs of the LRCM, RFCM and GBCM constructed with the LASSO-8F-FC were 0.84, 0.86 and 0.83, respectively (Fig. 4E). The APs of the classifiers for the prediction of PCAD were 0.78, 0.77 and 0.76, respectively (Fig. 4F), while the sensitivity of the classifiers was 0.64. Although the classifiers built with LASSO-7F-FC and with LASSO-8F-FC showed high accuracy, their low sensitivity makes them less useful for identifying individuals at high risk for PCAD.

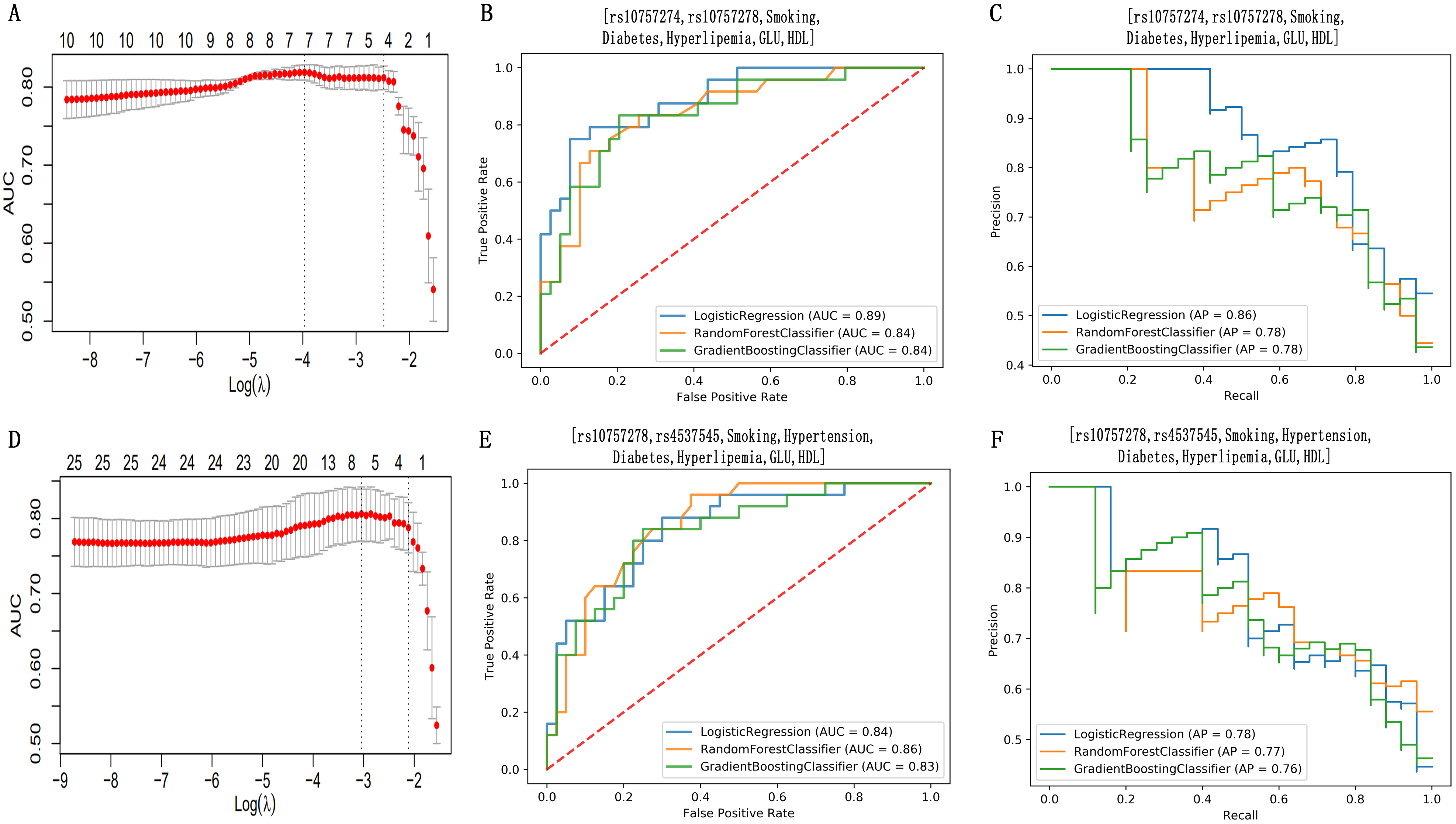Fig. 4.

Feature selection using the least absolute shrinkage and selection operator (LASSO) regression method and the performance assessment for the classifiers established with the features selected with LASSO. The $\lambda$ is a parameter capable of tuning to control the overall strength of the penalty in the LASSO regression process. Identification of the optimal LASSO model was performed via 3-fold cross-validation based on the value of lambda that gives minimum mean cross-validated error. The AUC was plotted verse log($\lambda$). Red dots represent average AUC for each model with a given $\lambda$, and the dotted vertical lines represent the optimal values of $\lambda$. The features in the optimal LASSO models were assessed by building classifiers using machine learning algorithm. (A) Variation of the AUC of the LASSO models fitted with the sd-SNPs plus the sd-TCRFs as tuning the parameter $\lambda$. (B) The receiver operating characteristic curve (ROC) of the classifiers constructed with the features selected by LASSO in (A). (C) The precision recall curve (PRC) of the classifiers constructed with the features selected by LASSO in (A). (D) Variation of the AUC of the LASSO models fitted with the dt-SNPs plus the sd-TCRFs as tuning the parameter $\lambda$. (E) The ROC of the classifiers constructed with the features selected by LASSO in (D). (F) The PRC of the classifiers constructed with the features selected by LASSO in (D).

LASSO regression analysis showed that increasing the number of features beyond 8 did not improve the performance of the model. Therefore, only FCs containing one to eight factors were randomly selected using an iterator and subsequently used to establish classifiers. Among the FCs composed of features randomly selected from the sd-SNPs and sd-TCRFs (RS-SD-FCs), we found that RS-SD-FC1 (rs2383206, smoking, diabetes, hyperlipemia, TG, HDL-c), RS-SD-FC2 (rs10757278, diabetes, hyperlipemia, GLU, TG, HDL-c) and RS-SD-FC3 (rs10757274, rs7291467, smoking, diabetes, hyperlipemia, GLU, TG) could be used to construct classifiers with high performance (Supplementary Fig. 1A,D,G). Indeed, classifiers built with RS-SD-FC1, RS-SD-FC2 and RS-SD-FC3 showed better performance than those constructed by LASSO-8F-FC and LASSO-7F-FC. RS-SD-FC1, RS-SD-FC2 and RS-SD-FC3 were each comprised of one or two sd-SNPs and several sd-TCRFs. Classifiers built only with sd-SNPs (Supplementary Fig. 1B,E,H) or only with sd-TCRFs (Supplementary Fig. 1C,F,I) showed markedly lower performance (Supplementary Fig. 1).

Among the FCs containing features that were randomly selected from dt-SNPs and sd-TCRFs (RS-DT-FCs), we found that RS-DT-FC1 (rs2259816, rs1378577, rs10757274, rs4961, smoking, hyperlipemia, GLU, TG), RS-DT-FC2 (rs1378577, rs10757274, smoking, diabetes, hyperlipemia, GLU, TG) and RS-DT-FC3 (rs1169313, rs5082, rs9340799, rs10757274, rs1152002, smoking, hyperlipemia, HDL-c) could be used to build classifiers with high performance (Fig. 5A,C,E). All of the AUCs for the classifiers built with RS-DT-FC1, RS-DT-FC2 and RS-DT-FC3 using LRC, RFC or GBC were higher than 0.90 (Fig. 5A,C,E). Classifiers constructed with RS-DT-FC1 or RS-DT-FC2 had an AP of $>$0.90 for the prediction of PCAD (Fig. 5B,D), while the classifier built with RS-DT-FC3 had a lower AP (Fig. 5F).

Fig. 5.

Comparison of the performance of the classifiers built with three FCs composed of the factors that were randomly selected from the dt-SNPs and sd-TCRFs. (A) The ROC of the classifiers constructed with RS-DT-FC1 (rs2259816, rs1378577, rs10757274, rs4961, Smoking, Hyperlipemia, GLU, TG). (B) The precision recall curve (PRC) of the classifiers constructed with the RS-DT-FC1. (C) The ROC of the classifiers constructed with RS-DT-FC2 (rs1378577, rs10757274, Smoking, Diabetes, Hyperlipemia, GLU, TG). (D) The PRC of the classifiers constructed with RS-DT-FC2. (E) The ROC of the classifiers constructed with RS-DT-FC3 (rs1169313, rs5082, rs9340799, rs10757274, rs1152002, Smoking, Hyperlipemia, HDL). (F) The PRC of the classifiers constructed with RS-DT-FC3.

Classifiers constructed with RS-DT-FC1, RS-DT-FC2 and RS-DT-FC3 had better performance compared to all of the other classifiers mentioned above. Therefore, RS-DT-FC1, RS-DT-FC2, and RS-DT-FC3 were considered the optimal FCs and were used to construct the nomograms described below.

Decision curve analysis helps clinical decision makers to balance the advantages and disadvantages of intervention and thus determine the best intervention point. It can also be used to evaluate whether a given model has practical value [24]. The decision curves for the logistic regression models constructed with RS-DT-FC1, RS-DT-FC2 and RS-DT-FC3 were distant from the baseline for a wide range of risk thresholds (Supplementary Fig. 2), suggesting that all of these models have high net benefits and potential practical value.

Nomogram is a graphic tool used for complex calculations. It can transform the logistic regression model into a simple and intuitive scoring system that has more practice value for clinicians [25]. Nomograms built using RS-DT-FC1, RS-DT-FC2 and RS-DT-FC3 (RS-DT-FC1-nom, RS-DT-FC2-nom and RS-DT-FC3-nom, respectively) show in graphic form the effect of each factor on the risk of PCAD (Fig. 6A,C,E). The calibration curves for the nomogram models showed good agreement between the predictions and actual observations (Fig. 6B,D,F). RS-DT-FC1-nom, RS-DT-FC2-nom and RS-DT-FC3-nom also showed good discrimination, with C-indexes of 0.79 (95% CI: 0.73, 0.86), 0.82 (95% CI: 0.76, 0.88) and 0.79 (95% CI: 0.72, 0.86) respectively for validation with the training dataset, and 0.94 (95% CI: 0.88, 1.0), 0.94 (95% CI: 0.85, 1.0) and 0.90 (95% CI: 0.82, 0.98) respectively for validation with the test dataset.

Fig. 6.

Nomogram and calibration curve. To use the nomograms in clinical practice, find the points corresponding to the variable value on the variable axis, draw a line vertically up to the points axis, read and record the score corresponding to each variable value, and sum the scores obtained. Then, find the points corresponding to the total score on the total points axis and draw a line straight down to the probability axis, and read the probability of PCAD. The arrow indicates the optimal cutpoints on the total points axis. If the individual’s total score is greater than the optimal cutpoints, it will be predicted high PCAD risk and marked as PCAD. On the category variable axis, ‘1’ indicates that the event represented by the variable name has occurred, and ‘0’ indicates that the event represented by the variable name has not occurred. The feature (variable) names are showed on the left of each nomogram. (A), (C) and (E) represent the nomograms constructed with RS-DT-FC1, RS-DT-FC2 and RS-DT-FC3, respectively. (B), (D) and (F) showed the calibration curve of the nomograms corresponding to (A), (C) and (E), respectively.

The optimal cutpoints for RS-DT-FC1-nom, RS-DT-FC2-nom and RS-DT-FC3-nom were computed using the R package ‘OptimalCutpoints’. These were 101.29, 27.74 and 186.01, respectively. Nomogram scores for each test sample were calculated using RS-DT-FC1-nom, RS-DT-FC2-nom and RS-DT-FC3-nom. If the total nomogram score for a sample was greater than or equal to the cutpoint for that nomogram model, it was predicted to be from a PCAD patient, otherwise it was predicted to be from a control. Samples in the test dataset were classified by comparing the total points, as calculated by reference to the nomograms, with the cutpoints. The results obtained using RS-DT-FC1-nom, RS-DT-FC2-nom and RS-DT-FC3-nom showed a prediction sensitivity of 0.92, 0.96 and 0.86, and an AUC of 0.89, 0.93 and 0.83, respectively (Supplementary Fig. 3).

Despite the high-performance classifiers and nomograms, this study has some limitations. Firstly, the data was from a single center and the sample size was relatively small. Secondly, this was a retrospective rather than a prospective study. Although the models could accurately classify individuals into PCAD and control groups, the predictive power of the models requires further validation in large prospective studies. This study also did not include other factors identified over the past 10 years and that may be linked to PCAD. Finally, the sample population was derived from a single race, thus limiting the universality of the models. Ideally, these models should be tested with larger samples and with different populations.