Academic Editor: Rafael Franco
Background: Machine learning techniques and magnetic resonance imaging methods have been widely used in computer-aided diagnosis and prognosis of severe brain diseases such as schizophrenia, Alzheimer, etc. Methods: In this paper, a regularized multi-task learning method for schizophrenia classification is proposed, and three MRI datasets of schizophrenia, collected from different data centers, are investigated. Firstly, slice extraction is used in image preprocessing. Then texture features of gray-level co-occurrence matrices are extracted from the above processed images. Finally, a p-norm regularized multi-task learning method is proposed to simultaneously learn the site-specific and site-shared features of the multi-site data, which can effectively discriminate schizophrenia patients from normal controls. Results: The classification error rate on 10 datasets can be reduced from 10% to 30%. Conclusions: The proposed method obtains excellent results and provides objective evidence for clinical diagnosis and treatment of schizophrenia.
According to the quantitative evaluation of the world health organization, brain diseases such as Alzheimer, Parkinson, and schizophrenia, etc. account for about 28% of all kinds of diseases in the world [1], which seriously threatens human health. Among them, schizophrenia is the most common psychosis. Its clinical manifestation is a syndrome with different symptoms involving many obstacles such as perception, thinking, emotion, behavior, as well as the disharmony of mental activities [2]. The diagnosis of schizophrenia in traditional medicine is mostly based on American DSM-IV, international ICD-10, and domestic classification and diagnostic criteria of mental disorders [3]. With the development of science and technology, various types of high-end medical imaging devices are developing rapidly. And medical images play an increasingly important role for assisting doctors to diagnose diseases. However, a large number of medical images have obviously increased the burden of doctors. At present, as a research hotspot in the field of medical science, image classification task is widely completed with the help of computer-aided means.
Among many medical images, magnetic resonance imaging (MRI) has been widely used in the clinical diagnosis of brain diseases due to its advantages of non-radiation and high resolution [4, 5]. A great deal of studies on sMRI show that abnormal gray matter located in multiple parts of the brain such as temporal lobe, parietal lobe and frontal lobe is the main manifestation of schizophrenia patients [6, 7]. In many papers, brain abnormalities in schizophrenia striatum [8, 9] and hypothalamus [10] have been identified. In paper [11] the gray matter texture analysis of magnetic resonance images is used, and it is determined that there is heterogeneity in the cerebral gray matter structure of schizophrenic patients. Therefore, abnormal sMRI images can be used to diagnose schizophrenia disease according to biological characteristics. In paper [12], a method called volume local binary patterns (VLBP) was used to calculate texture features to classify fMRI images of schizophrenic patients. In paper [13], the gray level co-occurrence matrix texture features of sMRI images combined with XGBoost were used to classify schizophrenia patients, which effectively verified the role of computer-aided diagnosis.
At present, based on MRI images of some brain diseases, researchers usually study image segmentation, recognition and classification in single area. However, in the era of internet information explosion, it is possible to obtain MRI images of multiple regions of homologous brain diseases through multiple channels. In the literature [14] multi-site data with 900 subjects was used, and about 200 subjects from 2 sites were included in the paper [15]. Papers [16, 17] show that, compared with a small number of samples in a single area, MRI data of the same kind of brain diseases in multiple sites can provide more sufficient statistical information, so as to better explore the functional mode of the brain structure of a patient. By studying the papers [18, 19, 20], it can be found that compared with the patients in a single area, the population distribution of the same disease in different regions is diverse. For example, there are certain differences in the structure and function of different people’s brains. The severity of the disease and the clinical symptoms in the population of multi-site are different. The type of patients is more extensive, etc. Obviously, studying the medical images of the same patients in many areas can not only get more comprehensive image information or a consistent pattern of abnormal pathological characteristics, but also analyze the characteristics of medical images in a single area. The experimental results are also more convincing. With the wide cooperation between international medical institutions and medical workers, it is an inevitable trend to study the pathological mechanism of the disease by using medical image data from multi-site of the sick people.
It can be seen from the above that, on the basis of multi-site MRI image data of schizophrenia brain disease, computer-aided diagnosis technology is used to distinguish normal and abnormal MRI images, and finally to correctly classify patients and normal people. The advantages are obvious. However, when any classifier is trained under limited sample conditions, it is difficult to replace the infinite sample pattern with a limited sample mode and to achieve a high degree of conformity with the actual pattern, especially under the conditions of the small number of MRI image sample and less diversity. Aiming at this problem, the advantage of multi-task learning method [21] is gradually presented. Multi-task learning is an optimal learning method by mining shared information among tasks while training multiple related tasks. It can significantly improve the learning effect of the algorithm, and has been applied to many fields such as spam filtering [22], natural image classification [23], various disease modeling, classification and prediction [24, 25] and so on. In the articles [26] and [27], using mutual inductive bias, multi-task learning can obtain bias information to supplement the lack of samples, which can simultaneously learn single task’s unique feature information and feature information shared by multiple tasks, and effectively improve the generalization ability of the model. Evgeniou et al. [28] proposed a regularized multi-task learning (rMTL) method based on support vector machine (SVM) model. This method added regularized penalty term which constrains the correlation parameters of different task model, and improves the generalization ability of the model. In the paper [29], a regularized multi-task learning method based on SVM and hybrid norm of and was proposed for MRI image classification of depressive disorders patients, and excellent results were obtained. The classification error rate on 10 datasets can be reduced from 10% to 30%.
Inspired by previous research, in this paper the classification problem of schizophrenia MRI images in multi-site data centers is regarded as a multi-task learning problem. A regularized multi-task learning classification model with SVM and p-norm is constructed, and the gradient descent method is used to optimize this model. Finally, this model is used to classify the MRI images of schizophrenic patients and normal people.
The rest of this paper is organized as follows. In section 2, the detail of the data is given, and the data preprocessing and statistical analysis is specified. In section 3, detailedly presents the proposed classification method is introduced. The experimental results and analyses are provided to demonstrate the feasibility and effectiveness of our method in section 4. In section 5, a conclusion is drawn.
MRI data were collected in the United States of America, Brazil, and China
(referring as site A, site B, and site C). 132 normal controls (NC) and 137
schizophrenia patients (SCZ) were recruited in site A, 94 NC and 62 SCZ in site
B, 181 NC and 144 SCZ in site C. All patients met DSM-IV [30] criteria and were
diagnosed as schizophrenia by psychiatrists. All the sMRI image scans were
acquired on a GE 3-T Signa scanner (GE Medical Systems, Milwaukee WI, USA) with
the following protocol: slice thickness = 1 mm, TE = 3.2 ms, TR = 8.2 ms, flip
angle = 12°, acquisition matrix = 256
The acquired MRI images were preprocessed using the statistical parametric mapping software package (SPM, Wellcome Trust Centre for Neuroimaging, Institute of Neurology, London, UK, http://www.fil.ion.ucl.ac.uk/spm) in which the following steps such as skull stripping, bias correction, tissue segmentation (four types of tissue including gray matter, white matter, cerebrospinal fluid, and lateral ventricles), spatial registration to a Montreal neurological institute (MNI) template, generation of the regional analysis of volumes examined in normalized space maps called RAVENS [31, 32] of gray matter, white matter, cerebrospinal fluid by the deformable registration package, named DRAMMS, which is publicly available [33], and the smoothing of RAVENS maps using a 6-mm full width at half maximum (FWHM) Gaussian filter are included.
To better illustrate the demographic and clinical characteristics of the study groups, the Student’s t-test of the age means and Pearson Chi-square test for gender differences were calculated. The statistical analysis of 200 subjects is analyzed in the Table 1.
| Region | Class | Sample size | Gender (male/female) | Average age/years | Age range/years |
| A | SCZ | 60 | 37/23 | 34.68 | 18 |
| NC | 60 | 28/32 | 31.78 | 13 | |
| p Value | – | 0.09 |
0.22 |
– | |
| B | SCZ | 60 | 44/16 | 27.53 | 18 |
| NC | 60 | 37/23 | 29.73 | 18 | |
| p Value | – | 0.17 |
0.13 |
– | |
| C | SCZ | 60 | 23/37 | 30.85 | 16 |
| NC | 60 | 28/32 | 33.93 | 20 | |
| p Value | – | 0.36 |
0.11 |
– | |
| A + B + C | SCZ | 180 | 105/75 | 31.39 | 16 |
| NC | 180 | 89/91 | 30.90 | 15 | |
| p Value | 0.09 |
0.65 |
– | ||
It can be seen from the Table 1 that these 200 subjects are matched in age and gender in dataset. And no statistically significant characteristic occurs when the difference p is smaller than 0.05.
Brain MRI data is typically stored in the form of three-dimension. In our study,
we investigate the gray matter image of structural magnetic resonance imaging
(sMRI) which has a size of 96
(1) Original images are sliced. For each subject, the size of gray matter image
is 96
(2) Sliced images are selected and converted to gray images. By removing 10 slices (the head most 5 slices and the backmost 5 slices) which don’t include feature information in the sliced gray matter images, and converting the remaining slices into gray images,the sequentially numbered slices are obtained and denoted as (i = 0, 1, 2 … 83). The part of sliced and grayed image slices of the first subject numbered NC001 are shown in Fig. 1.
 Fig. 1.
Fig. 1.Some examples of sliced gray matter images. From (a) to (h) they are respectively the 13th, 20th, 34th, 48th, 62nd, 69th, 76th, 83rd slices.
(3) The gray images are weighted and averaged. According to the structural integrity of the cerebral gray matter in each slice, the 84 slices were divided into three groups in sequence among which slices from 1st to 28th are a group. Similarly, slices from 29th to 56th and slices from 57th to 84th are respectively a group. Because the slices closer to the middle reflect more complete structure on the gray matter of the brain, they contain more feature information. And then the greater weight are given when calculating the average grayscale image. The equations for these three groups of images are described by
Img1, Img2, and Img3 are calculated using sMRI data of each subject after sMRI data is preprocessed, which puts a good way for the subsequent feature extraction.
Image feature extraction is a fundamental and critical step in medical image processing whose purpose is to show the characteristics or attributes of the samples in the form of numerical values, symbols and feature vectors. The results of feature extraction directly affect the classification accuracy. Because the texture information in the image is not sensitive to noise, light and color, the texture feature is chosen to use in this paper.
There is no universally mathematical model for texture feature extraction.
Because the gray-level co-occurrence matrix (GLCM) model method is not restricted
by the analysis object, it can well reflect the spatial gray distribution of the
image and the texture features of the image, and has been widely used [34]. GLCM
which describes the grayscale of adjacent pixels (or within a certain distance)
is a statistical matrix, and reflects the comprehensive information which
consists of the image gray change in the direction, interval, and amplitude.
Assume the gray level of a digital image is N, p (i, j)
represents the possibility (or frequency) of the appearance of grayscale
j under the condition that the starting grayscale is i, where
it is assumed that j is along the direction
(1) Mean:
The mean reflects the regularity of texture. The smaller the mean is, the more disorganized the texture is.
(2) Variance:
The variance measures the deviation of the pixel value from the mean. The larger the variance is, the more the change of gray scale is.
(3) Entropy:
Entropy is the measurement of information contained in an image. The greater the value of entropy is, the more complex the texture is.
(4) Contrast:
Contrast reflects the total amount of local gray scale changes in an image. The greater the contrast of an image is, the clearer the visual effect of this image is.
(5) Correlation:
The correlation is a measure of the linear relationship of the gray scale. The longer the extension of the gray value in a certain direction is, the greater the correlation is.
(6) Homogeneity:
Homogeneity is used to measure the uniformity of the local gray level of an image. The more homogeneous the local gray scale is, the greater the value is.
(7) Energy:
Energy is the measurement of uniformity of gray distribution in the image.
Using the above 7 kinds of texture features, a texture vector representing an image can be obtained.
The feature vectors need to be normalized so that any feature does not dominate among all of these features. All the feature vectors are normalized to contain zero mean and unit variance. The normalization is done by using the equation:
where
In summary, for each of these three weighted and averaged gray images (Img1, Img2, Img3), the above 7 statistics are calculated and normalized. Thus every subject can be represented using a vector containing 21 features.
Machine learning algorithm usually learns a task every time, and decomposes the complex problem into the theoretically independent sub-problems. Then it learns each sub-problem separately. Finally, it constructs the mathematical model of complex problems by combining the learning results of the sub-problems, namely single task learning [35, 36]. Multi-task learning is a machine learning method relative to single task learning. It uses information shared by multiple tasks to learn multiple tasks simultaneously, and solves multiple problems simultaneously. The obtained results interact with each other. Sharing information between tasks is the prerequisite for multi-task learning. On this basis, the training of multiple tasks can improve the overall generalization performance of the model. The main difference between multi-task learning and single task learning is that the training process of the model is different [31, 32]. In the training process of single task learning, each task is independent and does not affect each other. Its disadvantage is that it ignores the information contained in other tasks during the process of single task training. To some extent, the loss of relevant training information is caused, and this part of the lost information may be very useful for the training process. Nevertheless, the training of multi-task learning takes into account the correlation and useful information shared between tasks. At the same time it learns multiple tasks in parallel. The difference between the two training model is shown in the Fig. 2 below.
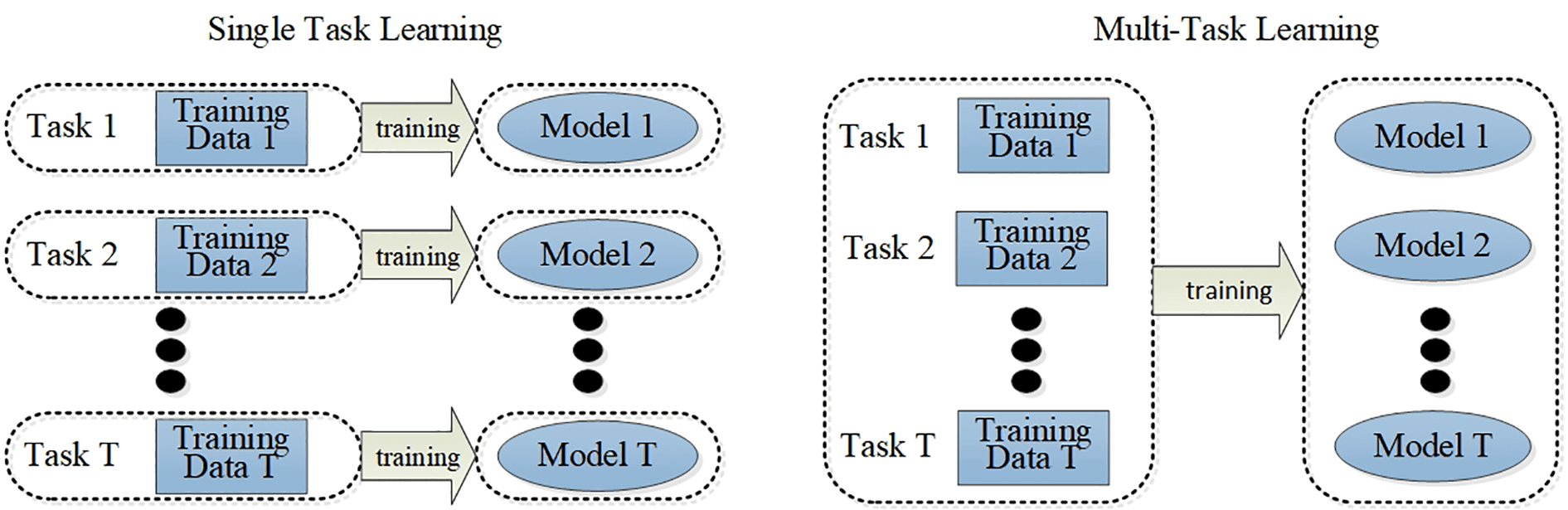 Fig. 2.
Fig. 2.The comparison of training process of single task learning model and multi-task learning model.
The most important issue of multi-task learning is how to build the model of relationship between tasks, and to make the relevant tasks share information. Finally, the goal of using the correlation between different tasks to improve the learning performance of the algorithm is achieved. We expect that the model fits the training data as much as possible, and is not too complicated at the same time. Therefore, the support vector machine algorithm with regularized multi-task is adopted to solve MRI image classification problems of mental illness in multi-site data centers.
Assuming that there are t supervised learning tasks in a multi-task learning
problem, for each task i, the learning function is assumed to be
where the first item is the empirical loss function on training data.
The optimal solution for a single t task is equivalent to the global problem of solving the target function of the joint t task, and is described by
The norm of the model parameter vector is usually used as regularized term in
machine learning. The regularization order needs to be set in advance.
where
where
Finally, the objective function of multi-task learning SVM with p-norm regularization is shown by
According to the different situation, the derivation of the Eqn. 17 is as follows.
If
If
The gradient descent method is used to update the
weight coefficient matrix
The experiments are elaborately designed and carried out using PC with Intel Core i5 (Intel Inc., CA, USA), CPU@2.40Ghz, speed 800 MHz, and 32G RAM. The compiling environments are Matlab2013a (American MathWorks company, MA, USA) and Python2.7 (Python Software Foundation, DE, USA).
In order to verify the effectiveness and robustness of the proposed method, comparative experiments are performed. (I) Single-site classification, i.e., that SVM classification algorithm was used to learn features of each single-site data separately for classification. (II) Pooling classification, i.e., that the three sites data were pooled together as a larger dataset regardless of the site differences. And SVM classifier was used to classify the remaining samples. (III) Multi-site classification, i.e., that SVM classification model with p-norm regularized multi-task learning was used to learn the site-specific and site-shared features simultaneously in the three data sites, and the two kinds of features were combined to classify the data corresponding to the data site.
In experiment (I), 72 cases were selected as training set from each site A, B, C, and the remaining samples serve as test sets. The feature vectors were input into the SVM classifier with the sigmoid kernel function. The main parameters include that penalty factor-c is 0.05, the fold of cross validation -v is selected 5 and 10, and the coefficient of kernel function -g is 0.05. The algorithm can be achieved through LIBSVM tools, and the performance of the classifier was evaluated by cross-validation. The classification accuracy was obtained at last. In experiment (II), 72 cases from each site A, B, C were selected for fusion, so a total of 216 cases are used as training set. The remaining samples of A, B, and C data centers were classified after the model was trained. Other experimental conditions were set in accordance with the experiment (I). In experiment (III), 72 cases were selected as training set from each site A, B, C, and the remaining samples serve as test sets. The feature vectors were input into the proposed support vector machine classifier with p-norm multi-task. Hinge function was selected as loss function of the model, and gradient descent method was used to solve optimization of objective function (15). The optimal value of each parameter was based on the principle in which only one variable is changed.In the experiment, Gaussian kernel function [37] was selected as the SVM kernel function. In the SVM classifier the penalty coefficient c is 20 and rbf [37] kernel parameter g is 1.2. For verifying the role of multiple texture features, local binary pattern (LBP) [38] features are used to fuse in series GLCM ones because of the their advantages such as simpleness, validity, and spectrum form.
The multi-task learning method was proposed to simultaneously learn the site-specific and site-shared features of the multi-site data. According to Eqns. 11,12,13,14,15,16,17 the gradient descent method is used to optimize the hinge loss function, and to verify the convergence of the proposed algorithm. As the number of iteration increases, the value of loss function shows a decreasing trend as shown in Fig. 3. It can be seen that the algorithm has good convergence property.
 Fig. 3.
Fig. 3.The proof of algorithm convergence.
The best classification accuracy (ACC) and area under receiver operating characteristics curves (AUC) obtained by each experiment are shown in the Table 2.
| Experimental method | A Site | B Site | C Site | ||||
| ACC | AUC | ACC | AUC | ACC | AUC | ||
| (I) | GLCM + 5 folds | 56.52% | 0.58 | 58.97% | 0.60 | 60.26% | 0.56 |
| GLCM + 10 folds | 57.02% | – | 59.14% | – | 60.22% | – | |
| GLCM + LBP + 5 folds | 58.33% | 0.59 | 60.42% | 0.65 | 62.50% | 0.58 | |
| GLCM + LBP + 10 folds | 57.69% | – | 60.46% | – | 61.84% | – | |
| (II) | GLCM + 5 folds | 60.00% | 0.65 | 67.60% | 0.70 | 69.00% | 0.62 |
| GLCM + 10 folds | 60.21% | – | 67.64% | – | 68.79% | – | |
| GLCM + LBP + 5 folds | 60.83% | 0.67 | 66.67% | 0.71 | 69.17% | 0.62 | |
| GLCM + LBP + 10 folds | 60.65% | – | 68.17% | – | 68.75% | – | |
| (III) | GLCM + 5 folds | 66.67% | 0.73 | 75.00% | 0.72 | 70.83% | 0.67 |
| GLCM + 10 folds | 68.70% | – | 76.30% | – | 72.83% | – | |
| GLCM + LBP + 5 folds | 68.75% | 0.76 | 77.08% | 0.73 | 72.92% | 0.70 | |
| GLCM + LBP + 10 folds | 68.55% | – | 77.25% | – | 72.67% | – | |
| GLCM, Gray-level Co-occurrence Matrix; LBP, Local Binary Pattern; ACC, Accuracy; AUC, Area Under Curv; A, United States of America; B, Brazil; C, China. | |||||||
It can be seen from Table 2 that, under the premise of using 5-fold cross-validation, the classification accurate rates of the three data centers (A, B, C) are 56.52%, 58.97%, and 60.26% respectively in the experiment of single task learning algorithm. In joint classification experiment, the classification accurate rates of the three data centers (A, B, C) are 60.00%, 67.60%, and 69.00% respectively. However, in multi-task learning classification experiment, the classification accuracy rates of the three data centers (A, B, C) can reach 66.67%, 75.00%, and 70.83% respectively. The AUC of the three data centers (A, B, C) are 0.73, 0.72, and 0.67 respectively. The results of joint classification have increased to some extent compared to single-task learning classification. But multi-task learning is clearly superior to single task learning classification results. The classification performance of the multi-task learning algorithm is better than single-task learning system in this experiment, because the multi-task learning process considers the association of multiple tasks. The model uses the shared information between tasks to enhance the inductive bias of the system, when training multiple tasks at the same time. Because the p-norm regularized term is added, the redundant features are effectively removed and the computational complexity of the model is reduced.
Furthermore, in order to verify the effectiveness of various features, we conduct experiments by merging LBP (Local Binary Pattern) and GLCM features in series. The experimental results show that effective fusion of multiple features such as LBP and GLCM can improve the classification accuracy to a certain extent.
Under the premise of using 10-fold cross-validation, the experimental results
did not show a significant improvement on accuracy. Sometimes the mean accuracy
even lower than the results of 5-fold cross validation. Actually, in
cross-validation, the choice of k value can refer to the empirical
formula which is k
In this paper, for discriminating schizophrenia patients from healthy controls, image processing and machine learning are introduced into the aided diagnosis and analysis of schizophrenia disease based on SMRI. Firstly, for achieving the effect of reducing dimension, the gray matter image is sliced, weighted and averaged preprocessing. Then GLCM texture features are extracted and normalized. Besides, the experimental samples are analyzed from the statistical point of view, excluding the influence of sex, age factors on the experimental results. At last, the main contribution of this work is that a support vector machine method with p-norm regularized multi-task learning is proposed and used to train and to establish the binary classification model. The experimental results show that multi-task learning approach has a superior performance compared with the single task learning method. It provides new ideas for studying multi-regional data and disease analysis. Furthermore, this experiment also provides guidance for computer-aided diagnosis and prognosis of mental illness. In the future work, more features will be considered to fuse, and the methods for mining deeper features of schizophrenia will be found, which can better improve the classification accuracy and assist doctors to diagnose schizophrenia disease.
These should be presented as follows: YW and HX designed the research study. JS performed the research. YW analyzed the data. YW and JS wrote the manuscript. All authors contributed to editorial changes in the manuscript. All authors read and approved the final manuscript.
Not applicable.
We thank the anonymous reviewers for their excellent criticism of the article.
This research was funded by Joint Project of Beijing Natural Science Foundation and Beijing Municipal Education Commission, grant number No. KZ202110011015.
The authors declare no conflict of interest.
Publisher’s Note: IMR Press stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
