1 Center for Adaptive Systems, Graduate Program in Cognitive and Neural Systems, Departments of Mathematics & Statistics, Psychological & Brain Sciences, and Biomedical Engineering, Boston University, 677 Beacon Street, Boston, 02215 MA, USA
Abstract
This article describes neural models of attention. Since attention is not a disembodied process, the article explains how brain processes of consciousness, learning, expectation, attention, resonance, and synchrony interact. These processes show how attention plays a critical role in dynamically stabilizing perceptual and cognitive learning throughout our lives. Classical concepts of object and spatial attention are replaced by mechanistically precise processes of prototype, boundary, and surface attention. Adaptive resonances trigger learning of bottom-up recognition categories and top-down expectations that help to classify our experiences, and focus prototype attention upon the patterns of critical features that predict behavioral success. These feature-category resonances also maintain the stability of these learned memories. Different types of resonances induce functionally distinct conscious experiences during seeing, hearing, feeling, and knowing that are described and explained, along with their different attentional and anatomical correlates within different parts of the cerebral cortex. All parts of the cerebral cortex are organized into layered circuits. Laminar computing models show how attention is embodied within a canonical laminar neocortical circuit design that integrates bottom-up filtering, horizontal grouping, and top-down attentive matching. Spatial and motor processes obey matching and learning laws that are computationally complementary to those obeyed by perceptual and cognitive processes. Their laws adapt to bodily changes throughout life, and do not support attention or conscious states.
Keywords
- Attention
- Learning
- Adaptive resonance theory
- Neural models
- Cognitive processing
- Neural networks
From our earliest years, parents and teachers may exhort us to “pay attention” to one or another important type of knowledge or event that we need to learn about, or action that we need to perform. Indeed, achieving success in life is quite unlikely unless one can pay attention to important tasks and valued goals for long periods of time. One just has to think about sports or the arts to realize this. The amount of sustained attention that is needed for a baseball player, ballet dancer, or virtuoso instrumentalist to achieve mastery is often spread over years, if not a lifetime, of effort. Even more mundane skills like learning to tie ones shoes or to drive a car take concerted attention over a period of days or weeks.
Many factors will determine how well we succeed in learning any of these skills. And understanding the central role of attention in achieving success is rendered difficult by the apparently intangible nature of this state of mind, seemingly so different from the vividness of seeing a friend’s face, hearing a favorite piece of music, knowing our own name, or feeling a warm rush of feeling when we see someone we love.
One reason why understanding how we pay attention is so difficult is that the act of paying attention is not separable from multiple other processes that are going on at any time in our brains, such as seeing, hearing, knowing, or feeling. Indeed, attention is an emergent property of interactions among thousands, or even millions, of neurons within brain networks and systems. Moreover, as I will explain below, mechanistically distinct types of attention occur in different brain systems. Separating them is made even more difficult by the fact that they can all interact synchronously together to enable us to experience a unified sense of self.
This article is devoted to providing accessible explanations of how, where, and why attention works in our brains. Such explanations are based on the mostly highly developed neural models of how our brains make our minds, including how we become conscious, and how consciousness is linked to our ability to pay attention. These models have been getting incrementally developed over the past 40 years. A self-contained and non-technical summary of brain models and how they may be combined to make our minds can be found in [1].
Other reviews of attention can be found in Wikipedia (https://en.wikipedia.org/wiki/Attention) and Scholarpedia (http://www.scholarpedia.org/article/Attention). These reviews describe observable psychological properties of attention, but not the mechanisms that cause them or the functions that these mechanisms carry out during behavior.
The current article explains how attention is integrated within interacting psychological and brain processes of Consciousness, Learning, Expectation, Attention, Resonance, and Synchrony (CLEARS). These processes, and how they interact, are explained below. The CLEARS processes have been modeled and simulated on the computer as part of Adaptive Resonance Theory (ART), which is the currently most advanced cognitive and neural theory of how our brains learn to attend, recognize, and predict objects and events in a changing world that is filled with unexpected events selfcontained and non-technical exposition of ART and other brain processes with which it interacts is found in the book [1]. Various articles include analyses of how normal and abnormal cognitive and emotional information processing, learning, recognition, memory, and consciousness interact [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 28, 40]; how sequences of objects and events are temporarily stored in cognitive or motor working memories before being chunked, or unitized, into learned sequence categories [21, 23, 31, 36, 39, 41]; how adaptively-timed reinforcement learning interacts with cognitive processes [22, 29, 30, 32, 33]; how visual grouping, attention, perception, and search interact with ART learning processes [25, 34, 35, 37, 38]; how auditory, speech, and language processes are clarified by ART dynamics [2, 24, 26]; how social cognition processes like gaze following and joint attention interact with ART dynamics [27]; and how ART may be used to design autonomous adaptive algorithms and robots for technology [20].
ART is not “just another” neural model. It has been derived from a Gedanken, or thought, experiment as the unique solution of the universal problem of how predictive errors can be autonomously corrected in a changing world [12]. The hypotheses from which the thought experiment is derived are, moreover, just a few familiar facts that we know from our daily lives. These facts are familiar because they are ubiquitous environmental constraints that have guided the evolution of our brains. When these hypotheses act together, as they regularly do in environments where individuals behave, they define a multiple constraint satisfaction problem that ART uniquely solves.
Grossberg ([12], p. 7) summarizes this evolutionary challenge as follows: “The importance of this issue becomes clear when we realize that erroneous cues can accidentally be incorporated into a code when our interactions with the environment are simple and will only become evident when our environmental expectations become more demanding. Even if our code perfectly matched a given environment, we would certainly make errors as the environment itself fluctuates”.
The thought experiment translates this purely logical inquiry about error correction into processes operating autonomously in real time with only locally computed quantities. The thought experiment thus shows how, when familiar environmental constraints on incremental knowledge discovery are overcome in a self-organizing manner through evolutionary selection processes, ART circuits naturally emerge. As a consequence, ART architectures may, in some form, be expected to be embodied in all future truly autonomous adaptive intelligent devices, whether biological or artificial.
Perhaps because of the fact that ART uniquely follows from the hypotheses of the thought experiment, all of the basic neural mechanisms that ART has proposed have been supported by psychological and neurobiological data. ART has also provided a unified explanation of hundreds of other experiments, and has also made scores of predictions that have subsequently received experimental support, as the above cited articles about ART illustrate.
ART is thus a principled biological theory of how our brains learn to attend, recognize, and predict objects and events in a changing world. It is not just an algorithm defined by feedforward adaptive connections with no top-down attentional mechanism, as it the case with many popular neural learning algorithms, including competitive learning, simulated annealing, Boltzmann Machine, back propagation, and Deep Learning.
In particular, back propagation and Deep Learning lack a mechanism for paying attention to predictive data and for dynamically stabilizing learning of it. As a result, neither back propagation nor Deep Learning is trustworthy—because neither is explainable—nor reliable—because each can experience catastrophic forgetting. Explainability means that the basis for making a prediction can be explicitly derived from the state of the algorithm. Catastrophic forgetting means that an arbitrary part of an algorithm’s learned memory can unpredictably collapse. Life-or-death decisions, including medical and financial decisions, cannot confidently be made using an algorithm with these weaknesses. Grossberg [42] explains why back propagation and Deep Learning have these deficiencies.
Many learning algorithms can be trained as classifiers, but do not have the unique combination of properties that ART embodies, including how attention helps to realize ART’s ability to realize autonomous adaptive intelligence in response to a changing world. This article summarizes how attention does this.
Back propagation became popular in the 1980’s after a publication by Rumelhart, Hinton, and Williams [43] applied earlier discoveries of scientists like Amari [44], Werbos [45, 46], and Parker [47, 48, 49]. Schmidhuber [50] provides an extensive historical summary of various contributions to the development of back propagation. It was soon, however, realized that back propagation suffers from many serious problems. For example, Grossberg [51] summarized 17 problems of back propagation which Adaptive Resonance Theory had already overcome starting in the 1970s. They are, listed as follows:
• Real-time (on-line) learning vs. lab-time (off-line) learning
• Learning in nonstationary unexpected world vs. in stationary controlled world
• Self-organized unsupervised or supervised learning vs. supervised learning
• Dynamically self-stabilize learning to arbitrarily many inputs vs. catastrophic forgetting
• Maintain plasticity forever vs. externally shut off learning when database gets too large
• Effective learning of arbitrary databases vs. statistical restrictions on learnable data
• Learn internal expectations vs. impose external cost functions
• Actively focus attention to selectively learn critical features vs. passive weight change
• Closing vs. opening the feedback loop between fast signaling and slower learning
• Top-down priming and selective processing vs. activation of all memory resources
• Match learning vs. mismatch learning: Avoiding the noise catastrophe
• Fast and slow learning vs. only slow learning: Avoiding the oscillation catastrophe
• Learning guided by hypothesis testing and memory search vs. passive weight change
• Direct access to globally best match vs. local minima
• Asynchronous learning vs. fixed duration learning: A cost of unstable slow learning
• Autonomous vigilance control vs. unchanging sensitivity during learning
• General-purpose self-organizing production system vs. passive adaptive filter
Several of the most serious problems will be discussed below.
Due to such problems, back propagation was gradually supplanted by other neural network algorithms. Although Deep Learning shares these problems with back propagation, it has become popular lately, largely because of the advent in the intervening years of huge online databases—which make it easier to train the algorithm using lots of data—and much faster computers-which facilitate the multiple learning trials that are needed because of the algorithm’s slow learning rate. Many tend like to think of Deep Learning as “back propagation on steroids”, since it has not solved the core foundational problems of its back propagation learning algorithm.
It is important to understand ART in an evolutionary context. The concept of “survival of the fittest” is often used to describe how Charles Darwin’s proposed evolutionary mechanism of natural selection works [52]. When applied to our brains, natural selection requires that “brain evolution needs to achieve behavioral success”, because it is only through behaviors that the cumulative effects of a species’ evolutionary specializations can be tested against the persistent challenges of changing environments.
Despite its status as the unique solution of the thought experiment about error correction using only locally computed quantities in a changing world, ART is just one of the biological neural network architectures that model how our brains make our minds. This is true because our brains need to solve many other problems than learning to attention, recognize, and predict objects and events in a changing world. The predictive ART, or pART, architecture embeds the core ART adaptive classification abilities within a more comprehensive brain macrocircuit of how human brains work (Fig. 1). Each of the processes in Fig. 1 have been developed as rigorous neural models, along with parametric simulations of many psychological and neurobiological data.
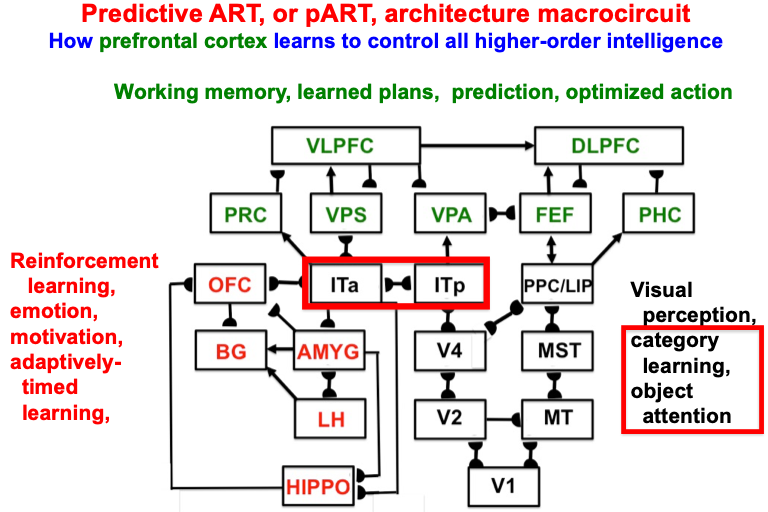 Fig. 1.
Fig. 1.The predictive ART, or pART, architecture unifies many of the brain processes that control biological intelligence. ART category learning and object (or prototype) attention processes take place in the model’s posterior inferotemporal cortex (ITp) and anterior inferotemporal cortex (ITa). The other brain regions and their processes are modelled by additional biological neural networks, whose abbreviations are printed with the same color (black, red, green) as the functions that they carry out. V1: striate, or primary, visual cortex; V2 and V4: areas of prestriate visual cortex; MT: middle temporal cortex; MST: medial superior temporal area; ITp: posterior inferotemporal cortex; ITa: anterior inferotemporal cortex; PPC: posterior parietal cortex; LIP: lateral intraparietal area; VPA: ventral prearcuate gyrus; FEF: frontal eye fields; PHC: parahippocampal cortex; DLPFC: dorsolateral hippocampal cortex; HIPPO: hippocampus; LH: lateral hypothalamus; BG: basal ganglia; AMGY: amygdala; OFC: orbitofrontal cortex; PRC: perirhinal cortex; VPS: ventral bank of the principal sulcus; VLPFC: ventrolateral prefrontal cortex. Output signals from the BG that regulate reinforcement learning and gating of multiple cortical areas are not shown. See Fig. 41 for some of these. Output signals from cortical areas to motor responses are also not shown. [Adapted with permission from [21] published in SAGE journals.]
The two inferotemporal cortical areas in pART—posterior inferotemporal cortex (ITp) and anterior inferotemporal cortex (ITa)—carry out ART-like attentive category learning. These cognitive networks receive preprocessed outputs from visual cortical areas in the lower right of the pART architecture—V1, V2, V4, MT, MST, PPC/LIP—that carry out the functionally distinct processes which together enable our brains to consciously see.
The macrocircuit in Fig. 2 summarizes key psychological processes that occur in different brain regions that interact within an emerging unified theory of visual intelligence. Note that these processes occur within both the ventral, or What, cortical processing stream and the dorsal, or Where, cortical processing stream (Fig. 3; [54, 55, 56, 57]), and interact using a combination of bottom-up, horizontal, and top-down interactions. It will be explained below how these top-down interactions embody distinct object and spatial attentional processes, and how and why paying conscious spatial attention to an object enables us to look at it and reach for it.
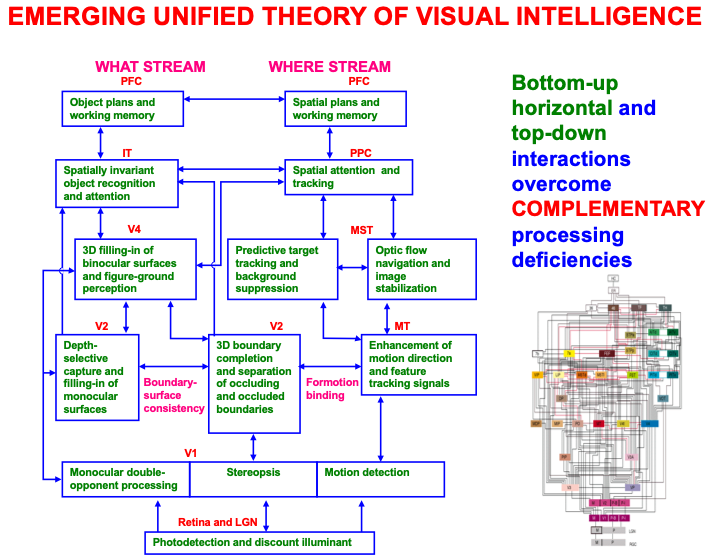 Fig. 2.
Fig. 2.A macrocircuit of some of the main brain regions and the processes that they carry out within and between the ventral, or What, cortical stream and dorsal, or Where cortical stream, that comprise an emerging neural model of biological vision. Bottom-up, horizontal, and top-down interactions among these regions overcome computationally complementary weaknesses that each process would exhibit if acted alone. [Reprinted with permission from [20] published in Elsevier.]
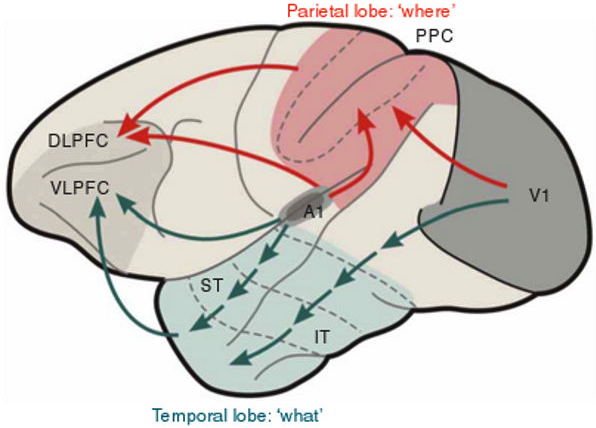 Fig. 3.
Fig. 3.What and Where cortical streams process inputs from both the visual and auditory modalities, with the What stream carrying out perception and recognition processes, and the Where stream carrying out spatial representation and action processes. V1: primary visual cortex; A1: primary auditory cortex; IT: inferotemporal cortex; ST: superior temporal cortex; PPC: posterior parietal cortex; VLPFC: ventrolateral prefrontal cortex; DLPFC: dorsolateral prefrontal cortex. [Reprinted with permission from [53] published in Nature Publishing Group.]
These models have been derived incrementally over the years using a modeling method and cycle that reflects the fact that brain evolution needs to achieve behavioral success, as summarized in Fig. 4.
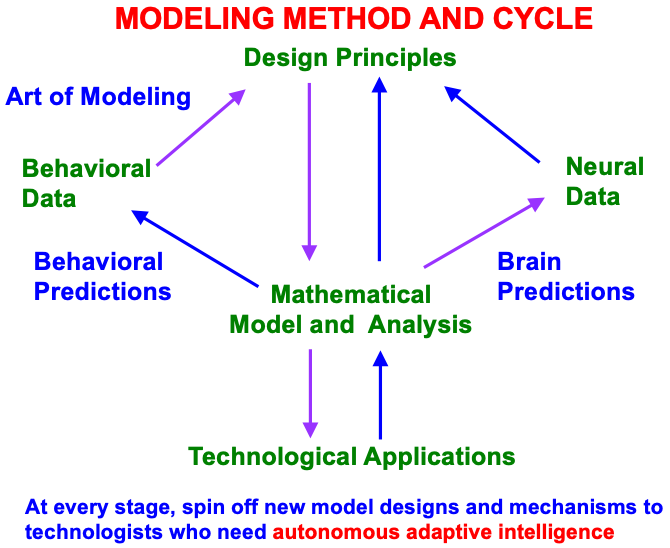 Fig. 4.
Fig. 4.Modeling method and cycle whereby to incrementally discover an increasingly comprehensive theory of how brain make minds, and to spin off new designs and mechanisms to engineers and technologists who are developing increasingly autonomous adaptive intelligent algorithms or robots. This Method of Minimal Anatomies begins by analyzing parametric data from scores or hundreds of behavioral experiments in a given topical area, and deriving from them design or organizational principles from which to define minimal mathematical models which embody the principles. Each minimal mathematical model can be interpreted as a neural network. At each stage of its derivation, this neural network explains much larger behavioral and neurobiological databases than were used to derive it, and explains how particular combinations of brain mechanisms interact to generate behavioral functions as emergent properties. The explanatory boundaries of each neural network call attention to design principles that have been omitted. Their inclusion permits the derivation of a neural network with a broader explanatory and predictive range. This cycle has continued through multiple iterations, leading to neural architectures, such as pART, which provide unified explanations of large interdisciplinary databases. [Reprinted with permission from [18] published in Frontiers.]
Below it will be shown how attention plays a key role in the ability of ART to support our behavioral success, and thus survival. ART top-down expectations enable humans to learn how to attend to those combinations of critical features which control actions that have led to behavioral success in the past (Fig. 5). These top-down learned expectations enable ART, and ourselves, to learn quickly and to remember what we have learned, often for many years, without experiencing catastrophic forgetting, or the unexpected collapse of part of our learned memories. Despite the persistence of these learned memories, they can also be forgotten, or extinguished, when they lead to unexpected consequences that disconfirm them.
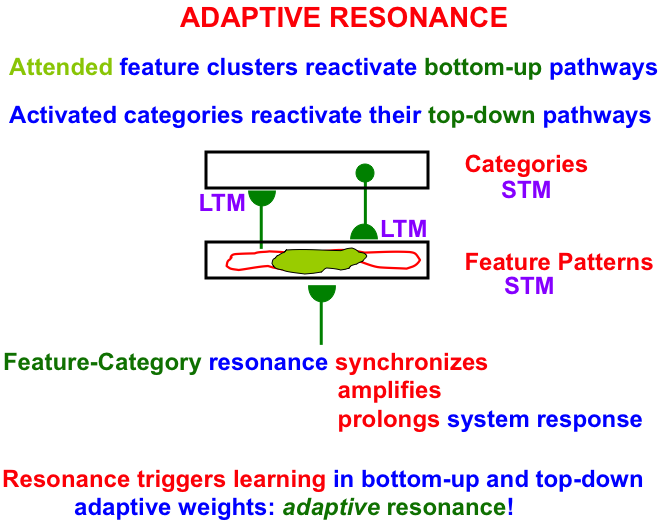 Fig. 5.
Fig. 5.A feature-category resonance binds together an attended critical feature pattern with the category that represents it. See the text for details. [Adapted with permission from [18] published in Frontiers.]
As Fig. 5 illustrates, an attended critical feature pattern across a level of feature detectors reactivates the bottom-up adaptive filter pathways that activate a level of learned recognition categories. The activated category, in turn, reactivates its top-down learned expectation signals. The positive feedback loop between features and categories gives rise to a feature-category resonance that synchronizes, amplifies, and prolongs the system’s response to the attended critical feature pattern and the category to which it is bound.
A feature-category resonance triggers fast learning in the adaptive weights, or long-term memory (LTM) traces, in the bottom-up and top-down pathways. Such an LTM trace learns a time-average of the critical feature patterns that are active when its pathway is active. More will be said about this learning law below.
A feature-category resonance also supports conscious recognition of the visual objects and scenes that it is processing at any given time. Table 1 summarizes a classification of different kinds of attentive resonances that occur across our brains, each of which supports a functionally different kind of conscious perception or recognition. These resonances illustrate the general prediction that “all conscious states are resonant stages” [12]. Multiple resonances typically synchronize with one another during daily experiences, so that we can consciously see, hear, know, and feel things about the world around us, thereby enabling the emergence of a unified self.

|
These resonances can synchronize because they share the same computational and functional units that are used within all parts of our brains, and can thus synchronously interact in a self-consistent manner (Table 2).
|
A small number of fundamental equations suffice to model all brain
functions, just as a small number of fundamental equations form the foundation of
all theoretical physics. These include equations for neuronal activation, also
called short-term memory, or STM, traces x
STM: Short-term Memory Shunting Model
MTM: Medium-term Memory
LTM: Gated Steepest Descent Learning and Memory
In Eqn. 1, the automatic gain control terms (B
The shunting dynamics in Eqn. 1 embody the membrane equations of neurophysiology operating in a recurrent on-center off-surround anatomy [62]. When the automatic gain control terms are removed, then the shunting STM equation reduces to the additive STM equation. The additive STM model cannot saturate, but it also does not have many of the valuable properties of the shunting model, including such essential properties for biological vision as the ability to discount the illuminant, or to compensate for huge changes in illumination that occur every day [63, 64].
The MTM Eqn. 2 describes how the chemical transmitter concentration at the
ends of the axons, or pathways, between neurons balances between a process of
accumulation H(K – y
The LTM Eqn. 3 describes how learning switches on and off when the
stimulus sampling signal f
With these STM, MTM, and LTM variables defined, it is possible to say that, when a feature-category resonance (Fig. 5) occurs between attended critical features and the recognition category to which they are bound by bottom-up and top-down excitatory signals, then fast learning is triggered in the adaptive weights, or long-term memory (LTM) traces, in the synaptic knobs at the ends of the bottom-up adaptive filter and top-down expectation axons (Table 1). Learning regulates the size of the adaptive weights, which regulate the amount of chemical transmitter that is released from synaptic knobs to the abutting nerve cell body, or change the sensitivity of postsynaptic membranes to these presynaptic signals, or both [65, 66, 67].
These equations are assembled within a somewhat larger number of modules, or microcircuits, that carry out different functions within each modality. They may be thought of as the “molecules” of biological intelligence. The modules include the following kinds of networks: shunting on-center off-surround networks, gated dipole opponent processing networks, associative learning networks, and adaptively timed spectral learning networks. Each type of module exhibits a rich set of useful computational properties, but are not general-purpose computers. Rather, each kind of module was shaped by evolution to carry out a range of different tasks that could be accomplished by specializations of its design.
For example, shunting on-center off-surround networks exhibit properties like contrast normalization, including discounting the illuminant during visual perception; contrast enhancement, noise suppression, and winner-take-all choice during the choice of a recognition category; short-term memory and working memory storage during the persistent short-term storage of individual events or sequences of events; attentive matching of bottom-up input patterns and top-down learned expectations, as occurs during a feature-category resonance; synchronous oscillations, as occurs during conscious resonances; and traveling waves that can occur during epileptic seizures.
These equations and modules are specialized and assembled into modal architectures. The term “modal” stands for different modalities of biological intelligence, including architectures for vision, audition, cognition, cognitive-emotional interactions, and sensory-motor control.
An integrated self is possible because it builds on a shared set of equations and modules within modal architectures that can interact seamlessly together.
Although they cannot compute everything, unlike a universal Turing machine or its hardware embodiment in a von Neumann computer (https://en.wikipedia.org/wiki/Von_Neumann_architecture), modal architectures are general-purpose in the sense that they can process all inputs to their modality, whether from the external world or from other modal architectures. Modal architectures are thus more general than a traditional AI algorithm. The types of resonances summarized in Table 3 form part of several different modal architectures, including modal architectures that enable conscious seeing, hearing, feeling, and knowing.

|
The exposition below will describe how the CLEARS processes interact within ART. Some of the psychological and neurobiological data for which ART has provided a unified explanation will be summarized, as well as ART predictions that not yet been tested experimentally.
Before moving on to these explanations, it is useful to note that ART properties such as fast learning without catastrophic forgetting, and learned selection by attention of the critical features that control effective decisions and predictions, have encouraged the mathematical analysis, computer simulation and application of multiple ART algorithms towards the solution of large-scale problems in engineering and technology. See http://techlab.bu.edu/resources/articles/C5.html, [68] and [69] for a partial list of applications, and the following articles for the mathematical and computational development of various ART algorithms [70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84].
For at least the past 40 years, the cognitive neuroscience literature has made the distinction between object attention [85] and spatial attention [86]. These Duncan and Posner articles included new experiments, but can be viewed as a further development of extensive earlier work by multiple authors. A small sample of early experiments includes those of Neiser [87], Lappin [88], and Treisman, Kahneman, and Burkeil [89] about object-based attention, often studied in displays that include multiple possible target and distractor objects. Early experiments probing spatial attention were carried out in alert monkeys [90, 91, 92], brain injured patients [93], and normal individuals [94].
The most compelling studies of object and spatial attention successfully dissociate paying attention to a single object at multiple positions, or to a single position inhabited by multiple objects (e.g., [95, 96, 97, 98, 99]). Although such studies represent an ideal that is possible to implement in the laboratory, in the real world, object attention and spatial attention often strongly interact, for example, when planning one’s escape from a predator in a forest. Such interactions have been the subject of hundreds of experiments which are often subsumed under the general rubric of visual search. Triesman and her colleagues interpret their data using their Feature Integration model (e.g., [100, 101, 102, 103, 104]), while Wolfe and his colleagues do so using variants of their Guided Search model (e.g., [105, 106, 107, 108, 109, 110]).
Biological neural network models have provided unified mechanistic explanations of many of the most challenging data about visual search (e.g., [7, 22, 37, 111]). These models of perceptual and cognitive information processing had previously been used to explain and predict other kinds of psychological and neurobiological data. Visual search data were hereby integrated within a broad landscape of experimental paradigms probing different aspects of how brains make minds.
For example, the Spatial Object Search, or SOS, model of Grossberg, Mingolla, and Ross [112] has the title “A neural theory of attentive visual search: Interactions of boundary, surface, spatial, and object representations”. The SOS model explains and simulates visual search data as emergent properties of interactions between visual perception processes of boundary completion and surface filling-in, object attention processes whereby ART categories are learned and recognized, and spatial attention processes whereby attention shifts to objects in different locations.
Interactions between object attention and spatial attention have been probed in the laboratory when, for example, they are sequentially primed by object or spatial cues during relatively brief time intervals. Theeuwes, Mathot, and Grainger [113] discuss such interactions in the context of “exogenously controlled object attention”, and review related studies by other authors. Exogenous control refers to bids for attention from the external world, whereas endogenous control refers to top-down attentional processes within our brains.
An exogenous attention shift to a location in space may be caused by the sudden appearance of an object in a scene [114, 115]. This automatic exogenous allocation of spatial attention can compete with endogenous top-down object attentional priming, thereby illustrating competition for attentional resources across the Where and What cortical streams. For example, if an observer is primed to look for a color singleton, then an abrupt onset of an object at a different position will cause an attentional shift that slows down search for the color singleton [114, 116].
Posner [86] emphasized this orienting process, as illustrated by the title of his article, “Orienting of attention”. The examples proposed by Posner [86] and Theeuwes et al. [113] describe an orienting response due to transient appearances of objects at different positions. As I will explain below, orienting can also be driven endogenously during an ART search, or hypothesis testing, for the internal representation of any event, whether or not it occurs along with a shift of spatial attention.
As noted by Theeuwes, Mathot, and Grainger [113], Posner and Cohen [117] studied exogenous attention shifts in an experimental setup where subjects fixate a central position surrounded by a regular array of outline boxes. Then one of two peripheral boxes is cued by brightening, before a target is presented inside a box. Participants detected the target faster when it appeared at the cued, relative to the uncued, box, thereby illustrating how a shift in spatial attention can facilitate object processing and attention at the cued position. It was also shown that this facilitation is coded in retinotopic coordinates.
Several labs have proposed that abrupt onsets capture attention by strongly activating transient cells that are designed to respond to rapid cue changes. These cells are abundant in the Where cortical stream that is also often referred to as the magnocellular pathway (e.g., [118, 119, 120, 121]) due to its abundance of retinal Y cells that are insensitive to object form and color blind, but highly sensitive to luminance transients and motion [122, 123, 124, 125, 126].
A detailed psychological, anatomical, and neurophysiological model has been incrementally developed to explain how transient cells, among many others, contribute to our brain’s ability to compute the direction and speed of objects that are moving within a cluttered environment that also contains many moving environmental distractors. This 3D FORMOTION model (Fig. 6) integrates form and motion information across multiple brain regions of the What and Where cortical streams, including cortical areas V1, V2, V4, MT, and MST (Fig. 7), to accomplish this feat.
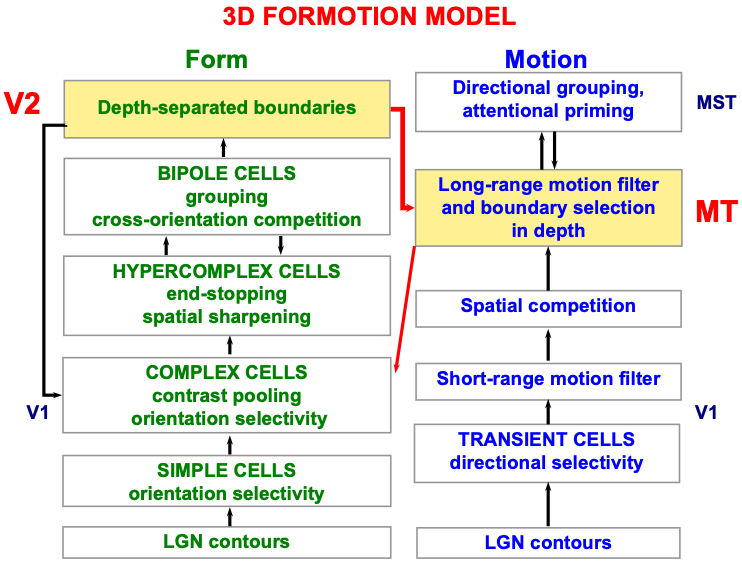 Fig. 6.
Fig. 6.Macrocircuit of the 3D FORMOTION model for form-to-motion, or FORMOTION, interactions from cortical area V2 in the What cortical stream to cortical area MT in the Where cortical stream. This interaction enables an observer to track a moving form in depth. See the text for details. [Adapted with permission from [127] published in Brill.]
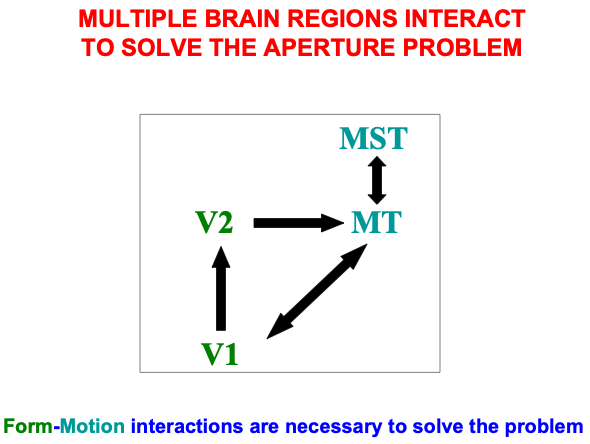 Fig. 7.
Fig. 7.Cortical regions and their bidirectional or cyclic interactions that carry out form-to-motion, or FORMOTION interactions. [Adapted with permission from [128] published in Elsevier.]
The 3D FORMOTION does so by developing a rigorous computational solution of the global aperture problem whereby our brains convert the ambiguous hodgepodge of local motion signals arriving at our retinas from the environment into coherent cortical representations of object motion direction and speed (e.g., [128, 129, 130, 131, 132, 133, 134, 135]).
As illustrated by Fig. 8, when an object moves under real world conditions, such as a leopard running across a grassy field, only a small subset of its image features, notably its bounding contours, may generate motion direction cues that accurately describe its direction-of-motion. The movements of the leopard’s limbs as it runs (red arrows) occur in multiple directions other than the direction that the leopard is moving (green arrows). The same is true of the contours of the spots on the leopard’s coat as they move with the limbs. Most local motion signals differ from the direction of object motion because they are computed from local views of object motion within neurons’ finite receptive fields.
 Fig. 8.
Fig. 8.The aperture problem arises because of two related limitations individual neuron’s receptive fields to compute the true motion direction of an object. One limitation arises because a line moving in any direction within a circular aperture appears to move in the direction that is perpendicular to its orientation. Another limitation arises because the motion direction of a moving object often differs from the directions in which its parts move. The 3D FORMOTION model solves the aperture problem. See the text for details. [Reprinted with permission from [1] published in Oxford University Press.]
The right insert in Fig. 8 illustrates the insight of Hans Wallach in 1935 [136] that the motion direction of a line seen within a circular aperture is perceptually ambiguous. No matter what the line’s real direction of motion may be, its perceived direction is perpendicular to its orientation. This phenomenon was called the aperture problem by Marr and Ullman [137]. The aperture problem is faced by any localized neural motion sensor, such as a neuron in the early visual pathway, that responds to a moving local contour through an aperture-like receptive field.
Until the aperture problem is solved, our brains cannot compute an object’s direction and speed of motion, and thus cannot localize spatial attention to track the object. The microcircuit in Fig. 6 of the 3D FORMOTION model shows that the model’s cortical area MST can control top-down attention upon the object motion direction and speed representation that is computed in cortical area MT. As described in [127] and [1], this attentional circuit obeys the same ART Matching Rule that is realized in all object attentional circuits, and which also supports learning and stable memory of the directionally tuned cells that enable leopards, and humans, to solve the aperture problem. Berzhanskaya, Grossberg, and Mingolla [127] also describe and explain many other data about object motion perception, including the coordinates in which it is computed. The ART Matching Rule will be explained in greater detail below.
Interactions between the form and motion streams are needed because the laws of form and motion processing are computationally complementary. As shown in Fig. 9, form processing within the What cortical stream areas of V1, V2, and V4 is orientationally sensitive, whereas motion processing within the Where cortical stream areas of V1, MT, and MST is directionally sensitive. Positionally and orientationally precise binocular matches between our two eyes (see left image) enable us to compute fine estimates of an object’s depth. In contrast, to compute an object’s motion direction, motion signals need to be pooled from multiple boundaries of the object with possibly different orientations (see right image). Such pooling cannot be done during a binocular estimate of depth. Hence fine depth estimates coexist with coarse direction estimates within the What stream. Because pooling across orientations must be done to derive a fine direction estimate, the Where stream can only compute a coarse depth estimate.
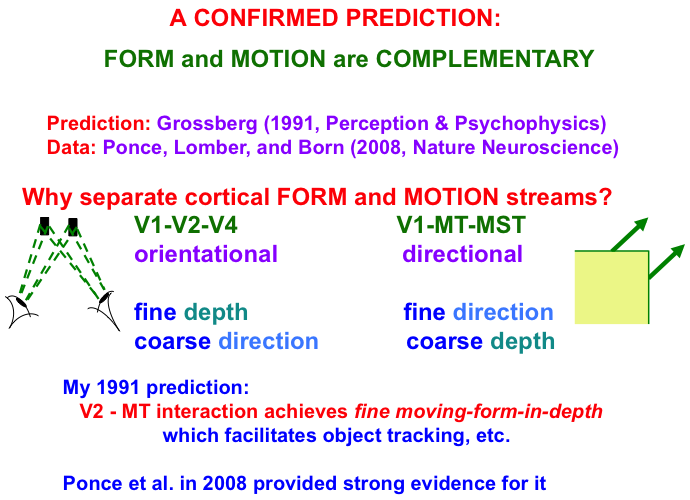 Fig. 9.
Fig. 9.Form and motion computations are complementary: The form
stream binocularly matches features that the two eyes receive from a nearby
object to compute an estimate of the object’s depth with respect to the observer.
Each binocular match occurs between left eye and right eye representations of the
same object feature in the world (see left image). These features thus represent
the same object orientation in the world, thereby enabling a
fine depth estimate to be computed. Restricting matches to the same
orientation, however, enables them to compute only coarse direction
estimates of object motion direction. The motion stream generates fine
direction estimates of an object’s motion by pooling over the object’s
differently oriented contours that are moving in the same direction (see right
image). Pooling over orientation enables only coarse depth estimates of
the object. FORMOTION interactions from V2-to-MT enable cells in MT to overcome
these complementary weaknesses to compute fine moving-form-in-depth,
which can be used to support accurate object tracking. If V2 is cooled, then only coarse depth estimates are recorded in MT, even
though fine estimates of motion direction are unimpaired.
Note: Prediction: Grossberg [34]. Data: Ponce, Lomber, and Born [139].
Fig. 10 summarizes one of many demonstrations that computations of form and motion are, in fact, orientationally and directionally sensitive, respectively. The left half of the figure describes the Mackay illusion: Inspect intersecting lines before looking at a black wall or screen, where an afterimage of nested circles can be seen. The two images differ by 90 degrees. The right half of the figure describes the waterfall illusion: Inspect downward motion before looking at a black wall or screen, where an afterimage of upward motion can be seen. The two images differ by 180 degrees. These different symmetries for orientational vs. directional processing make clear that different brain systems support form and motion perception.
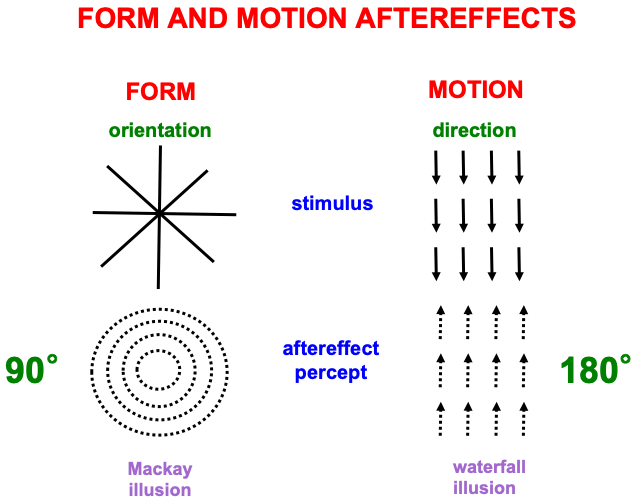 Fig. 10.
Fig. 10.Aftereffects of form and motion processing exhibit different asymmetries, with 90 degree differences between stimulus and aftereffect in the form stream, and 180 degree differences between stimulus and aftereffect in the motion stream. See the text for details. [Reprinted with permission from [1] published in Oxford University Press.]
Form-to-motion interactions from V2-to-MT overcome the complementary weaknesses described in Fig. 9 to compute fine moving-form-in-depth estimates in MT (Fig. 11). This representation can then serve as a basis for attentively tracking a moving object, such as a predator or prey, in MST and beyond. I made this prediction in 1991 [138]. As Fig. 9 notes, Ponce, Lomber, and Born [139] confirmed my prediction in 2008 by reversibly cooling V2 and showing the predicted properties of fine direction and coarse depth estimates by MT cell responses, which returned to fine direction and fine depth estimates by MT responses after V2 recovered from cooling.
 Fig. 11.
Fig. 11.Summary of the complementary weaknesses of form and motion cortical computations that are overcome by FORMOTION interactions from V2-to-MT.
Once our brains overcome the aperture problem to compute reliable estimates of object motion, this information is used to support two different kinds of visually-guided navigational behaviors: object tracking and navigation. Object tracking enables us to track a target that is moving relative to us. A moving target can even be tracked behind multiple occluders, as could occur when a predator is tracking a moving prey that is intermittently occluded by bushes and trees in the forest. The predator can complete a continuous trajectory of the prey’s motion, even behind the occluders, using long-range apparent motion [130], which also maintains spatial attention upon the location that is currently most active in the trajectory.
Navigation enables us to move relative to the world around us. Fig. 12
summarizes the macrocircuit of the Visual Steering, Tracking, And Route
Selection, or ViSTARS, neural model of navigation [140, 141, 142]. The model shows that
object tracking and optic flow navigation are carried out by two parallel
cortical streams within cortical areas MT and MST (Fig. 7), with the ventral
stream MT
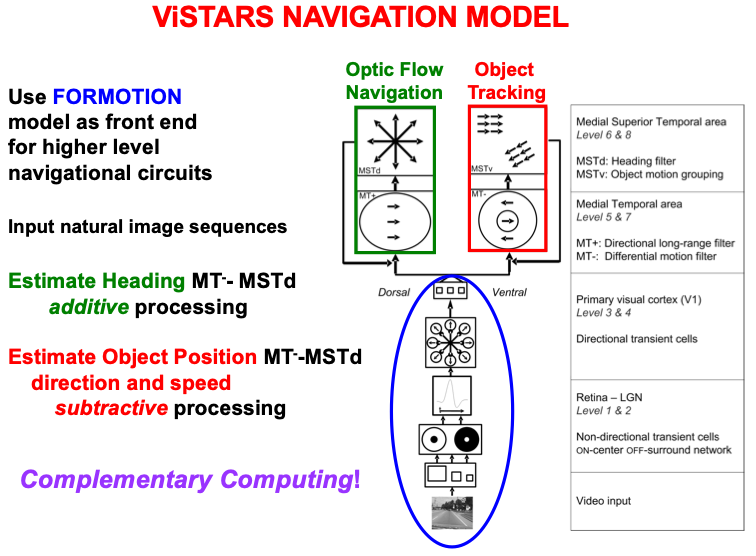 Fig. 12.
Fig. 12.The computation of heading during optic flow navigation, and of object position, direction, and speed during object tracking, obey computationally complementary laws. The ViSTARS model explains these different computations and the functions that they accomplish. See the text for details. [Adapted with permission from [140] published in Elsevier.]
Fig. 12 notes that these two parallel processing streams use computationally complementary processes: Additive processing enables the brain to determine the direction of heading, or a navigator’s self-motion direction, whereas subtractive processing is used to determine the position, direction, and speed of a moving object. These complementary types of processing enable the computation of an observer’s heading while moving relative to a scene, and of an object’s movements relative to the observer. This latter information can, in turn, be used to avoid collisions with objects in a scene while moving through it. Both processes contribute to an observer’s ability to lock attention onto a valued goal object and to maintain it while navigating towards that object.
The complementary laws of tracking and navigation are just one of many examples of the general principle of Complementary Computing that organizes how multiple pairs of interacting brain regions are specialized. Table 3 lists some pairs of psychological processes, and the cortical areas within which they occur, for which neural models have articulated computationally complementary properties.
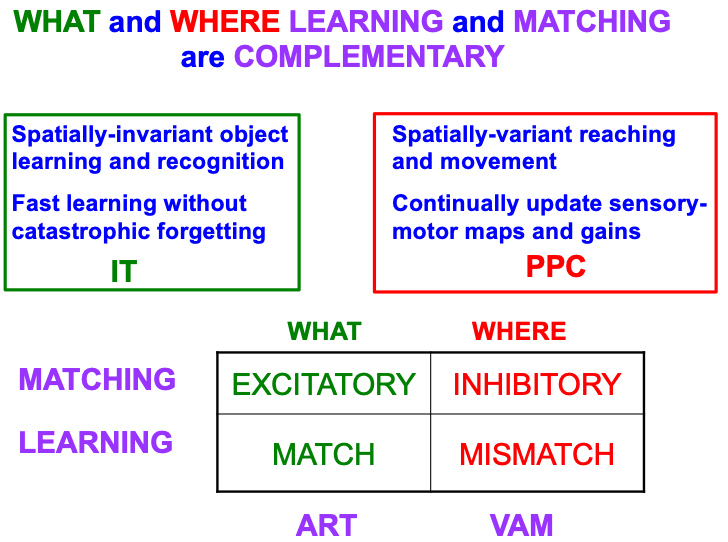
Table 4 summarizes complementary properties of learning and matching within the What and Where cortical streams. The What stream learns invariant object recognition categories within the anterior inferotemporal cortex, or ITa (Fig. 1). This learning can occur quickly without causing catastrophic forgetting. A single invariant object category can recognize multiple views of an object at different positions and image sizes on the retina. The ability of an invariant category to recognize an object that is seen at different positions is the spatially-invariant property that is summarized in the figure, in order to contrast it with the spatially-variant allocation of spatial attention in the posterior parietal cortex, or PPC, to control reaching and other movements towards different positions in space. As our limbs change in size and strength over the years, the circuits that control them can continually update their motor maps and gains—that is, can experience “catastrophic forgetting”—to ensure skillful performance.
|
The bottom part of Table 4 contrasts the computationally complementary mechanisms of matching and learning in the What and Where streams that generate these distinct learning and behavioral properties. As in the case of object tracking and navigation, invariant category learning and movement control differ by obeying excitatory vs. inhibitory laws, in this case matching laws. The category learning properties have been modeled by ART, some of whose foundational properties will be reviewed below, including how ART learning occurs when there is a good enough match between bottom-up input patterns and top-down learned expectation signals that focus object attention upon the critical features that predict successful decisions and actions. Such a match is excitatory because it initiates an attentive resonance which triggers category learning. It is thus an adaptive resonance, hence the name of ART.
The movement control properties have been modeled by Vector Associative Map, or VAM, dynamics [143, 144]. Unlike the excitatory matching and match-based learning of ART, a VAM model carries out mismatch-based learning that is used to calibrate its inhibitory matching computations, as when an arm’s present position is subtracted from a desired target position to compute a difference vector that controls the direction and distance of a reaching movement to the target. VAM dynamics will not be further discussed herein, except to note that, because of its inhibitory matching dynamics, VAM models cannot pay attention or become conscious.
The heuristic concepts of object and spatial attention can be refined in terms of the brain mechanisms that carry out these attentional processes. Object attention is replaced by the concept of prototype attention during recognition learning. As will be discussed more fully below, each active category in an ART architecture reads-out a top-down expectation which learns a prototype that encodes a time-average of the critical feature patterns that are attended when the category is active. This critical feature pattern also chooses the active category via its bottom-up adaptive filter signals to the category level. All of these operations occur within the What cortical stream.
The heuristic concept of spatial attention is replaced by the mechanistically more precise concepts of boundary attention and surface attention during visual perception. One reason that boundaries and surfaces are so important in spatial attention is that they are, when properly understood in terms of the processes of boundary completion and surface filling-in, the functional units of visual perception [112, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165].
Boundaries and surfaces are computed in the What cortical stream within visual cortical areas such as V1, V2, and V4 (Fig. 2). Boundaries and surfaces are another example of computationally complementary processes (Table 3). These complementary properties are summarized in Fig. 13, and are illustrated by the boundary completion and surface filling-in processes that occur during the visual illusion of neon color spreading.
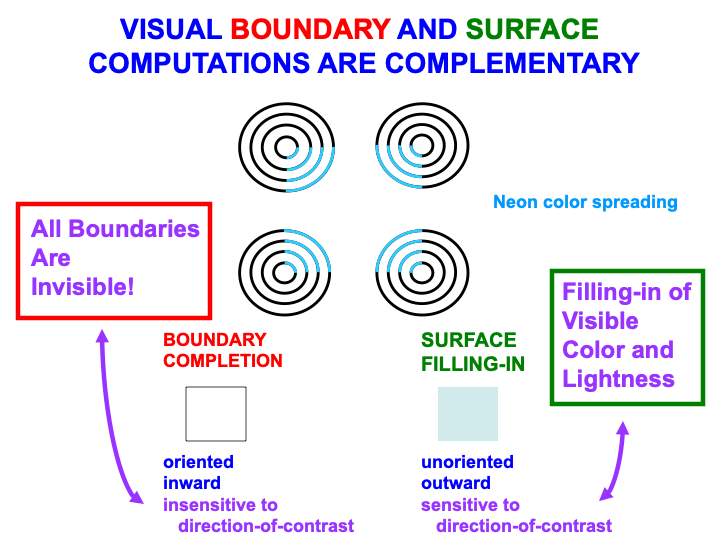 Fig. 13.
Fig. 13.Visual boundary and surface laws are complementary. [Adapted with permission from [166] published in Elsevier.]
Boundary completion and surface filling-in compensate for gaps and uncertainties that exist in retinal images due to the existence of a blind spot, retinal veins, light scattering within the retina, and other image-degrading processes. The blind spot is as large as the region of maximal retinal sensitivity to light, the fovea, yet we are not aware of it. Partly this is because the retina jiggles rapidly in its orbit, thereby creating transient signals from external objects due to their motion relative to the retina. These transients refresh the signals from external objects at the retina. The blind spot and retinal veins do not create transients because they are attached to the retina, hence they fade from visibility.
The result is an incomplete representation of the external world where the blind spot and veins have occluded it (Fig. 14, top image). Boundary completion and surface filling-in complete visual representations over the occluded regions (Fig. 14, bottom three images).
 Fig. 14.
Fig. 14.After retinal occlusions such as the blind spot and retinal veins fade because they do not generate transient refresh signals on the retina, boundary completion and surface filling-in restore visual representations over the occluded retinal regions. [Reprinted with permission from [23] published in Springer.]
It requires multiple processing stages in the visual cortex to create complete, context-sensitive, and stable cortical representations of visual boundaries and surfaces. I call this process hierarchical resolution of uncertainty. Hierarchical resolutions of uncertainty are needed in multiple brain processes to generate sufficiently complete representations of sensory data upon which to base successful actions.
The processing stage where perceptual representations are completed needs to be distinguished from the previous processing stages so that the complete representation can be used to control successful goal-oriented actions. Actions based upon incomplete representations could cause serious problems. The selected processing stage resonates with the subsequent one in the cortical hierarchy to selectively “light up” the complete representation. The lighting-up process renders the complete representation conscious so it can be used to guide successful actions. In this sense, we consciously see in order to look and reach, hear to communicate and speak, and feel to control effective goal-oriented actions (Table 5).

|
Spatial attention plays a major role in lighting up such a complete representation. It does so, in particular, by resonating with the object’s completed—notably, filled-in—surface representation. It is in cortical area V4 that such a completed surface representation is computed, thereby triggering a resonance with the posterior parietal cortex, or PPC.
This V4-to-PPC-to V4 resonating feedback loop is called a surface-shroud resonance (Fig. 15) because surface attention in PPC fits its shape to that of the surface with which it is resonating. Form-fitting spatial attention was called an attentional shroud by Tyler and Kontsevich [169].
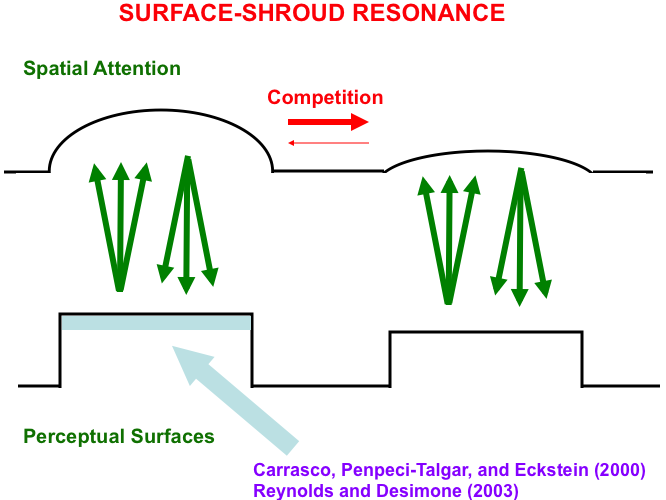 Fig. 15.
Fig. 15.A surface-shroud resonance between cortical areas
V4 and PPC lights up the complete surface representation that can be used to
control effective looking and reaching, as it focuses surface attention upon that
surface representation, and thereby increases its effective contrast (light blue
region). This enhancement has been reported in both psychophysical experiments
(e.g., [167]) and neurophysiological
experiments (e.g., [168]). [Reprinted with
permission from [19] published in Springer.]
Note: Carrasco, Penpeci-Talgar, and Eckstein [167]. Reynolds and Desimone [168].
Just as a feature-category resonance supports conscious recognition of a visual object or scene, a surface-shroud resonance supports conscious seeing of an object’s visual qualia (Table 1). When a feature-category resonance synchronizes with a surface-shroud resonance, our brain knows what a familiar object is as we see it, and are then also ready to reach it via the active surface representation in PPC (Fig. 16). The top-down feedback from PPC to V4 carries out surface attention even while the bottom-up signals from PPC to downstream movement circuits embody the intention to move to the attended location (e.g., [170, 171, 172, 173, 174]). Boundary-shroud resonances can, in a similar way, become conscious and control reaches to an object’s contours.
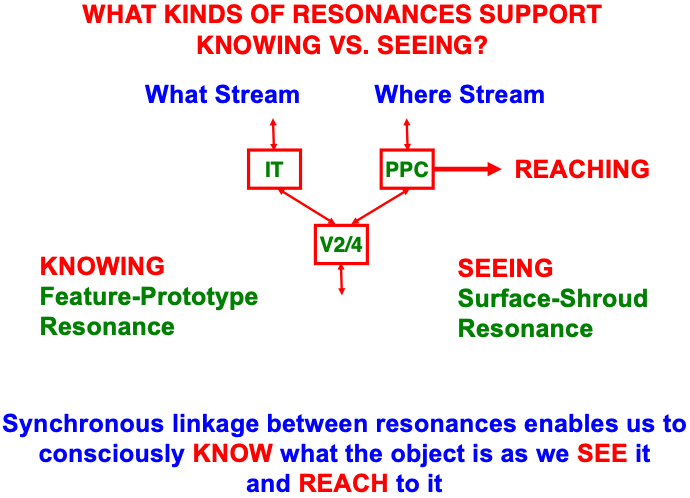 Fig. 16.
Fig. 16.A surface-shroud resonance that supports conscious seeing can synchronize with a feature-category resonance that supports conscious knowing, or recognition (see Table 1), so that we can both see and know a familiar object when we attend it. The position of the attended object in PPC can then be used to look at or reach it. [Adapted with permission from [19] published in Springer.]
When a lesion in the feature-category resonance pathway occurs, then visual agnosia results during which humans, and the model, can reach to a target without knowing what it is, as in the patient DF reported by Goodale et al. [55]. Properties of surface-shroud resonances have been used to explain challenging data both about visual perception in normal humans and defects of consciousness in clinical patients. Here I will just note that normal properties such as limited capacity of attention, perceptual crowding, change blindness, and motion-induced blindness, and clinical properties of visual and auditory neglect, all get a unified explanation in [19], which also provides references to the relevant experimental literature.
For example, in response to a hemifield lesion of parietal cortex, the model explains many properties of the visual or auditory neglect that ensues. Explained clinical data go considerably beyond the familiar facts that such individuals may omit drawing parts of a scene, or neglect to dress the side of the body, that the lesioned hemifield would have processed. In all these cases, the visual cortex is intact but, without the parietal cortex to support a surface-shroud resonance, conscious seeing of, and spatial attention to, the afflicted hemifield does not occur.
The above text has reviewed four examples of pairs of interacting processing streams in our brains that exhibit computationally complementary properties; namely, the first four processing pairs that are listed in Table 1. The processes in Table 1 are only a partial list of known computationally complementary processes in our brains. All of these processes need multiple processing stages to carry out a hierarchical resolution of uncertainty, and thus also require that completed representations be “lit up” by conscious resonances. I will show in the next sections that ART circuits also exhibit complementary properties. Complementary Computing has hereby emerged, from results of multiple modeling studies over the years, as a basic principle of how brain systems are specialized, yet strongly interact (Fig. 17).
 Fig. 17.
Fig. 17.Complementary computing requires new principles of uncertainty and complementarity, including the need for a hierarchical resolution of uncertainty, which clarify why multiple processing streams with multiple processing stages exist in our brains, as illustrated by the famous macrocircuit diagram of the visual system in the lower right corner that is adapted with permission from [175]. [Reprinted with permission from [20] published in Elsevier.]
With this background about prototype, surface, and boundary attention in hand, it is easier to mechanistically explain data about interactions between them. The experiments of Brown and Denny [176] are particularly illuminating in this regard.
Explaining data of this kind is possible using the ARTSCAN model of Fazl, Grossberg, and Mingolla [7] and its extension to the ARTSCAN Search model of Chang, Grossberg, and Cao [5], whose macrocircuit is summarized in Figs. 18 and 19. Perhaps the most important computational property of these models is that they enable autonomous incremental learning of invariant object categories. Fig. 18 describes interactions that support learning and naming of invariant object categories. Interactions between surface and boundary attention in the Where cortical stream, and prototype attention in the What cortical stream, coordinate these learning, recognition, and naming processes. Fig. 19 describes the model processes that can direct a search for a previously learned, and currently desired, target object in a scene, thereby clarifying how our brains solve the Where’s Waldo problem. More about how invariant object categories are learned will be said in the following section.
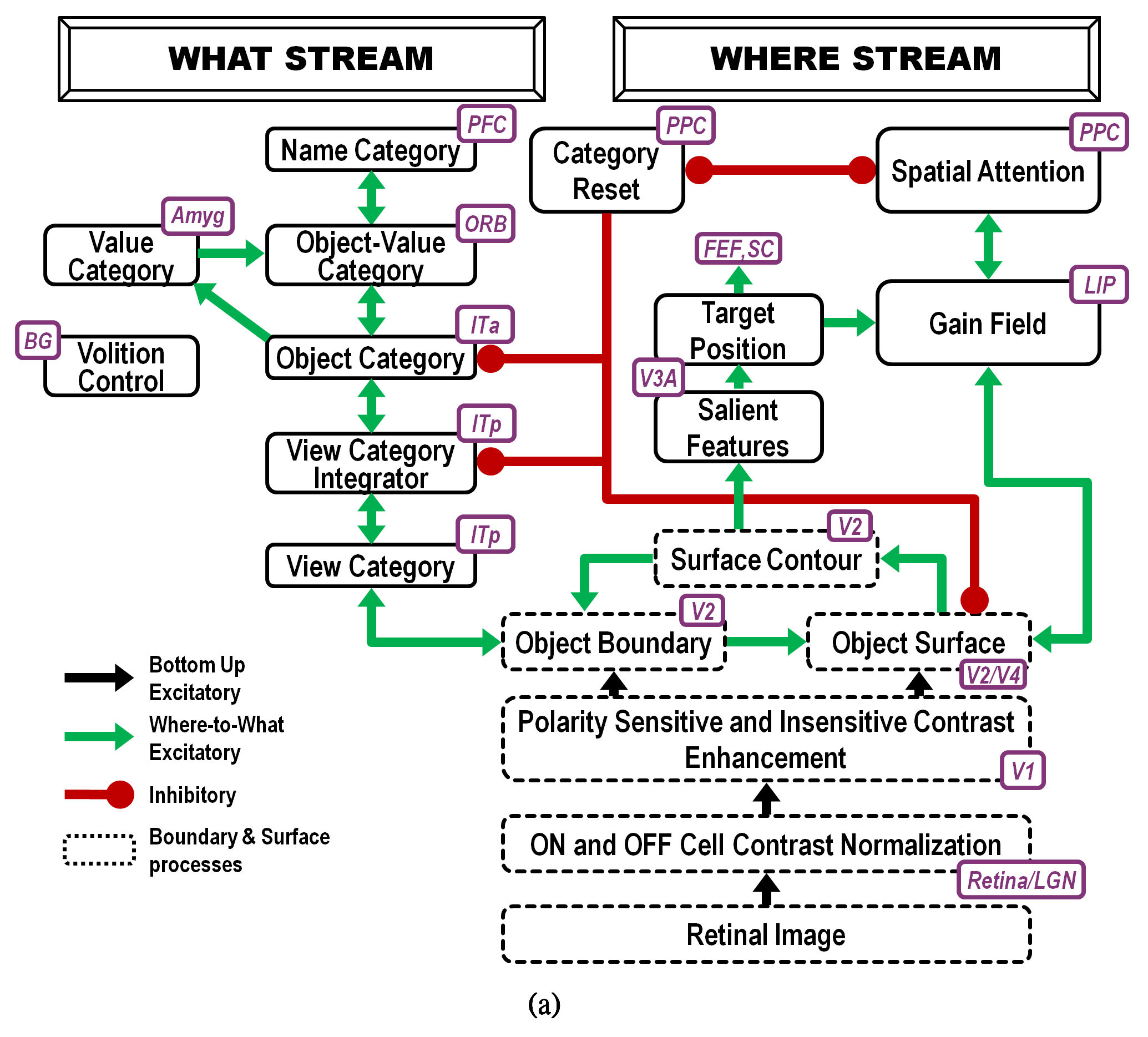 Fig. 18.
Fig. 18.Interactions of modelled brain regions within the ARTSCAN Search model enable them to learn to recognize and name invariant object categories. Invariant object category learning is modulated by Where-to-What stream interactions from spatial attention in the Where cortical stream-that is sustained by a surface-shroud resonance-and object attention in the What cortical stream-that obeys the ART Matching Rule. Dashed boxes indicate boundary and surface processes. Green arrows carry excitatory cortical signals from the Where stream to the What stream whereby invariant category learning and reinforcement learning occur. Red connections ending in circular disks indicate inhibitory connections. ITa: anterior inferotemporal cortex; ITp: posterior inferotemporal cortex; PPC: posterior parietal cortex; LIP: lateral intraparietal cortex; LGN: lateral geniculate nucleus; ORB: orbitofrontal cortex; Amyg: amygdala; BG: basal ganglia; PFC: prefrontal cortex; FEF: frontal eye fields; SC: superior colliculus; V1 and V2: primary and secondary visual areas; V3 and V4: visual areas 3 and 4. [Reprinted with permission from [5] published in Frontiers.]
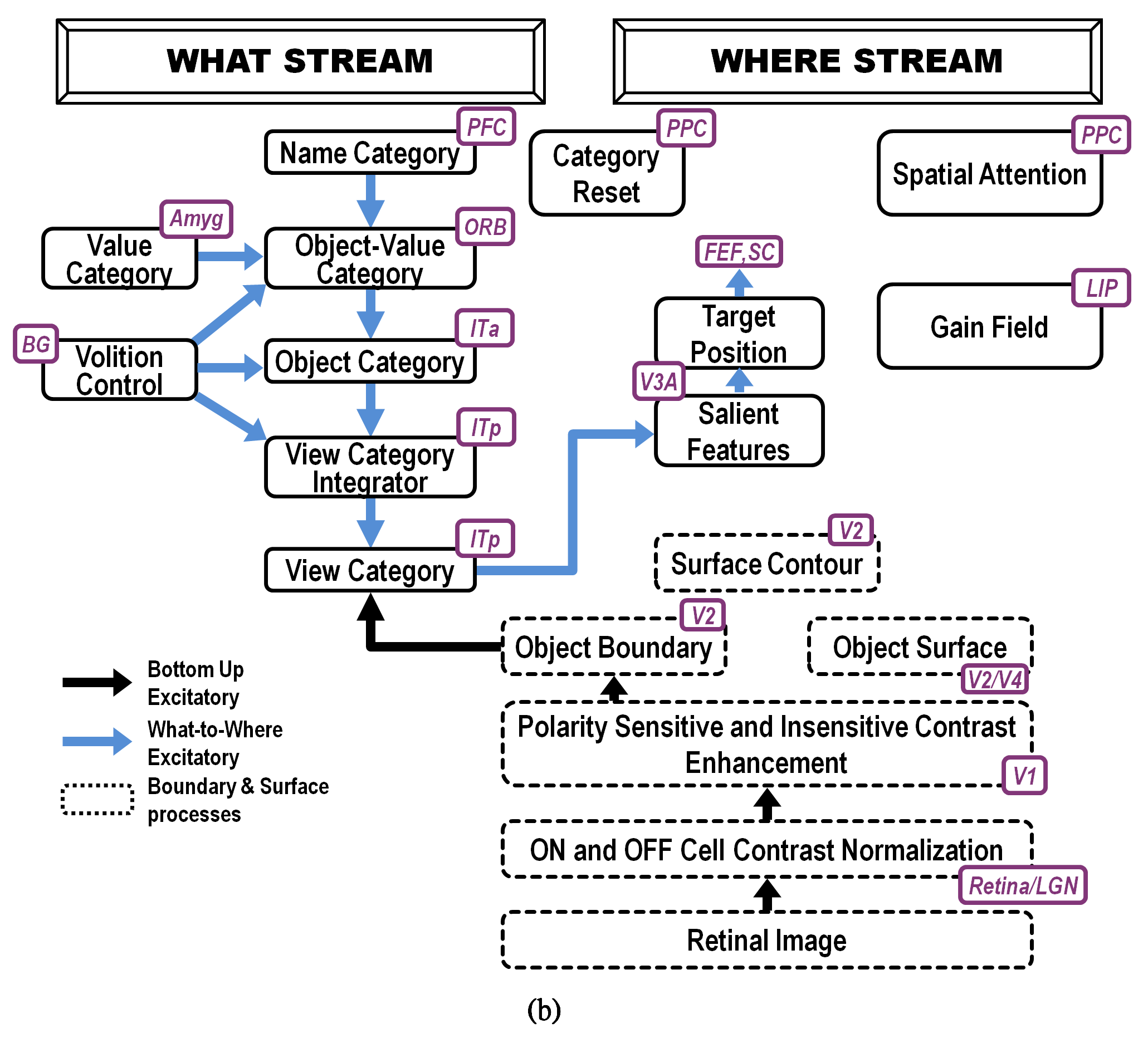 Fig. 19.
Fig. 19.ARTSCAN Search macrocircuit for Where’s Waldo search. A cognitive search for a desired object can be initiated by an object’s Name Category in the prefrontal cortex, or PFC. Search for a desired object can also be initiated by a Value Category in the amygdala, or Amyg. Either search can proceed via What-to-Where stream interactions. Black arrows represent bottom-up excitatory input signals. Blue arrows represent top-down excitatory search signals. Abbreviations are the same as in the caption of Figure 18. [Reprinted with permission from [5] published in Frontiers.]
The experiments of Brown and Denny [176] built upon experiments of Egly, Driver, and Rafal [177] who also studied how visual attention shifts between objects and locations, in both normal individuals and individuals with parietal lesions. Fig. 20 summarizes reaction time, or RT, data, as well as model computer simulations, from four different experimental conditions. These conditions are: (a) no shift of attention, (a) shift of attention to a different location on the same object, (c) shift of attention to a different location outside the object, and (d) shift of attention to a different location on a different object. In each condition, a cue precedes a target. Sometimes both are in the same object, sometimes in different objects, sometimes one outside an object, sometimes both outside an object.
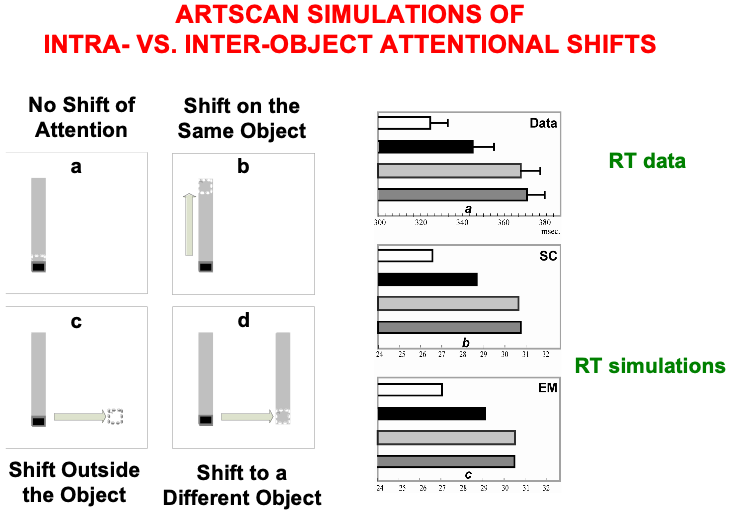 Fig. 20.
Fig. 20.Data from [176] about intra- vs. inter-object attentional shifts, and computer simulations of it by the ARTSCAN model [7]. [Adapted with permission from [7] published in Elsevier.]
Brown and Denney [176] showed that inter-object (Fig. 20d, left) and
object-to-location (Fig. 20c, left) shifts of attention take longer than
intra-object shifts (Fig. 20b, left). In all these cases, attention first needs
to be engaged at the location of the cue. They also found that shifting attention
from one object to another object, or from an object to another location, takes
nearly the same amount of time (369
In every condition, the cue and target trigger a surface attention signal to their location, thereby leading to the formation of a surface-shroud resonance. The longer reaction times in the inter-object and object-to-location attention shifts compared to intra-object attention shifts are simulated in ARTSCAN by the time it takes for an attentional shroud caused by the cue to collapse, and with it the corresponding surface-shroud resonance, before any other location or object can form a new shroud in response to the target. Reaction time, or RT, in each trial was computed in the model as the time it takes for surface contour or eye movement activity at the target location to reach a prescribed threshold.
The shroud does not collapse in the intra-object case. Instead, presenting a cue at one end of an object can cause a spread of both surface and boundary attention to the other end of the object. Such a spread of attention has been reported psychophysically by Roelfsema, Lamme, and Spekreijse [178] and simulated by Grossberg and Raizada [179]. Subsequent activation of surface attention by the target at the other end of the same object can add to the baseline of spreading attention, thereby reaching the RT threshold sooner than it can when the target lands outside the object.
The original ARTSCAN model could simulate only four of the nine experimental conditions that were reported by Brown and Denny [176]. Simulating the entire data set became possible in a consistent extension of ARTSCAN called distributed ARTSCAN, or dARTSCAN (Table 6). dARTSCAN is one of several ARTSCAN developments over the years aimed at explaining ever larger databases about invariant category learning and search (Fig. 21).
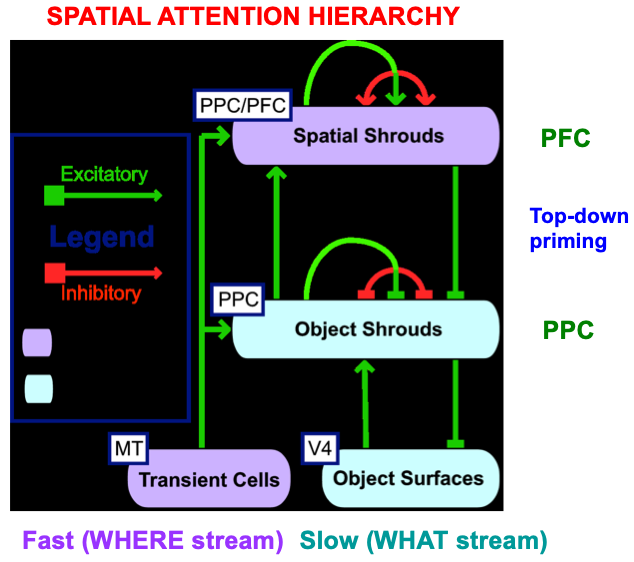 Fig. 21.
Fig. 21.The distributed ARTSCAN, or dARTSCAN, model adds spatial shrouds in the prefrontal cortex, or PFC, and both transient cell inputs from MT and sustained cell inputs from V4 to help form object shrouds and spatial shrouds in PFC and the posterior parietal cortex, or PPC. [Adapted with permission from [180] published in Elsevier.]

|
| Note: Fazl, Grossberg, and Mingolla [7]. Cao, Grossberg, and Markowitz [70]. Foley, Grossberg, and Mingolla [180]. Chang, Grosserg, and Cao [5]. Grossberg, Srinivasan, and Yazdanbakhsh [35]. |
The model circuits in Fig. 18 support learning of invariant object categories in the following way: Surface attention upon an object is maintained by a surface-shroud resonance between V2/V4 and PPC during learning of its view-invariant category. The attentional shroud in PPC that is maintained by the surface-shroud resonance inhibits a Category Reset stage that is also in PPC. Inhibition of Category Reset removes inhibition from ITa. The emerging view-invariant category in ITa can thus get associated with all the view-specific categories of the object that are learned in ITp. In this way, only views of the attended object can be incorporated into the view-invariant object category, thereby solving the view-to-object binding problem.
The model automatically controls surface attention shifts across the object so that it can inspect multiple object views to learn. These attention shifts use interactions between model cortical areas V2, V3A, V4, and LIP, among other brain regions. Details of these interactions, and data that support each of them, are found in [7].
When surface attention shifts to another object, the previously active surface-shroud resonance collapses, along with further category learning of the previously attended object. ARTSCAN can only learn view-invariant categories (Fig. 18). A consistent extension of ARTSCAN to the positional ARTSCAN, or pARTSCAN, model of Cao, Grossberg, and Markowitz [70] can learn view-, position-, and size-invariant object categories. pARTSCAN can, in turn, be extended to dARTSCAN in order to solve the Where’s Waldo problem after invariant category learning ends.
dARTSCAN further developed ARTSCAN to incorporate prefrontal spatial shrouds and transient signals from the Where stream to both PPC and PFC (Fig. 21). These processes, and more (e.g., affective processing regions like amygdala, or Amyg, and volitional control regions like basal ganglia, or BG), are included in the ARTSCAN Search architecture of Figs. 18 and 19. Within both dARTSCAN and the more general ARTSCAN Search architecture, all nine conditions of the Brown and Denny [176] experiments can be simulated (Fig. 22), not just the four that ARTSCAN could simulate (marked by *), in addition to data from many other experiments. Details of these explanations are provided in [5].
ART is a cognitive and neural theory of how our brains learn to attend, recognize, and predict objects and events in a changing world that may be filled with unexpected events. ART has the broadest explanatory and predictive range of current cognitive and neural theories. Its predictive power derives from its ability, shared with humans, to autonomously carry out fast, incremental, unsupervised and supervised learning and self-stabilizing memory in response to a changing world. ART hereby clarifies how humans can rapidly learn huge amounts of new information throughout life, and to integrate it into unified conscious experiences that support an emerging sense of self.
Fast learning in ART includes the possibility of learning an entire database on one learning trial [71, 73]. Our capacity for fast learning is often taken for granted, as when we see an exciting movie just once and then describe many details about it later to friends and family. In the laboratory, humans have been able to recognize thousands of pictures that they saw just once (e.g., [181, 182, 183, 184, 185, 186, 187, 188]). Indeed, the ARTSCENE neural model [25] shows how ART can rapidly learn to classify natural scene photographs, and outperforms alternative models in the literature which use biologically implausible computations. The combination of fast learning and stable memory, upon which all human civilization builds, is an evolutionary achievement that many other popular learning algorithms, such as back propagation and Deep Learning, do not have [42].
ART mechanistically explains how humans can rapidly learn about wide range of novel and changing environments, even with no prior instruction about the statistics of these environments. ART also explains how humans can rapidly learn these things without just as rapidly forgetting them. Neither we, nor ART models, ever need to worry that, by learning to recognize a new friend’s face within a few seconds, we will suddenly forget familiar faces of our family and friends. ART hereby avoids catastrophic forgetting. Most alternative neural learning algorithms, including back propagation and Deep Learning, do experience catastrophic forgetting [189, 190, 191], whether they try fast learning, or slow learning of an environment whose statistics change through time.
Grossberg [12] has called the problem whereby our brains learn quickly without catastrophically forgetting its past knowledge the stability-plasticity dilemma. The stability-plasticity dilemma must be solved by every brain system that hopes to adaptively respond to the “blooming buzzing confusion” of signals that we experience each day. ART solves the stability-plasticity dilemma by specifying mechanistic links between processes of between CLEAR processes. Grossberg [11, 12, 192] predicted that all brain processes that solve the stability-plasticity dilemma use CLEARS mechanisms.
ART uses CLEARS interactions to mechanistically explain why humans are intentional beings who pay attention to salient objects, why “all conscious states are resonant states”, and how we learn both many-to-one maps (representations whereby many object views, positions, and sizes all activate the same invariant object category) and one-to-many maps (representations that enable us to expertly know many things about individual objects and events). Fig. 23 summarizes what these concepts mean. How ART learns both kinds of maps will be explained after some more background is provided.
 Fig. 23.
Fig. 23.A supervised ARTMAP system can learn both many-to-one maps and one-to-many maps. [Reprinted with permission from [1] published in Oxford University Press.]
Before further explaining ART mechanisms, it is worth emphasizing that all of the foundational mechanisms of ART have received increasing support from subsequent psychological and neurobiological data since ART was introduced in [9, 10]. Since then, ART has undergone continual development to explain and predict increasingly large behavioral and neurobiological data bases, ranging from data about normal and abnormal human and animal perception and cognition, to the spiking and oscillatory dynamics of laminar thalamocortical networks in the visual and auditory modalities. Some of these ART models unify explanations and predictions about behavioral, anatomical, neurophysiological, biophysical, and even biochemical data. ART currently provides (e.g., [17]) functional and mechanistic explanations of such diverse topics as:
• laminar cortical circuitry;
• invariant object and scenic gist learning and recognition;
• prototype, surface, and boundary attention;
• gamma and beta oscillations;
• learning of entorhinal grid cells and hippocampal place cells;
• computation of homologous spatial and temporal mechanisms in the entorhinal-hippocampal system;
• breakdowns of vigilance control during autism and medial temporal amnesia;
• cognitive-emotional interactions that focus motivated attention on valued objects in an adaptively timed way;
• planning and control of sequences of linguistic, spatial, and motor events using item-order-rank working memories and learned list chunks;
• influence of subsequent speech sounds on conscious speech percepts of previous sounds;
• segregation of multiple noisy sources by auditory streaming; and
• normalization of speech sounds to enable learning and imitation of speech from speakers of all ages.
The brain regions that ART models to explain such processes include visual and auditory neocortex; specific and nonspecific thalamic nuclei; inferotemporal, parietal, prefrontal, entorhinal, hippocampal, parahippocampal, perirhinal, and motor cortices; frontal and supplementary eye fields; cerebellum; amygdala; basal ganglia; and superior colliculus.
As summarized in Table 4, our brains use different predictive mechanisms for perceptual/cognitive and spatial/motor learning that are carried out by computationally complementary cortical processing streams. Perceptual/cognitive processes in the What ventral cortical processing stream often use excitatory matching and match-based learning to create representations of objects and events in the world. Match-based learning in ART depends upon top-down learned expectations that focus prototype attention to solve the stability-plasticity dilemma. As noted above, this kind of learning can occur quickly without causing catastrophic forgetting. However, as Table 4 shows, match learning, and by extension ART, does not describe the only kind of learning that the brain needs to accomplish autonomous adaptation to a changing world. ART is thus not a “theory of everything”.
Excitatory matching and attentional focusing on bottom-up data using top-down expectations generates resonant brain states: When there is a good enough match between bottom-up and top-down signal patterns between two or more levels of processing, their positive feedback signals amplify, synchronize, and prolong their mutual activation (Fig. 5), leading to a resonant state that focuses attention on a subset of features (the category prototype, or critical feature pattern) that can correctly classify the input pattern at the next processing level and lead to successful predictions and actions. Amplification, synchronization, and prolongation of activity triggers learning in the more slowly varying adaptive weights that control the signal flow along pathways between the attended features and the recognition category with which they resonate. Such a resonance embodies a global context-sensitive indicator that the system is processing data worthy of learning, hence the name Adaptive Resonance Theory.
ART hereby models a link between the mechanisms which enable us to learn quickly and stably about a changing world, and the mechanisms that enable us to learn expectations about such a world, test hypotheses about it, and focus attention upon information that may predict desired consequences. ART hereby explains how, in order to solve the stability-plasticity dilemma, only resonant states can drive fast new learning.
Carpenter and Grossberg [71] mathematically proved that the simplest attentional circuit that solves the stability-plasticity dilemma is a top-down, modulatory on-center, off-surround network (Fig. 24). This ART Matching Rule provides excitatory priming of critical features in the on-center, and driving inhibition of irrelevant features in the off-surround. The modulatory on-center emerges from a balance between top-down excitation and inhibition, driven by neurons that obey the membrane equations of neurophysiology.
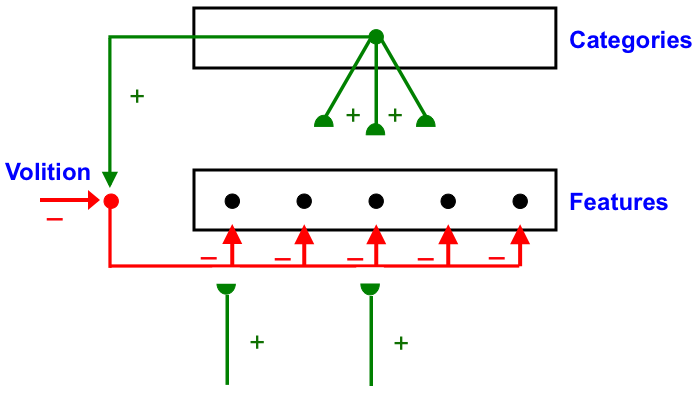 Fig. 24.
Fig. 24.The ART Matching Rule focuses prototype attention upon critical features that regulate category learning and prediction. It is realized by a top-down, modulatory on-center, off-surround network that also suppresses irrelevant features. See the text for details. [Adapted with permission from [193]. A closely related circuit appears in [71] published in Frontiers.]
Attentional priming by the modulatory on-center can be illustrated by the following example: Suppose you are asked to “find the yellow ball as quickly as possible, and you will win a $100,000 prize”. Activating a top-down, modulatory expectation of a “yellow ball” can subliminally enhance, or “prime”, the activity of its critical feature pattern, without causing these cells to generate suprathreshold activities. If and when the ball does appear, the primed cells can fire more energetically and rapidly. Sensory and cognitive top-down expectations hereby support excitatory matching with consistent bottom-up data (Table 4). In contrast, a big enough mismatch between a top-down expectation and bottom-up data can suppress the mismatched part of the bottom-up data, while attention focuses upon the matched, or expected, part of the bottom-up data.
Many anatomical and neurophysiological experiments have provided support for the ART prediction of how attention works, including data about modulatory on-center, off-surround interactions; excitatory priming of features in the on-center; suppression of features in the off-surround; and gain amplification of matched data (e.g., [194, 195, 196, 197, 198, 199, 200, 201, 202, 203]). The ART Matching Rule is often called the “biased competition” model of attention by experimental neurophysiologists [204, 205]. The ART Matching Rule property that bottom-up sensory activity may be enhanced when matched by top-down expectations is consistent with neurophysiological data showing facilitation by attentional feedback [178, 200, 206].
The experiments of Sillito et al. ([200], pp. 479-482) on attentional feedback from cortical area V1 to the Lateral Geniculate Nucleus (LGN) provided particularly strong support for an early prediction that the ART Matching Rule should acts in this circuit [10]. Sillito et al. [200] wrote that “the cortico-thalamic input is only strong enough to exert an effect on those dLGN cells that are additionally polarized by their retinal input…the feedback circuit searches for correlations that support the ‘hypothesis’ represented by a particular pattern of cortical activity”. Moreover, the “cortically induced correlation of relay cell activity produces coherent firing in those groups of relay cells with receptive-field alignments appropriate to signal the particular orientation of the moving contour to the cortex…this increases the gain of the input for feature-linked events detected by the cortex”.
In other words, top-down priming, by itself, cannot fully activate LGN cells. Instead, it needs matched bottom-up retinal inputs to do so, and the LGN cells whose bottom-up signals support cortical activity get synchronized and amplified by this feedback.
Additional anatomical studies have shown that the V1-to-LGN pathway realizes a top-down on-center off-surround network [200, 207, 208]. This kind of circuit also occurs during auditory processing: Zhang et al. [209] reported that feedback from auditory cortex to the medial geniculate nucleus (MGN) and the inferior colliculus (IC) also has an on-center off-surround form. Temereanca and Simons [210] have produced evidence for a similar feedback architecture in the rodent barrel system.
The appearance of the ART Matching Rule circuit in multiple modalities can be understood from the need to solve the stability-plasticity dilemma during development and learning in all of them.
The ART
Matching Rule has been represented mathematically in a similar way by more than
one lab. In particular, the “normalization model of attention” [211] simulates
several types of experiments on attention using the same equation that the
distributed ARTEXture (dARTEX) model ([145], equation (A5)) used to simulate
human psychophysical data about Orientation-Based Texture Segmentation (OBTS) of
Ben-Shahar and Zucker [212]. Reynolds and Heeger [211] defined an
algebraic equation for attention with built-in divisive terms to model
normalization. Bhatt et al. [145] modeled attention using the dynamics of
an ART neural network model. When these dynamics reach steady state, the
resulting algebraic equation includes a divisive term that is not built
explicitly into ART dynamics. The divisive term arises from the automatic gain
control, or shunting, terms that occur in Eqn. 1. When such an equation reaches equilibrium,
its time derivative dx
A balance between excitation and inhibition in the on-center of a top-down expectation is what makes it modulatory. This balance can be modified by volitional gain control signals from the basal ganglia (Fig. 24). For example, if volitional signals inhibit inhibitory interneurons in the on-center, then read-out of a top-down expectation from a recognition category can fire, not merely modulate, cells in the on-center prototype. Such volitional control may control mental imagery and the ability to think and plan ahead before choosing an appropriate action.
A similar modulatory circuit, again modulated by the basal ganglia, is predicted to control temporary storage in the prefrontal cortex of sequences of events in working memory [31] and a task-appropriate span of spatial attention (“useful-field-of-view”) in the parietal and prefrontal cortex [180].
ART predicts that all these properties arise from a circuit design which uses top-down expectations to dynamically stabilize fast learning throughout life. This ability to learn quickly without catastrophic forgetting can then be volitionally modulated by the basal ganglia to support imagination, internal thought, and planning. This modulation has brought huge evolutionary advantages to human civilization.
When basal ganglia modulation breaks down, various clinical disorders can occur. In particular, if these volitional signals become tonically hyperactive, then top-down expectations can fire without overt intention, leading to properties like schizophrenic hallucinations [213]. Such mental disorders have probably persisted because the evolutionary advantages of the circuits that allow them are so momentous.
Match learning occurs only if a good enough match occurs between bottom-up information and a learned top-down expectation that is read out by an active recognition category. A good enough match can trigger an adaptive resonance that learns a time-average of attended critical feature patterns. Such learning leads to stable memories of arbitrary events presented in any order.
Match learning, by itself, is insufficient for an obvious reason: If learning occurs only when a good enough match occurs between bottom-up data and learned top-down expectations, then how is anything really novel learned? ART solves this problem by using an interaction between complementary processes of resonance and reset that control attentive learning and memory search, respectively. These processes balance between processing the familiar and the unfamiliar, the expected and the unexpected. When an input is unexpected but familiar, memory search can discover a better matching, but known, category. When an input is unexpected and unfamiliar, search can discover an uncommitted cell population with which to learn a new category.
The resonance process is predicted to take place in an attentional system within the What cortical stream, in brain regions like the temporal and prefrontal cortices (Table 7). This system computes processes like resonance, prototype attention, learning and recognition. It is here that top-down expectations that obey the ART Matching Rule are matched against bottom-up inputs. When a top-down expectation achieves a good enough match with bottom-up data, this match process focuses prototype attention upon those critical features in the bottom-up input that are expected. If the expectation is close enough to the input pattern, then a state of resonance develops as the attentional focus takes hold, which is often realized by oscillatory dynamics that synchronize the firing properties of the resonant neurons [214].
|
A sufficiently bad mismatch between an active top-down expectation and a bottom-up input activates the complementary orienting system, which includes the hippocampal system and the nonspecific thalamus (Table 7). Output signals from the orienting system rapidly reset the recognition category that has been reading out the poorly matching top-down expectation (Fig. 25). The cause of the mismatch is hereby removed, thereby freeing the system to activate a different recognition category. To discover a better matching category, the reset event triggers memory search, or hypothesis testing.
Fig. 26
describes how the ART hypothesis testing and learning cycle works that is
triggered by a reset. In Fig. 26a, a bottom-up input feature pattern, or
vector, I (represented by the upward facing green arrow to the first
level F
 Fig. 26.
Fig. 26.The ART hypothesis testing and category learning cycle. [Adapted with permission from [193]. A closely related figure appears in [71] published in Elsevier.]
The active category cells, in turn, send top-down signals
U back to F
The first time that a recognition category is activated in F
With this caveat in mind, it follows that, on every learning trial, matching
between the input vector I and V selects that subset X* of F
If the top-down expectation matches the bottom-up input pattern well enough, then the pattern X* of attended features reactivates the category Y which, in turn, reactivates X*. The network hereby locks into a resonant state through a positive feedback loop that dynamically links, or binds, the attended features across X* with their category, or symbol, Y. A feature-category resonance (Table 1) results that synchronizes, gain amplifies, and prolongs the activities of the critical features and the category to which they are bound (Fig. 5), triggers learning of the critical features within both the bottom-up adaptive filter and the top-down learned expectation, and supports conscious recognition of the attended visual object or event.
Individual features at F
The next few sections describe the implications of the ART hypothesis testing and learning cycle in greater detail to clarify several basic issues about how ART benefits from Complementary Computing.
The attentional and orienting systems in an ART network play complementary roles during category learning and search for new categories. I will explain below that these complementary roles derive from computationally complementary laws that are obeyed by the ART attentional and orienting systems, in addition to the complementary laws that are summarized in Table 3, and the four of these that have already been discussed above.
The reason for this complementary relationship is as follows: When there is a good enough match in the attentional system, the bound state between critical features and their active category embodies information about the features that are currently being processed. However, at the moment when a predictive error occurs, the network does not know why the currently active category has failed to predict the correct outcome. Furthermore, when such a predictive mismatch in the attentional system activates the orienting system, the orienting system has no knowledge about what went wrong in the attentional system, just that something went wrong.
Thus, the attentional system has information about how inputs are categorized, but not whether the categorization is correct, whereas the orienting system has information about whether the categorization is correct, but not about what is being categorized. Given that neither system knows at the time of mismatch what went wrong, how does an ART memory search discover a more predictive outcome?
Because the orienting system does not know what category in the attentional system caused the predictive error, its activation needs to equally influence all cells in the category level. That is why a big enough mismatch in the orienting system triggers a burst of nonspecific arousal that equally activates all cells in the attentional system. In other words: Novel events are arousing! As shown in Fig. 26c, such an arousal burst selectively resets category cells that caused the mismatch, thereby initiating memory search, or hypothesis testing, to discover a more predictive category (Fig. 26d). Such a memory search shifts prototype attention from one category to another.
How does a burst of nonspecific arousal selectively reset active category cells? Why do not the winning category cells remain winners after arousal acts?
Arousal-mediated category reset is selective because signals within the category level are multiplied, or gated, by habituative chemical transmitters, or MTM traces (see Eqn. 2). Due to habituative gating, recently activate category cells are more habituated than inactive cells. The habituated category cells compete with other cells at the category level to determine which cells will be chosen next. This is a self-normalizing competition that is carried out by recurrent shunting on-center off-surround interactions across the category level (see Eqn. 1). Self-normalization interacts with habituation to suppress the habituated category cells, even though they were the most active cells when the arousal burst is received. This self-normalization property is also a computational basis of the limited capacity of attention (e.g., [87, 215, 216, 217]).
Mathematical proofs of how reset, or antagonistic rebound, happens can be found in [12] (Appendices A and E) and [14] (Appendix). Once the maximally activated cells are suppressed by a combination of habituation and competition during the search cycle, cells that initially got smaller inputs than the original winning cells can inherit the self-normalizing network activity that the winning cells no longer take up, and thereby become more active in the next time interval. This cycle of mismatch-arousal-reset continues until resonance can again occur.
Because the total activity of the category cell network is self-normalizing, the category level activations can be interpreted as a kind of “real-time probability distribution”, and the ART memory search cycle can be interpreted as a kind of probabilistic hypothesis testing and decision making that is competent in response to arbitrarily complicated non-stationary time series of input patterns. These properties are what makes ART a self-organizing production system in a changing world [42].
Psychological and neurobiological data have supported ART predictions about how the memory search process works. A particularly compelling kind of data have been derived from experiments using event-related potentials, or ERPs, that are measured from a human subject using arrays of scalp potentials.
For example, the predicted sequence of mismatch, arousal, and category reset operations during an ART search have been experimentally predicted, recorded, and modeled by Banquet and Grossberg [3] as sequences of P120, N200, and P300 ERPs during oddball experiments. During such an experiment, a human subject is primed to detect rare targets within sequences of more frequent distractors (Fig. 27).
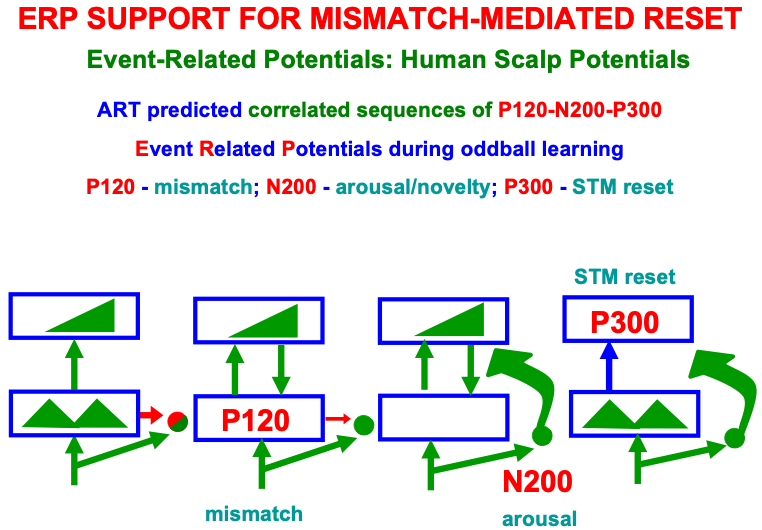 Fig. 27.
Fig. 27.Event Related Potential, or ERP, experimental support for the ART hypothesis testing cycle from [3]. [Reprinted with permission from [1] published in Oxford University Press.]
In addition to ERP events that occur during search, the Processing Negativity, or PN, ERP has been recorded during sustained prototype attention [218, 219] while an ART feature-category resonance occurs.
The N200 ERP that is triggered by mismatch-mediated activation of the orienting system [220, 221, 222] has properties that are computationally complementary to those of PN, as summarized in Fig. 28. The complementary properties of PN (within the attentional system) and N200 (within the orienting system) make precise the sense in which the ART attentional and orienting systems are computationally complementary.
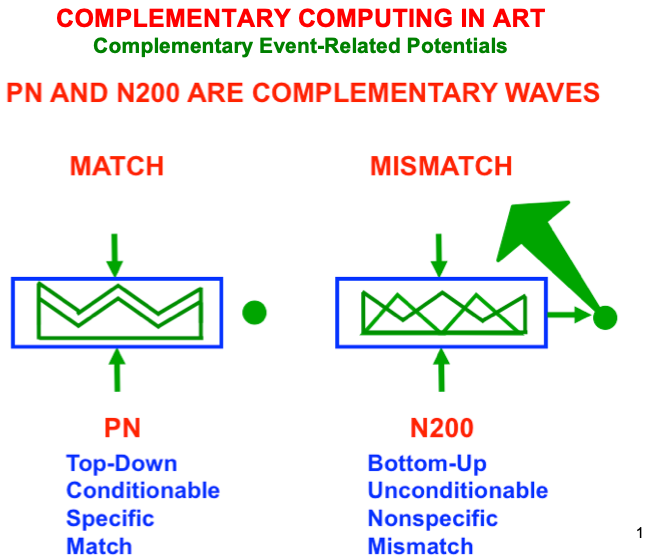 Fig. 28.
Fig. 28.The processing negativity (PN) and N200 ERPs illustrate the fact that the ART attentional and orienting systems are computationally complementary. [Adapted with permission from [19] published in Elsevier.]
ERP data have been supplemented by neurophysiological data about attentional and orienting system interactions. For example, Brincat and Miller ([223], p. 576) have reported neurophysiological data from prefrontal cortex (PFC) and hippocampus (HPC) in monkeys learning object-pair associations: “PFC spiking activity reflected learning in parallel with behavioral performance, while HPC neurons reflected feedback about whether trial-and-error guesses were correct or incorrect. Rapid object associative learning may occur in PFC, while HPC may guide neocortical plasticity by signaling success or failure via oscillatory synchrony in different frequency bands”.
PFC is a projection area of the inferotemporal, or IT, cortex where categories begin to be learned. These data thus add to a substantial experimental literature that have implicated the hippocampus as part of the orienting system for match/mismatch processing. See [19] for additional discussion of this literature.
How specific and concrete, or general and abstract, will learned ART categories be? On what combination of critical features will categories learn to focus prototype attention?
This is determined by how good a match is needed in order for resonance,
attention, learning, and consciousness to occur. The matching criterion is
determined by the size of a vigilance parameter
The vigilance parameter
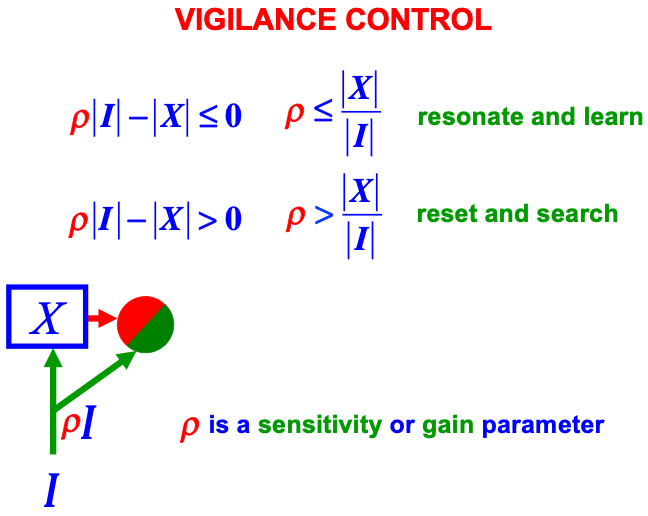 Fig. 29.
Fig. 29.How vigilance determines whether the attentional system will resonate and learn, or the orienting system will be activated to drive memory search and hypothesis testing. [Adapted with permission from [1] published in Oxford University Press.]
Vigilance is typically chosen as low as possible to learn the most general possible categories, and thereby conserve memory resources, but without causing a reduction in predictive success. The baseline vigilance level is therefore set initially at the lowest level that has led to predictive success in the past. When a given task requires finer discriminations, vigilance is raised.
Predictive successes and failures can be computed in an ARTMAP system that is capable of learning to predict any number of arbitrarily large output vectors in response to any number of arbitrarily large input vectors ([75, 77]). An ARTMAP system is composed of two unsupervised ART systems, ARTa and ARTb, that are linked by associative learning in a map field (Fig. 30). By pairing an input vector a with an output vector b, an ARTMAP system can learn to associate input vector a with output vector b, thereby becoming a supervised mapping system. Input vector a can learn to predict output vector b because of the reciprocal bottom-up and top-down learned connections in both ARTa and ARTb.
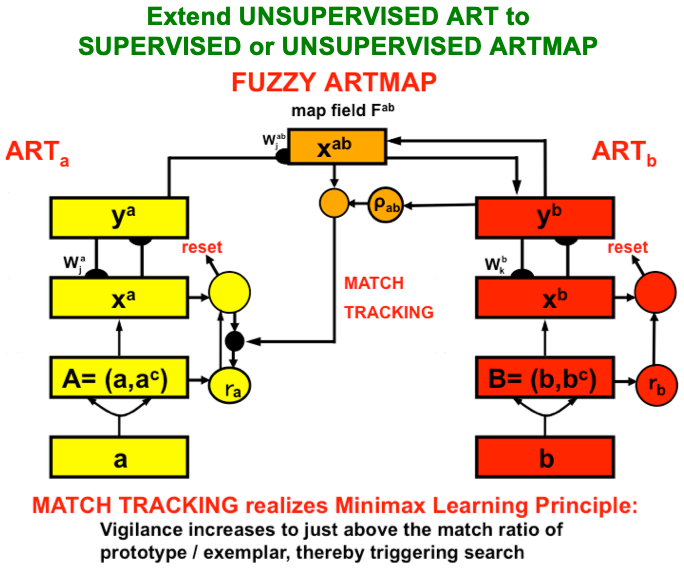 Fig. 30.
Fig. 30.ARTMAP systems can carry out arbitrary combinations of unsupervised or supervised learning during learning trials. During supervised learning, two unsupervised ART systems, ARTa and ARTb, are linked by a learned associative map which enables learning a map from arbitrarily large databases of m-dimensional vectors to n-dimensional vectors, where m and n can also be chosen arbitrarily large. [Adapted with permission from [75] published in Frontiers.]
ARTMAP clarifies how many-to-one maps and one-to-many maps are learned. Figs. 31 and 32 show one example of each. In the many-to-one example in Fig. 31, arbitrarily many, arbitrarily large vectors of medical symptoms, tests, and treatments can learn to predict multiple different medical outcomes of these combined constraints, including the estimated length of stay in the hospital. Fig. 32 illustrates how ARTMAP can learn a one-to-many map. For example, after learning to predict that the image on the bottom left is a dog, seeing that image leads to the response “dog”. However, if instead the answer “Rover” is given, then the mismatch between “dog” and “Rover” triggers an ART search in which prototype attention shifts to focus on that combination of features in the image that predicts the particular dog “Rover”.
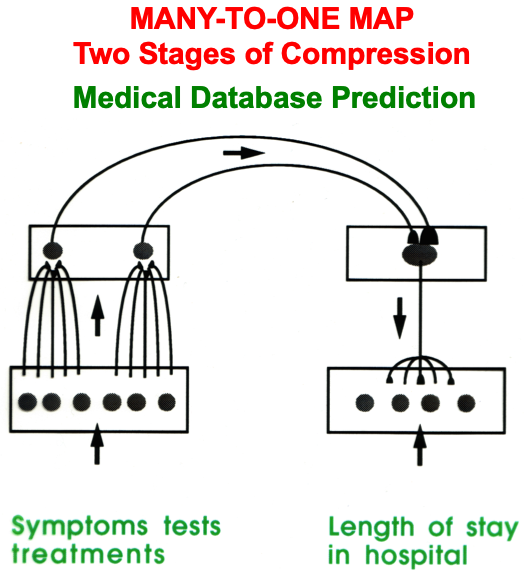 Fig. 31.
Fig. 31.ARTMAP systems can learn both many-to-one maps and one-to-many maps. Learning of a many-to-one map is illustrated in this figure. ARTa is trained to classify combinations of symptoms, tests, and treatments of medical disorders. ARTb is trained to classify properties of hospital care. Predictive errors in ARTb can drive memory searches in ARTa to focus attention upon, and learn to classify, predictive combinations of critical features about disease measurements with which to learn correct predictions about hospital care. [Reprinted with permission from [1] published in Oxford University Press.]
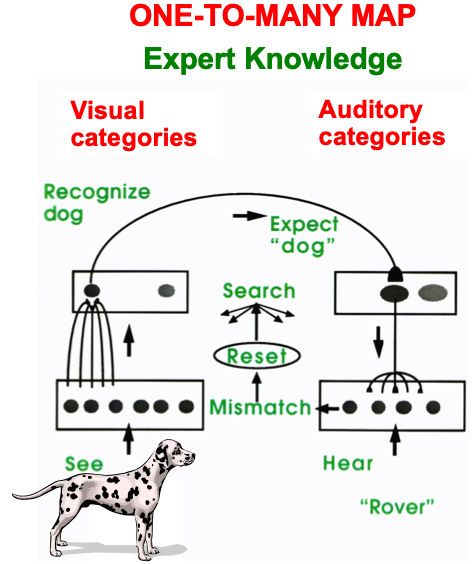 Fig. 32.
Fig. 32.An example of how a one-to-many map is learned by ARTMAP: After the association between the image and the name “dog” has been learned, showing the image on a subsequent trial with the teaching signal “Rover” causes a predictive mismatch between “dog” and “Rover” that drives a memory search which ends by focusing prototype attention upon a combination of critical features that is sufficient to recognize “Rover”. These critical features drive learning of a new category that is associated with the name “Rover”. An arbitrarily number of such associations can be learned in response to the image. These learned links can then be organized by higher categories that code all of this knowledge about the image. [Reprinted with permission from [1] published in Oxford University Press.]
Vigilance it typically raised in response to a
predictive failure, or disconfirmation, because it must have been lower than the
previously computed match value
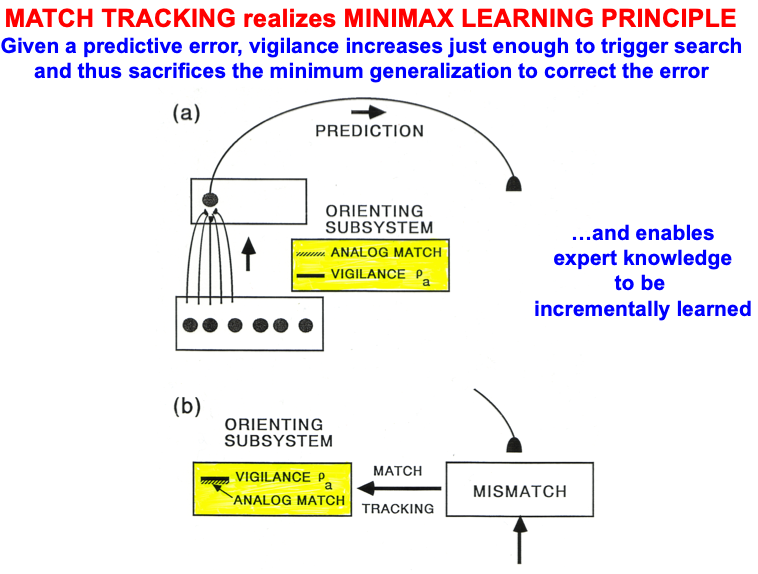 Fig. 33.
Fig. 33.Minimax learning by matching tracking minimizes predictive error while conjointly maximizing category generality. See the text for details. [Reprinted with permission from [42] published in Frontiers.]
Match tracking helps to explain how one-to-many maps are learned. It also helps to explain how predictive errors are corrected. For example, a predictive error could occur if a viewer classifies an object as a dog, whereas it is really a wolf. Within ART, such a predictive disconfirmation causes an increase in vigilance that triggers a memory search. The memory search causes a shift in prototype attention to focus on a different combination of features that can successfully be used to recognize a wolf, and perhaps to recognize other similar looking wolves as well.
The vigilance increase in Fig. 33b is called match tracking because
vigilance tracks the match
All the neurons in cerebral cortex are organized using a shared design of layered circuits whose specializations carry out all forms of higher-order biological intelligence [224, 225]. As noted in [192], this design realizes a revolutionary computational synthesis of the best properties of feedforward and feedback processing, digital and analog processing, and data-driven bottom-up processing and hypothesis-driven top-down processing. Top-down processing including the focusing of attention.
The understanding of ART, and attention, incrementally developed until Grossberg [226] introduced the LAMINART model to show how bottom-up adaptive filtering, horizontal grouping, and top-down attentional interactions may be combined in the laminar circuits of neocortex. This article introduced the computational paradigm of Laminar Computing, which shows how predicted ART mechanisms may be embodied within known laminar cortical circuits, and solves a long-standing open problem, called the attention-preattention interface problem, thereby enabling the explanation and prediction of much more cognitive and brain data than before. More about the attention-preattention interface problem will be described in the next section.
This laminar synthesis combined ART as a theory of category learning and prediction—which emphasized bottom-up and top-down interactions within higher cortical areas such as V4, inferotemporal cortex, and prefrontal cortex—with the FACADE (Form-And-Color-And-DEpth) theory of 3D vision and figure-ground perception—which emphasized bottom-up and horizontal interactions for sensory filtering, followed by completion of boundaries and filling-in of surface brightness and color, within lower cortical processing areas such as V1, V2, and V4.
The unification of these two research streams in LAMINART proposed how all cortical areas combine bottom-up, horizontal, and top-down interactions, thereby beginning to functionally clarify why all granular neocortex has a characteristic architecture with six main cell layers [175]. In particular, this unification led to laminar neural models within variations of a shared canonical cortical design could be used to explain psychological and neurobiological data about vision, speech, and cognition. See [17] for a review.
Fig. 34 shows the cortical circuit that realizes prototype attention within the visual cortex. Note that a top-down signal from layer 6 of a higher cortical area like V2 feeds topographically down to layer 6 of V1, either directly or via apical dendrites of layer 5 cells (as shown), before folding back up to layer 4 as a modulatory on-center, off-surround network. Prototype attention in visual cortex is thus realized by a folded feedback circuit.
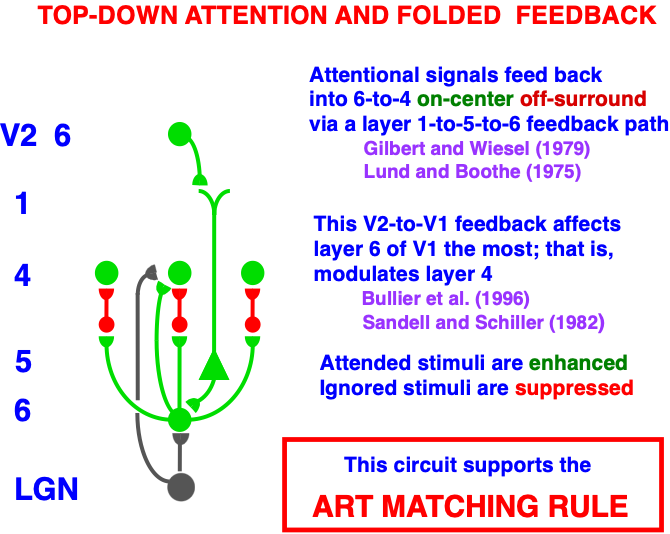 Fig. 34.
Fig. 34.Laminar circuit that carries prototype attention from layer 6 of cortical area V2 to layer 4 of cortical area V1 via a top-down, modulatory on-center, off-surround network that embodies the ART Matching Rule using a folded feedback circuit from layer 6 in V2 to layers 5-to-6-to-4 in V1. [Reprinted with permission from [1] published in Oxford University Press.]
Fig. 34 also shows that bottom-up filtering signals from the lateral geniculate nucleus, or LGN, to V1 and top-down attention from V2 to V1 share the modulatory on-center, off-surround decision circuit between layers 6 and 4. In this way, bottom-up input patterns can have critical features selected by top-down prototype attention in layer 4 of V1.
Fig. 35 shows that, in addition, long-range horizontal interactions in layer 2/3 (shown in black), which carry out boundary completion and perceptual grouping, also share the same decision circuit between layers 6 and 4. See, in particular, the excitatory pathway from layer 2/3 to layer 6.
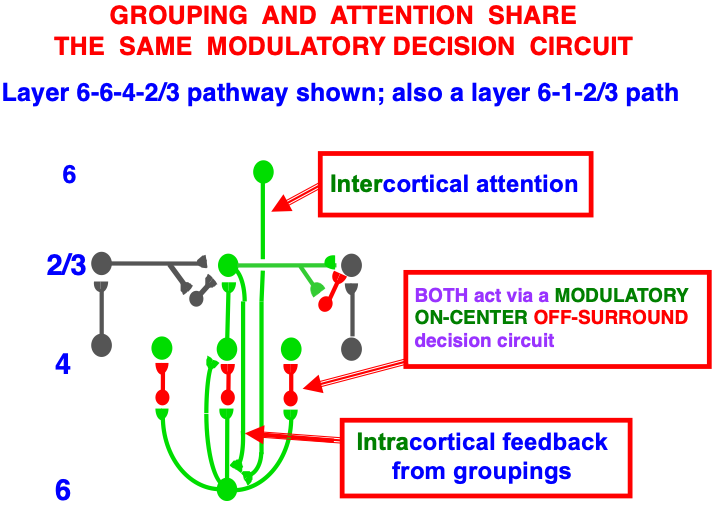 Fig. 35.
Fig. 35.Laminar circuit that joins the prototype attention circuit with a boundary completion circuit: Both boundary grouping and prototype attention share the same layer 6-to-4 decision circuit that uses modulatory on-center, off-surround interactions to choose the grouping that best balances between grouping and attentional constraints. The horizontal connections in layer 2/3 that complete boundary groupings use signals from layer 2/3-to-6-to-4, where they interaction with prototype attentional signals. [Reprinted with permission from [1] published in Oxford University Press.]
Thus all the constraints of bottom-up adaptive filtering, horizontal grouping, and top-down attentive expectations share the same decision circuit between layers 6 to 4, thereby multiplexing all of their constraints before the best attentional focus and perceptual grouping is chosen in the current informational context. I therefore call this circuit the attention-preattention interface.
The Synchronous Matching ART, or SMART, model [214] extends the LAMINART model
to include hierarchies of laminar neocortical circuits that use spiking neurons
to interact within and between each other, and with specific and nonspecific
thalamic nuclei (Fig. 36). SMART explains and predicts the functional meaning
of a larger body of anatomical data, of synchronized cortical interactions, and
of the biochemical substrates of vigilance control. One anatomical refinement in
Fig. 36 models different roles for cortical layers 6
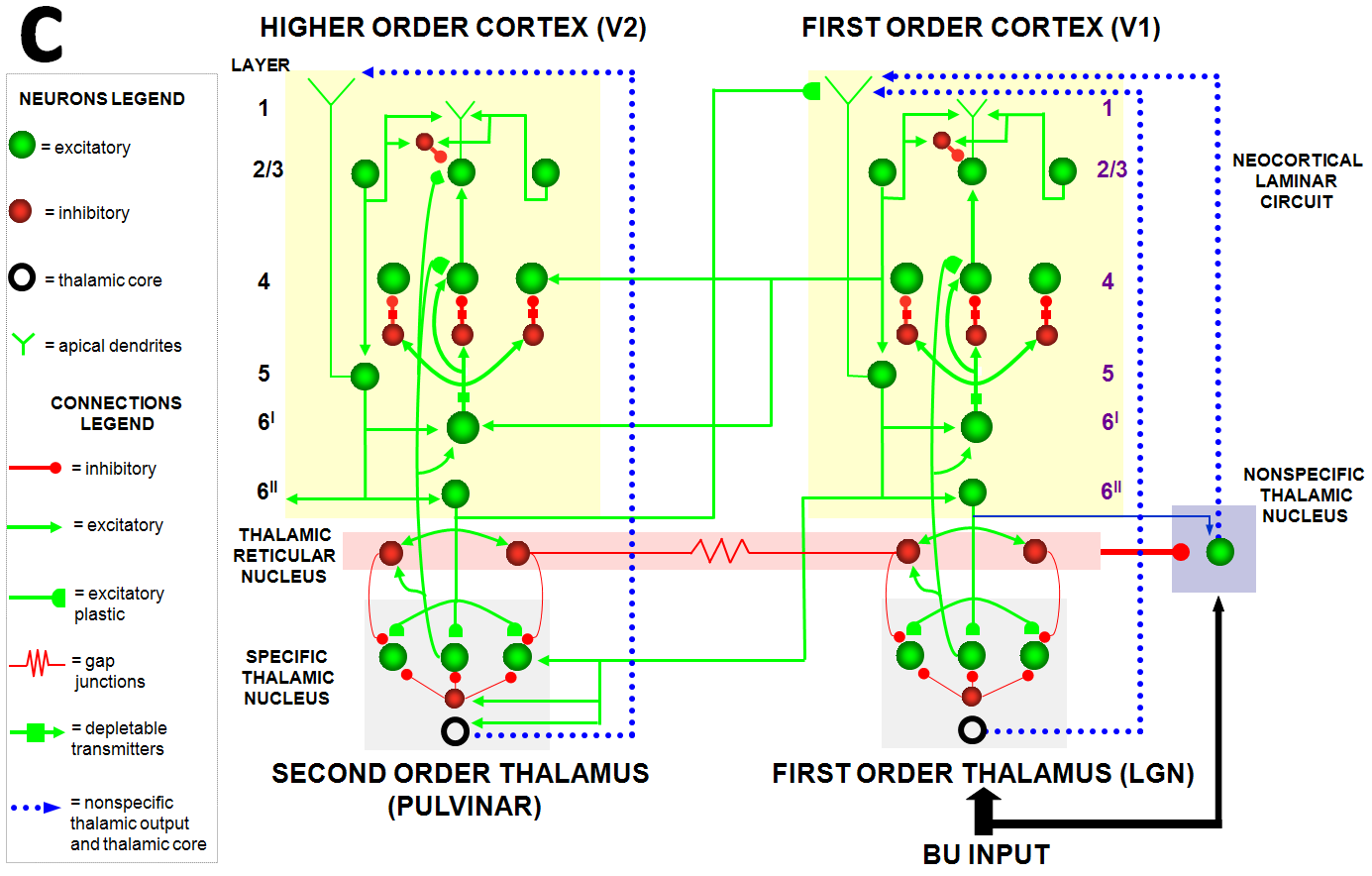 Fig. 36.
Fig. 36.Synchronous Matching ART, or SMART, microcircuit showing a hierarchy of laminar cortical areas interacting with both specific and nonspecific thalamic nuclei in order to incrementally learn a hierarchy of recognition categories. [Adapted with permission from [214] published in Elsevier.]
SMART simulations of synchronized cortical oscillations show how a good enough top-down attentive match may lead to fast gamma oscillations that support prototype attention and spike-timing dependent plasticity (STDP). In contrast, a big enough mismatch may generate slower beta oscillations. This match-mismatch gamma-beta story seems to occur in quite a few brain systems, with data supporting this prediction having recently been reported in V1, frontal eye fields, and hippocampus, as reviewed in [17].
Of particular interest is the SMART prediction about how vigilance is controlled in our brains. As shown in Fig. 37, a big enough mismatch in the nonspecific thalamus activates the nucleus basalis of Meynert [120], which, in turn, broadly releases acetylcholine, or ACh, in layer 5 of multiple cortical areas. ACh release reduces after-hyperpolarization (AHP) currents, which cause a transient increase in vigilance. If this increase is large enough (see Fig. 29), then it can disrupt an ongoing resonance to trigger a memory search, ending in selection or learning of a category with a new focus of prototype attention. Many data about the role of ACh in vigilance control and reset are summarized and modeled in [227].
 Fig. 37.
Fig. 37.Circuit showing how a big enough mismatch activates the nonspecific thalamus, which activates the nucleus basalis of Meynert, which releases acetylcholine, or ACh, in layer 5 of multiple cortical areas. The ACh reduces afterhyperpolarization, or AHP, currents and thereby causes an increase in vigilance. [Adapted with permission from [214] published in Elsevier.]
In normal individuals, this vigilance circuit controls processes like match tracking. In various mental disorders-such as Alzheimer’s disease, autism, amnesia, and disordered sleep-the circuit can break down in different ways, leading to behavioral symptoms of each disorder. Grossberg [18] describes what these symptoms are and how they may arise due to ACh malfunctions.
After spatial attention orients to the position of a desired goal object, movements must follow to acquire it. One of the most important kinds of movements are saccadic, or ballistic, eye movements to foveate the target, followed by leg movements to navigate towards it, and arm movements to reach it.
The superior colliculus, or SC, contains a map of possible target positions. It is a multimodal map in which visual, auditory, and planned movement inputs compete for attention, leading to selection of a winning position that controls where the next saccadic eye movement will go. Visual and auditory signals are computed in different coordinates: Visual targets are registered on the retina, so are initially computed in retinotopic coordinates. The position in space that this retinal activation represents depends upon where the eyes are looking when they receive this retinal input. Both the position on the retina of the target, and the position of the eyes in their orbit, thus combine to compute target position. Auditory signals are computed in head-centered coordinates, since the ears move with the head.
Learning within the deeper layers of the SC converts these different coordinates into a shared coordinate system using visual inputs as a teaching signal. That is why both auditory and planned inputs get converted into a retinotopic coordinate system, that also codes a motor error map because each of its positions codes the direction and distance that a saccade must move in order to foveate a target a target at that position (Fig. 38). This learning process ensures that auditory, visual, and prefrontal planning inputs that represent the same position in space activate the same SC map position with which to select the target position of the next saccade. Multiple auditory, visual, and cognitive inputs to the SC compete through time to determine this winning target position. As in the case of cognitive category attention, learning, and choice, this competition is realized by a recurrent on-center off-surround network.
 Fig. 38.
Fig. 38.(a) Retinal activation by a visual signal generates a reactive visual target signal to the peak decay, or burst, layer of the superior colliculus, or SC. This signal topographically activates the spreading wave, or buildup, layer of the SC. Other things being equal, the buildup cells activate the saccade generator, or SG, in the peripontine reticular formation to generate a saccadic eye movement. This movement is calibrated by learned adaptive gain control signals from the cerebellum, or adaptive gain (AG) stage. (b) When the SG fires, it generates both a signal to move the eye and a parallel corollary discharge signal that codes the current eye position in motor coordinates. The corollary discharge signal is added to the retinotopically-coded position of the target to define a head-centered spatial map of the target. (c) The head-centered representation of target position is converted into an error vector that is coded in motor coordinates when a corollary discharge of the current eye position, also coded in motor coordinates, is subtracted from it. This motor error vector codes the direction and distance that the eye needs to move to foveate the target. The hemi-disk denotes an adaptive synapse where head-centered and motor coordinates are rendered dimensionally consistent. This learning occurs when the eye is steadily looking at stationary target positions, so that the desired and current eye positions are the same. The motor error vector that is calibrated in this way is then converted into a motor error map. (d) The motor error map learns to activate the SC position of the target using inputs from the peak decay layer as teaching signals. The learned transformation from reactive target position to commanded SC saccadic eye movement is then complete. [Reprinted with permission from [228] published in Wiley.]
The SACCART model [228] models multimodal map learning and choice within the deeper layers of the SC. Model interactions quantitatively simulate the temporal dynamics of SC burst and buildup cells under a variety of experimental conditions (Fig. 39). Burst cells respond with bursts that decay as the next saccadic position is chosen and performed. Buildup cells generate a spatially distributed pattern of activity that begins at the chosen position and then spreads towards the fovea as they command the eye to foveate.
 Fig. 39.
Fig. 39.Comparison of model processes with anatomical and neurophysiological correlates. (a) Schematic representation of model interactions. (b) Data correlates of the model depicted in (a). SNr: substantia nigra pars reticulata; PPRF: peripontine reticular formation; MRF: mesencephalic reticular formation; peak decay cells: burst, or T, cells; spreading wave cells: buildup, or X, cells. [Reprinted with permission from [228] published in Wiley.]
This SC model is called SACCART because it is a specialized ART circuit whose map learning may be viewed as a kind of attentive motor category learning that takes place using bottom-up and top-down interactions between burst and buildup cells (Fig. 40). These ART dynamics also allow resonance to occur between burst and buildup cells when they choose the same target position (Fig. 40a), and reset within burst cells when a planned and reactive cue represent different possible saccadic targets (Fig. 40b).
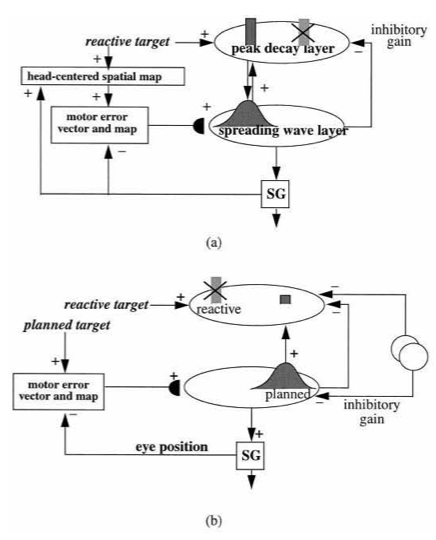 Fig. 40.
Fig. 40.(a) Topographically organized excitatory feedback between the spreading wave and peak decay layers triggers a resonance that drives the SC map learning process. A nonspecific inhibitory gain signal from the spreading wave layer reaches all target positions in the peak decay layer via the mesencephalic reticular formation [229, 230, 231]. Together these excitatory and inhibitory interactions embody the ART Matching Rule, thereby supporting the SACCART model name. An attended target position is chosen by competitive interactions within these layers, while also suppressing positions of irrelevant targets, thereby stabilizing map learning by preventing irrelevant targets from being learned. (b) Auditory, planned, and visual targets compete for attention in the deeper layers of the SC [232, 233]. Auditory or planned targets are received in the SC deeper layers, whereas reactive target signals are received by the superficial layers which then project them topographically to the deeper layers. The chosen target position blocks interruptions from other targets during its execution. When auditory or planned target positions and visually reactive target positions agree, then map learning is reinforced. When the auditory or planned target positions and visually reactive target positions disagree, then learning between these different representations is suppressed, and the distracting target is prevented from interrupting the saccade. Open circles are sources of inhibition from the substantia nigra pars reticulata, or SNr, of the basal ganglia which opens gates in the SC to enable targets at those positions to be performed. Rostral migration of activity in the spreading wave layer from its original position erodes feedback excitation to the burst cell layer at which visually reactive targets are stored, thereby leading to decay of activity at the peak decay layer, and justifying its name. [Reprinted with permission from [228] published in Wiley.]
This map enables visual, auditory, and planned movement commands to compete for attention, leading to selection of a winning position that controls where the next saccadic eye movement will go. Such map learning may be viewed as a kind of attentive motor category learning.
Grossberg, Palma, and Versace [227] extend this analysis to model how acetylcholine plays a role in SC map learning that is homologous to its role in regulating vigilance control during the learning of ART recognition categories, thereby establishing a mechanistic link between attention, learning, and cholinergic modulation during decision making within both cognitive and motor systems. The article also explains mechanistic homologs between the mammalian superior colliculus and the avian optic tectum [234, 235, 236], leading to predictions about how multimodal map learning may occur in the mammalian and avian brain and how such learning may be modulated by acetycholine.
These results show how ART dynamics help to carry out self-stabilizing category learning, modulated by acetylcholine vigilance control, in all neocortical regions as well as in subcortical circuits devoted to movement control.
Many different behaviors have been linked to attentive resonances in specific parts of the brain, as reviewed in [17, 18]. Several of these resonances and their attentional substrates are summarized in Table 1, as part of the general prediction that “all conscious states are resonant states”. Given that each kind of resonance activates some form of top-down attention and learning, a fundamental link is hereby shown between the CLEARS processes of Consciousness, Learning, Expectation, Attention, Resonance, and Synchrony.
The resonances in Table 1 may all be described using familiar words from daily language. That is true because each of them includes internal representations of external qualia, like brightness and color, or internal qualia, like hunger and pain, which become conscious during the resonance. Some functionally important resonances do not include internal representations of qualia, are not conscious, and thus do not have readily available names from day-to-day language.
For example, parietal-prefrontal resonances are predicted to trigger the selective opening of basal ganglia gates to enable the read out of context-appropriate actions [238, 240, 241]. Entorhinal-hippocampal resonances are predicted to dynamically stabilize the learning of entorhinal grid cells and hippocampal place cells that represent an animal’s current position during spatial navigation [242, 243, 244, 245].
For example, the TELOS model in Fig. 41 includes a parietal-prefrontal feedback loop between the frontal eye fields, or FEF, and the posterior parietal cortex, or PPC, that focuses spatial attention within the PPC on target positions in space to which saccadic eye movements will be directed. Additional interactions between the FEF and the basal ganglia, or BG, regulate the opening of gates in brain regions like the superior colliculus, or SC, that code these positions, and thereby release saccadic eye movements to foveate them.
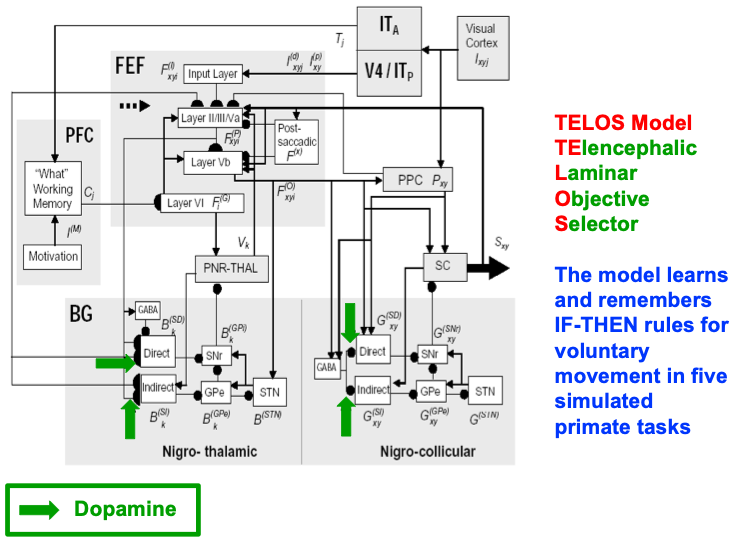 Fig. 41.
Fig. 41.The TELOS, or Telencephalic, Laminar, Objective,
Selector, model is a laminar model that simulates interactions of the
basal ganglia, or BG, with the frontal eye fields, or FEF, prefrontal cortex, or
PFC, and superior colliculus, or SC. Separate gray-shaded blocks highlight the
major anatomical regions whose roles in planned and reactive saccade generation
are explained and simulated in the model. Excitatory links are shown as
arrowheads, inhibitory as filled-in disks. Filled semi-circles terminate
corticostriatal and corticocortical pathways that can adapt due to learning,
which is modulated by reinforcement-related dopaminergic signals (green arrows).
In the FEF block, Roman numerals I-VI label cortical layers; Va and Vb,
respectively, are superficial and deep layer V. The BG decide which plan to
execute and send a disinhibitory gating signal that allows thalamic activation
V
The GridPlaceMap model in Fig. 42 includes an entorhinal-hippocampal feedback loop that dynamically stabilizes the learning of entorhinal grid cells and hippocampal place cells, while focusing attention upon the stripe cells, grid cells, and place cells that represent an animal’s current position in space. This loop provides a computational explanation of the hypothesis in the title of [243] that “Increased attention to spatial context increases both place field stability and spatial memory”.
 Fig. 42.
Fig. 42.Macrocircuit of GridPlaceMap model interactions within and between the entorhinal cortex (EC) and hippocampal cortex (DG/CA3 and CA1) to show how entorhinal grid cells and hippocampal place cells can be learned via a hierarchy of self-organizing maps in response to angular head velocity and linear velocity path integration signals while an animal navigates an environment. A resonant feedback loop between stripe cells, grid cells, and place cells is closed by top-down attentive feedback signals (red descending arrows) that dynamically stabilizes learning while focusing attention upon an animal’s current positional representation. [Adapted from with permission from [239] published in Wiley.]
Because each of these resonances does not include qualia, even though they do include resonant feedback loops that focus attention upon their respective representations, they do not support a reportable conscious state. That is why, although it is predicted that “all conscious states are resonant states”, it is not predicted that “all resonant states are conscious states”.
This article shows how multiple types of attention are incorporated into the CLEARS processes of Consciousness, Learning, Expectation, Attention, Resonance, and Synchrony that take place in perceptual, cognitive, affective, and motor systems throughout our brains. These processes enable us to continue learning about our unique and always changing experiences throughout life, while incorporating them into an emerging sense of self that defines our identities as human beings and supports all of our interactions with other individuals and the societies in which we live.
The author is the sole contributor to this article.
None.
There are no external funding sources for this article.
The author has no conflicts of interest.