1. Introduction
Analysis of the activities and properties of chemical compounds
is important not only for chemical science but also for biological science
because chemical compounds play important roles in metabolic and
many other pathways.
Computational prediction of chemical activities from their structural data
has been studied for several decades under the name of
quantitative structure activity relationship (QSAR) [1].
In addition to traditional regression-based methods,
various machine learning methods have been applied to QSAR [2, 3].
Recently, neural networks and deep-learning technologies have extensively
been applied to QSAR [4].
Inference of chemical structures with
desired chemical activities under some constraints is also important
because of its potential applications to drug design, and
the problem has been studied under the name of
inverse quantitative structure activity relationship (inverse QSAR).
Chemical compounds are commonly represented by undirected graphs called
chemical graphs
in which vertices and edges correspond to atoms and chemical bonds,
respectively.
Due to the difficulty of directly handling
chemical graphs in both QSAR and
inverse QSAR, chemical compounds are usually represented
as vectors of integer or real numbers,
which are called descriptors in chemoinformatics and
correspond to feature vectors in machine learning.
In inverse QSAR, one major approach is
to first infer feature vectors from given chemical activities and constraints,
and then reconstruct chemical structures from
these feature vectors [5, 6, 7].
However, the reconstruction itself is not an easy task
because the number of possible chemical graphs is huge.
For example, the number of
chemical graphs with up to 30 atoms (vertices)
C, N, O, and S
may exceed [8].
Indeed, the problem to infer a chemical graph from a given feature vector
is known as a computationally difficult problem (precisely,
NP-hard)
except for some simple cases [9].
Most existing methods for inverse QSAR
do not guarantee exact or optimal solutions due to these inherent difficulties.
Recently, artificial neural networks (ANNs), in particular,
graph convolutional networks [10] are extensively used
for inverse QSAR.
For example, recurrent neural networks [11, 12],
variational autoencoders [13],
grammar variational autoencoders [14],
invertible flow models [15, 16],
and generative adversarial networks [17]
have been applied.
However, these methods do not yet guarantee exact or optimal solutions.
Akutsu and Nagamochi [18] proved that
the computation process of a given ANN can be simulated as
a mixed integer linear programming (MILP).
Based on this result,
a novel framework for inferring a set of chemical graphs has been developed
[19, 20],
which is illustrated in Fig. 1.
This framework consists of two phases.
In the first phase,
it constructs a prediction function and
in the second phase,
it infers a chemical graph.
There are three stages in the first phase of the framework.
In Stage 1, a chemical property and a class
of graphs are selected, and a property function
is defined so that is the value of for a compound .
Then we collect a data set of chemical graphs in
such that is available for every .
In Stage 2, a feature function
for a positive integer is introduced.
In Stage 3, a prediction function is constructed
with an ANN that,
given a vector ,
returns a value
so that serves as a predicted value
to of for each .
Given a target chemical value ,
the second phase consists the next two phases
to infer chemical graphs
with .
A feature function and a prediction function are obtained in the first phase,
and we call an additional constraint on the substructures of target chemical graphs
a topological specification.
In Stage 4, the following two MILP formulations are designed:
- MILP
with a set of linear constraints on variables and
(and some other auxiliary variables)
simulates the process of computing from a vector ; and
- MILP
with a set of linear constraints on variable and
a variable vector that represents a chemical graph
(and some other auxiliary variables)
simulates the process of computing from a chemical graph and chooses a chemical graph that satisfies the given topological specification
.
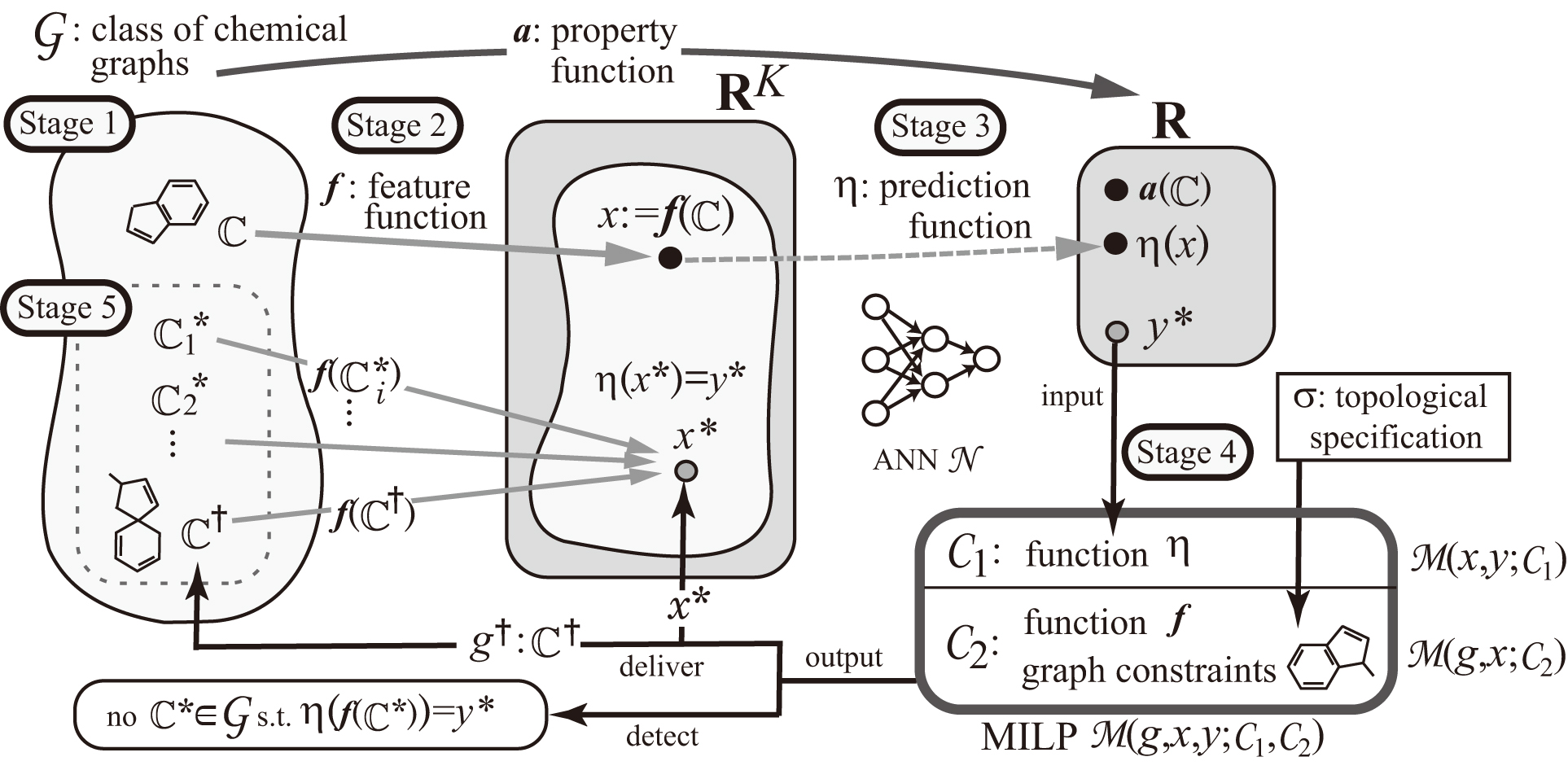 Fig. 1.
Fig. 1.
An illustration of a framework for inferring
a set of chemical graphs .
Given a target value , the combined
MILP is solved
to find a feature vector
and a chemical graph that satisfies the specification
such that and
(where if the MILP is infeasible then this suggests that
such a desired chemical graph does not exist).
In Stage 5, by using the inferred chemical graph ,
we generate other chemical graphs
such that .
Stage 4 MILP formulations to infer chemical graphs with
cycle index 0, 1 and 2 are proposed in [20, 21, 22, 23],
respectively,
but no sophisticated topological specification
was available yet.
A restricted class of acyclic graphs
that is characterized by an integer , called
a “branch-parameter” is introduced by Azam et al. [21].
This restricted class still covers most of the acyclic
chemical compounds in the database.
Akutsu and Nagamochi [24]
extended the idea to define a restricted class of cyclic graphs,
called “-lean cyclic graphs”
and introduced a set of flexible rules for describing a topological specification.
Tanaka et al. [25] used a decision tree instead of ANNs
to construct a prediction function in Stage 3 in the framework
and an MILP
that simulates the computation process of a decision tree.
Recently Shi et al. [26] proposed a new model to deal with an arbitrary graph
in the framework
called a two-layered model to represent
the feature of a chemical graph.
Also, the set of rules for describing a topological specification in [27] was refined
so that a prescribed structure
can be included in both of the acyclic and cyclic parts of a chemical graph .
In this model, a chemical graph with an integer ,
we consider two parts, namely,
the exterior and the interior of the hydrogen-suppressed graph that is obtained
by removing hydrogen from .
The exterior consists of maximal acyclic induced subgraphs with height
at most in and
the interior is the connected subgraph of
obtained by excluding the exterior.
Shi et al. [26] also defined
a feature vector of a chemical graph as a combination of the frequency of adjacent atom pairs in the interior and
the frequency of chemical acyclic graphs among the set of chemical rooted trees
rooted at interior-vertices .
Recently, Tanaka et al. [25]
extended the model in order to directly treat a chemical graph with hydrogens
so that
the feature of the exterior can be represented with more variety of chemical rooted trees.
The contribution of this paper is as follows.
Firstly, we make a slight modification to a model of chemical graphs
proposed by Tanaka et al. [25]
so that we can treat a chemical element with multi-valence such as sulfur S
and a chemical graph with cations and anions.
Then, we consider the prediction function.
One of the most important factors in the framework is
the quality of a prediction function constructed in Stage 3.
Also, overfitting is pointed out as a major issue in ANN-based approaches
for QSAR because many parameters need to be optimized for ANNs [4].
In this paper, to construct a prediction function in Stage 3, we use linear regression
instead of ANNs or decision trees.
A learning algorithm for an ANN may not find a set of weights
and biases that minimizes the error function since
the algorithm simply iterates modification of the current weights and biases
until it terminates at a local minimum value,
and linear regression is much simpler than ANNs and decision trees and
thereby we regard the performance of a prediction function by linear regression
as the basis for other more sophisticated machine learning methods.
In this paper, we derive an MILP formulation in Stage 4
to simulate the computation process of a prediction function by linear regression.
For an MILP formulation
that represents a feature function and a specification in Stage 4,
we can use the same formulation proposed by Tanaka et al. [25]
with a slight modification
(the detail of the MILP can be found
in Supplementary Material).
In Stage 5,
we can also use the dynamic programming algorithm
due to Tanaka et al. [25]
with a slight modification to generate target chemical graphs and the details
are omitted in this paper.
We implemented the framework based on the refined two-layered model
and a prediction function by linear regression.
The results of our computational experiments
reveal a set of chemical properties to which
a prediction function constructed by linear regression on our feature function
performs well, in comparison with ANNs in our previous work.
We also observe that
chemical graphs
with up to 50 non-hydrogen atoms can be inferred by the proposed method.
The paper is organized as follows.
Section 2 introduces some notions and terminologies on graphs,
modeling of chemical compounds and our choice of descriptors.
Section 3 describes our modification to the two-layered model.
Section 4 reviews the idea of linear regression
and formulates an MILP
that simulates the computing process of
a prediction function constructed by linear regression.
Section 5 reports the results of some computational
experiments conducted for 18 chemical properties such as
vapor density and
optical rotation.
Section 6 gives conclusions with future work.
Some technical details are given in Supplementary Material.
2. Preliminary
In this section, we review some notions and terminologies related to graphs,
modeling of chemical compounds introduced by
Tanaka et al. [25] and our choice of descriptors.
Let , , and
denote the sets of reals, non-negative reals,
integers and non-negative integers, respectively.
For two integers and , let denote the set of
integers with .
Graph
Given a graph , let and denote the sets
of vertices and edges, respectively.
For a subset (resp., of
a graph ,
let (resp., ) denote the graph obtained from
by removing the vertices in (resp., the edges in ),
where we remove all edges incident to a vertex in in .
An edge subset in a connected graph is called
separating (resp., non-separating)
if becomes disconnected
(resp., remains connected).
The rank of a connected graph
is defined to be the minimum of an edge subset
such that contains no cycle,
where .
Observe that holds
for any non-separating edge subset .
An edge in a connected graph
is called a bridge if is separating, i.e.,
consists of two connected graphs containing vertex , .
For a connected cyclic graph , an edge is called a core-edge if
it is in a cycle of or is a bridge such that
each of the connected graphs , , of contains a cycle.
A vertex incident to a core-edge is called a core-vertex of .
A path with two end-vertices and is called a -path.
A vertex designated in a graph is called a root.
In this paper, we designate at most two vertices as roots,
and denote by the set of roots of .
We call a graph rooted (resp., bi-rooted)
if (resp., ),
where we call unrooted if .
For a graph possibly with roots,
a leaf-vertex is defined to be a non-root vertex
with degree 1.
Call the edge incident to a leaf vertex a leaf-edge,
and denote by and
the sets of leaf-vertices and leaf-edges in , respectively.
For a graph or a rooted graph ,
we define graphs obtained from
by removing the set of leaf-vertices times so that
(1)
where we call a vertex
a leaf -branch and
we say that a vertex has
in .
The of a rooted tree is defined
to be the maximum of of a vertex .
For an integer , we call a rooted tree -lean if has at most one leaf -branch.
For an unrooted cyclic graph , we regard that the set of non-core-edges in induces
a collection of trees each of which is rooted at a core-vertex,
where we call -lean if each of the rooted trees in
is -lean.
Modeling of Chemical Compounds
We introduce a set of chemical elements such as
H (hydrogen),
C (carbon), O (oxygen), N (nitrogen) and so on to represent a chemical compound.
To distinguish a chemical element with multiple valences such as S (sulfur),
we denote a chemical element with a valence by ,
where we do not use such a suffix
for a chemical element with a unique valence.
Let be a set of chemical elements .
For example,
.
Let be a valence function.
For example, , , , ,
, and .
For each chemical element ,
let denote the mass of .
To represent a chemical compound, we use a chemical graph
introduced by
Tanaka et al. [25],
which
is defined to be
a tuple of
a simple, connected undirected graph and
functions and .
The set of atoms and the set of bonds in the compound
are represented by the vertex set and the edge set , respectively.
The chemical element assigned to a vertex
is represented by and
the bond-multiplicity between two adjacent vertices
is represented by of the edge .
We say that two tuples are
isomorphic if they admit an isomorphism ,
i.e., a bijection
such that
.
When is rooted at a vertex ,
are
rooted-isomorphic (r-isomorphic) if
they admit an isomorphism such that .
For a notational convenience, we use
a function
for a chemical graph
such that means the sum of bond-multiplicities
of edges incident to a vertex ; i.e.,
(2)
for each vertex .
For each vertex ,
define the electron-degree to be
(3)
For each vertex ,
let denote the number of vertices
adjacent to the vertex in .
For a chemical graph ,
let ,
denote the set vertices such that in
and define the hydrogen-suppressed chemical graph
to be the graph obtained from by
removing all the vertices .
3. Two-layered Model
This section reviews the idea of the two-layered model introduced by
Shi et al. [26], and
describes our modifications to the model.
Let be a chemical graph
and be an integer, which is called a branch-parameter.
A two-layered model of
introduced by Shi et al. [26] is a partition of
the hydrogen-suppressed chemical graph into
an “interior” and an “exterior” in the following way.
We call a vertex
(resp., an edge of
an exterior-vertex (resp., exterior-edge) if
(resp., is incident to an exterior-vertex)
and denote the sets of exterior-vertices and exterior-edges
by and , respectively
and denote and
, respectively.
We call a vertex in (resp., an edge in )
an interior-vertex (resp., interior-edge).
The set of exterior-edges forms
a collection of connected graphs each of which is
regarded as a rooted tree rooted at
the vertex with the maximum .
Let denote
the set of these chemical rooted trees in .
The interior of is defined to be the subgraph
of .
Fig. 2
illustrates an example of a hydrogen-suppressed chemical graph .
For a branch-parameter ,
the interior of the chemical graph in Fig. 2
is obtained by removing the set of vertices with degree 1 times; i.e.,
first remove
the set of vertices of degree 1 in
and then remove the set
of vertices of degree 1 in ,
where the removed vertices become the exterior-vertices of .
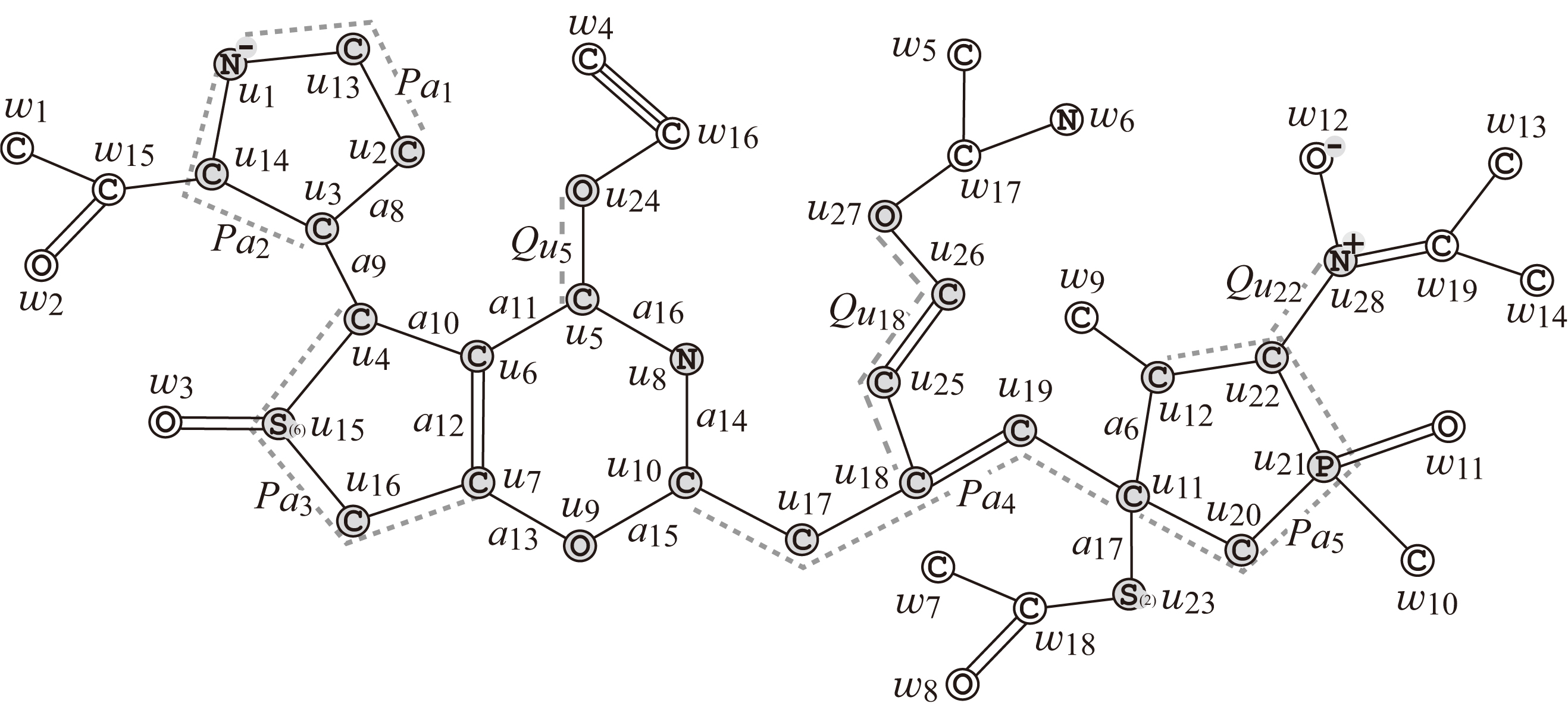 Fig. 2.
Fig. 2.
An illustration of a hydrogen-suppressed chemical graph
obtained from a chemical graph with
by removing all the hydrogens,
where for ,
and
For each interior-vertex ,
let denote the chemical tree rooted at
(where possibly consists of vertex )
and
define the -fringe-tree
to be
the chemical rooted tree obtained from by putting back
the hydrogens originally attached to in .
Let denote the set of -fringe-trees
.
Fig. 3 illustrates
the set of the 2-fringe-trees
of the example
in Fig. 2.
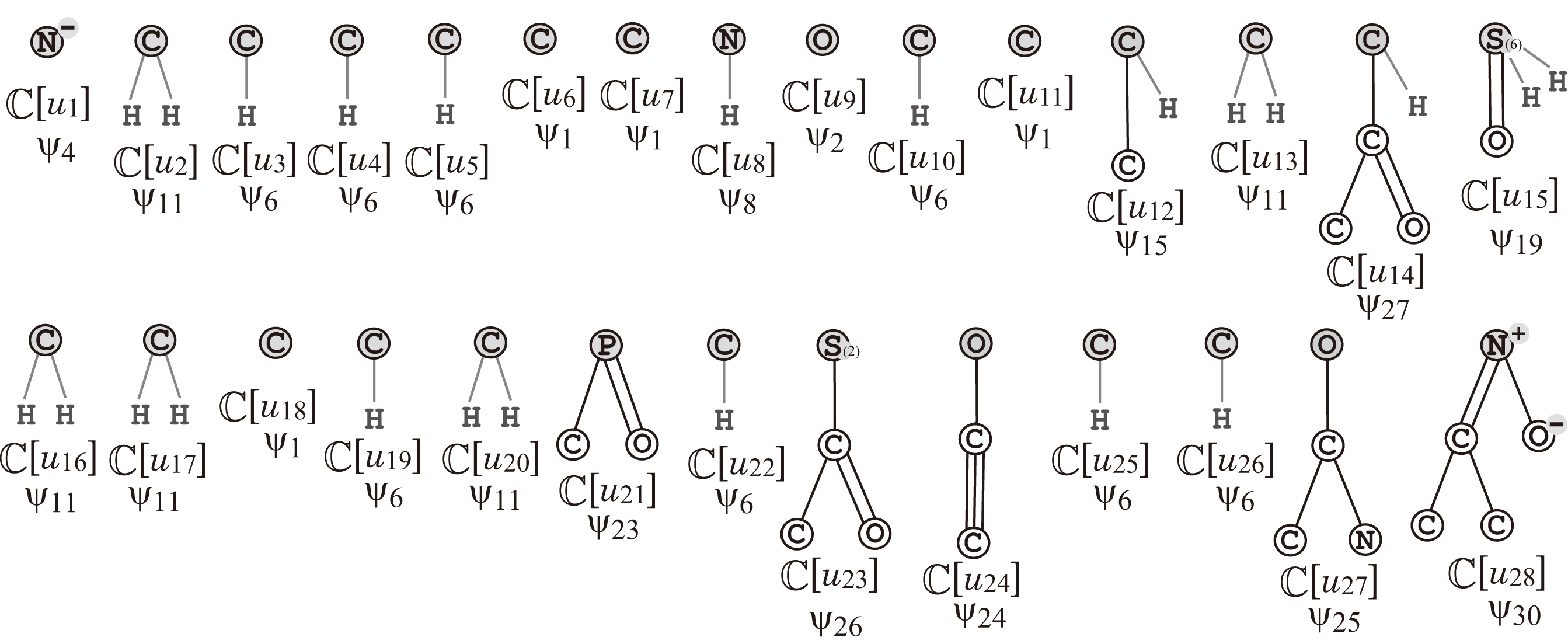 Fig. 3.
Fig. 3.
The set of the example
in Fig. 2,
where the root of each tree is depicted with a gray circle and
the hydrogens attached to non-root vertices are omitted in the figure.
Feature Function
We extend the feature function
of a chemical graph introduced by Tanaka et al. [25].
The feature of an interior-edge
such that , ,
, and is represented by
a tuple , which is called the edge-configuration
of the edge , where
we call the tuple
the adjacency-configuration of the edge .
For an integer , a feature vector of a chemical graph
is defined by a feature function that consists of descriptors.
We call the feature space.
Tanaka et al. [25]
defined a feature vector
to be a combination of the frequency
of edge-configurations of the interior-edges and
the frequency of chemical rooted trees among the set
of chemical rooted trees over all interior-vertices .
In this paper, we introduce the rank and the adjacency-configuration of leaf-edges
as new descriptors in a feature vector of a chemical graph.
See Supplementary Material for a full description of descriptors used in Stage 2 of the framework.
Topological Specification
A topological specification is described
as a set of the following rules proposed by Shi et al. [26]
and modified by Tanaka et al. [25]:
(i) a seed graph as an abstract form of a target chemical graph ;
(ii) a set of chemical rooted trees as candidates
for a tree rooted at each exterior-vertex in ;
and
(iii) lower and upper bounds on the number of components
in a target chemical graph such as chemical elements,
double/triple bounds and the interior-vertices in .
Fig. 4a,b
illustrate examples of a seed graph and
a set of chemical rooted trees, respectively.
Given a seed graph ,
the interior of a target chemical graph is constructed
from by replacing some edges
with paths between the end-vertices
and and by attaching new paths to some vertices .
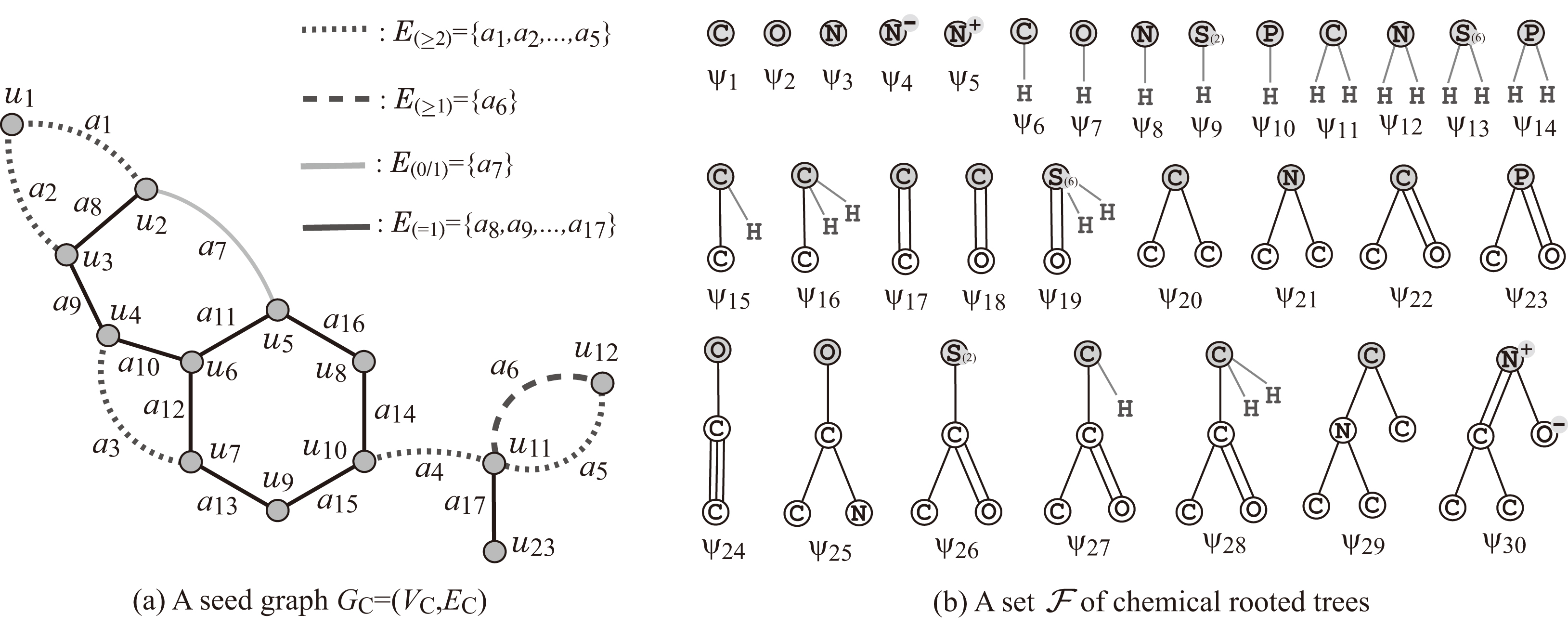 Fig. 4.
Fig. 4.
(a) An illustration of a seed graph with
where the vertices in are depicted with gray circles,
the edges in are depicted with dotted lines,
the edges in are depicted with dashed lines,
the edges in are depicted with gray bold lines and
the edges in are depicted with black solid lines;
(b) A set of 30 chemical rooted trees
, where the root of each tree is depicted with a gray circle,
where the hydrogens attached to non-root vertices are omitted in the figure.
For example, a chemical graph
in Fig. 2 is constructed
from the seed graph in Fig. 4a
as follows.
- First replace five edges
and in
with new paths
,
,
,
and
, respectively
to obtain a subgraph of .
- Next attach to this graph three new paths
,
and
to obtain
the interior of in Fig. 2.
- Finally attach to the interior 28 trees selected from the set
and assign chemical elements and bond-multiplicities in the interior
to obtain a chemical graph in Fig. 2.
In Fig, 3,
is selected for , .
Similarly
for ,
for ,
for ,
,
for ,
for , ,
for ,
for ,
for ,
for ,
for ,
for ,
for
and
for .
Our definition of a topological specification is analogous with the one by
Tanaka et al. [25]
except for a necessary modification due to the introduction
of multiple valences of chemical elements, cations and anions
(see Supplementary Material
for a full description of topological specification).
4. Linear Regressions
For an integer and a vector , the -th entry of
is denoted by .
Let be a data set of chemical graphs with
an observed value ,
where we denote by
for an indexed graph .
Let be a feature function that maps a chemical graph
to a vector
where we denote by
for an indexed graph .
For a prediction function ,
define an error function
(4)
and define the coefficient of determination
to be
(5)
For a feature space , a hyperplane is denoted by
a pair of a vector and a real .
Given a hyperplane ,
a prediction function is defined by setting
(6)
We wish to find a hyperplane that minimizes the error function
.
In many cases, a feature vector contains descriptors that do not play
an essential role in constructing a good prediction function.
When we solve the minimization problem, the entries for some descriptors
in the resulting hyperplane become zero, which means that these descriptors were
not necessarily important for finding a prediction function .
It is proposed that solving the minimization with an additional penalty term to the error function
often results in more number of entries , reducing a set of descriptors
necessary for defining a prediction function .
For an error function with such a penalty term,
a Ridge function [28]
and a Lasso function
[29]
are known, where is a given real number.
Given a prediction function ,
we can simulate a process of computing the output for an input
as an MILP in the framework.
By solving such an MILP for a specified target value ,
we can find a vector such that .
Instead of specifying a single target value , we use
lower and upper bounds
on the value of a chemical graph to be inferred.
We can control the range between and
for searching a chemical graph
by setting and to be close or different values.
A desired MILP is formulated as follows.
:
An MILP formulation for the inverse problem to prediction function.
constants:
- A hyperplane with and ;
- Real values such that ;
- A set of indices such that
the -th descriptor is always an integer;
- A set of indices such that
the -th descriptor is always non-negative;
- , : lower and upper bounds on the -th descriptor;
variables:
- Non-negative integer variable , ;
- Integer variable ;
- Non-negative real variable ;
- Real variable ;
constraints:
(7)
objective function: none.
The number of variables and constraints in the above MILP formulation is .
It is not difficult to see that the above MILP is an NP-hard problem.
The entire MILP for Stage 4 consists of the two MILPs
and
with no objective function.
The latter represents the computation process of our feature function and
a given topological specification.
See Supplementary Material
for the details of MILP .
5. Results
We implemented our method of Stages 1 to 5
for inferring chemical graphs under a given topological specification and
conducted experiments to evaluate the computational efficiency.
We executed the experiments on a PC with
Processor: Core i7-9700 (3.0 GHz; 4.7 GHz at the maximum) and
Memory: 16 GB RAM DDR4.
Results on Phase 1.
We have conducted experiments of linear regression for
37 chemical properties among which
we report the following 18 properties to which the test
coefficient of determination
attains at least 0.8:
octanol/water partition coefficient (Kow),
heat of combustion (Hc),
vapor density (Vd),
optical rotation (OptR),
electron density on the most positive atom (EDPA),
melting point (Mp),
heat of atomization (Ha),
heat of formation (Hf),
internal energy at 0K (U0),
energy of lowest unoccupied molecular orbital (Lumo),
isotropic polarizability (Alpha),
heat capacity at 298.15K (Cv),
solubility (Sl),
surface tension (SfT),
viscosity (Vis),
isobaric heat capacities in liquid phase (IhcLiq),
isobaric heat capacities in solid phase (IhcSol) and
lipophilicity (Lp).
We used data sets provided by HSDB from PubChem [30]for Kow, Hc, Vd and OptR, M. Jalali-Heravi and M. Fatemi [31] for EDPA, Roy and Saha [32] for Mp, Ha and Hf, MoleculeNet [33] for U0, Lumo, Alpha, Cv and Sl, Goussard et al. [34] for SfT and Vis, R. Naef [35] for IhcLiq and IhcSol, and Figshare [36] for Lp.
Properties U0, Lumo, Alpha and Cv share a common original data set
with more than 130,000 compounds, and
we used a set of 1,000 graphs randomly selected from
as a common data set of these four properties
in this experiment.
Stages 1, 2 and 3 in Phase 1 are implemented as follows.
Stage 1.
We set a graph class to be
the set of all chemical graphs with any graph structure,
and set a branch-parameter to be 2.
For each of the properties,
we first select a set of chemical elements
and then collect a data set on chemical graphs
over the set of chemical elements.
During construction of the data set ,
chemical compounds that do not satisfy
one of the following are eliminated: the graph is connected,
the number of non-hydrogen neighbors of each atom is
at most four,
and the number of carbon atoms is at least four.
Table 1 shows
the size and range of data sets that
we prepared for each chemical property in Stage 1,
where we denote the following:
- : the set of elements used in the data set ;
is one of the following 11 sets:
;
;
;
;
;
;
;
;
;
; and
,
where for a chemical element and an integer
means that a chemical element with valence .
- : the size of data set over
for the property .
- :
the minimum and maximum values of the number
of non-hydrogen atoms in
compounds in .
- : the minimum and maximum values
of for over compounds in .
- :
the number of different edge-configurations
of interior-edges over the compounds in .
- : the number of non-isomorphic chemical rooted trees
in the set of all 2-fringe-trees in the compounds in .
- : the number of descriptors in a feature vector .
Table 1.Results in Phase 1.
|
|
|
|
|
|
|
|
|
|
test |
| Kow |
|
684 |
4, 58 |
–7.5, 15.6 |
25 |
166 |
223 |
|
80.3 |
0.953 |
| Kow |
|
899 |
4, 69 |
–7.5, 15.6 |
37 |
219 |
303 |
|
112.1 |
0.927 |
| Hc |
|
255 |
4, 63 |
49.6, 35099.6 |
17 |
106 |
154 |
|
19.2 |
0.946 |
| Hc |
|
282 |
4, 63 |
49.6, 35099.6 |
21 |
118 |
177 |
|
20.5 |
0.951 |
| Vd |
|
474 |
4, 30 |
0.7, 20.6 |
21 |
160 |
214 |
|
3.6 |
0.927 |
| Vd |
|
551 |
4, 30 |
0.7, 20.6 |
24 |
191 |
256 |
|
8.0 |
0.942 |
| OptR |
|
147 |
5, 44 |
–117.0, 165.0 |
21 |
55 |
107 |
|
39.2 |
0.823 |
| OptR |
|
157 |
5, 69 |
–117.0, 165.0 |
25 |
62 |
123 |
|
41.7 |
0.825 |
| EDPA |
|
52 |
11, 16 |
0.80, 3.76 |
9 |
33 |
64 |
|
10.9 |
0.999 |
| Mp |
|
467 |
4, 122 |
–185.33, 300.0 |
23 |
142 |
197 |
|
82.5 |
0.817 |
| Ha |
|
115 |
4, 11 |
1100.6, 3009.6 |
8 |
83 |
115 |
|
39.0 |
0.997 |
| Hf |
|
82 |
4, 16 |
30.2, 94.8 |
5 |
50 |
74 |
|
34.0 |
0.987 |
| U0 |
|
977 |
4, 9 |
–570.6, –272.8 |
59 |
190 |
297 |
|
246.7 |
0.999 |
| Lumo |
|
977 |
4, 9 |
–0.11, 0.10 |
59 |
190 |
297 |
|
133.9 |
0.841 |
| Alpha |
|
977 |
4, 9 |
50.9, 99.6 |
59 |
190 |
297 |
|
125.5 |
0.961 |
| Cv |
|
977 |
4, 9 |
19.2, 44.0 |
59 |
190 |
297 |
|
165.3 |
0.961 |
| Sl |
|
915 |
4, 55 |
–11.6, 1.11 |
42 |
207 |
300 |
|
130.6 |
0.808 |
| SfT |
|
247 |
5, 33 |
12.3, 45.1 |
11 |
91 |
128 |
|
20.9 |
0.804 |
| Vis |
|
282 |
5, 36 |
–0.64, 1.63 |
12 |
88 |
126 |
|
16.3 |
0.893 |
| IhcLiq |
|
770 |
4, 78 |
106.3, 1956.1 |
23 |
200 |
256 |
|
82.2 |
0.987 |
| IhcLiq |
|
865 |
4, 78 |
106.3, 1956.1 |
29 |
246 |
316 |
|
139.1 |
0.986 |
| IhcSol |
|
581 |
5, 70 |
67.4, 1220.9 |
33 |
124 |
192 |
|
75.9 |
0.985 |
| IhcSol |
|
668 |
5, 70 |
67.4, 1220.9 |
40 |
140 |
228 |
|
86.7 |
0.982 |
| Lp |
|
615 |
6, 60 |
–3.62, 6.84 |
32 |
116 |
186 |
|
98.5 |
0.856 |
| Lp |
|
936 |
6, 74 |
–3.62, 6.84 |
44 |
136 |
231 |
|
130.4 |
0.840 |
Stage 2.
The newly defined
feature function
in our chemical model without suppressing hydrogen in Section 3 is used.
We standardize the range of each descriptor and
the range
of property values .
Stage 3.
For each chemical property , we select a penalty value
in the Lasso function
from 36 different values from 0 to 100
by conducting linear regression as a preliminary experiment.
We conducted an experiment in Stage 3 to evaluate the performance
of the prediction function based on cross-validation.
For a property ,
an execution of a cross-validation consists of five trials of
constructing a prediction function as follows.
First partition the data set
into five subsets , randomly.
For each , the -th trial
constructs a prediction function by conducting
a linear regression with the penalty term
using the set as a training data set.
We used scikit-learn version 0.23.2 with Python 3.8.5 for executing linear regression
with Lasso function.
For each property, we executed ten cross-validations and
we show the median of test
over all ten cross-validations.
Recall that a subset of descriptors is selected in linear regression with Lasso function
and let denote the average number of selected descriptors over all 50 trials.
The running time per trial in a cross-validation was at most one second.
Table 1 shows the results on Stages 2 and 3,
where we denote the following:
- : the penalty value in the Lasso function selected
for a property , where means .
- : the average of the number of descriptors selected in the linear regression
over all 50 trials in ten cross-validations.
- test : the median of test over all 50 trials
in ten cross-validations.
Recall that the adjacency-configuration for leaf-edges was introduced
as a new descriptor in this paper.
Without including this new descriptor,
the test for property Vis was 0.790,
that for Lumo was 0.799 and that for Mp was 0.796,
while the test for each of the other properties in Table 1
was almost the same.
From Table 1, we observe that a relatively large number of properties
admit a good prediction function based on linear regression.
The number of descriptors used in linear regression is considerably small
for some properties.
For example of property Vd,
the four descriptors most frequently selected
in the case of are
the number of non-hydrogen atoms;
the number of interior-vertices with ;
the number of fringe-trees r-isomorphic to the chemical rooted tree
in Fig. 5; and
the number of leaf-edges with adjacency-configuration .
The eight descriptors most frequently selected in the case of
are
the number of non-hydrogen atoms;
the number of interior-vertices with ;
the number of exterior-vertices with ;
the number of interior-edges with edge-configuration ,
where and ; and
the number of fringe-trees r-isomorphic to the chemical rooted tree
in Fig. 5.
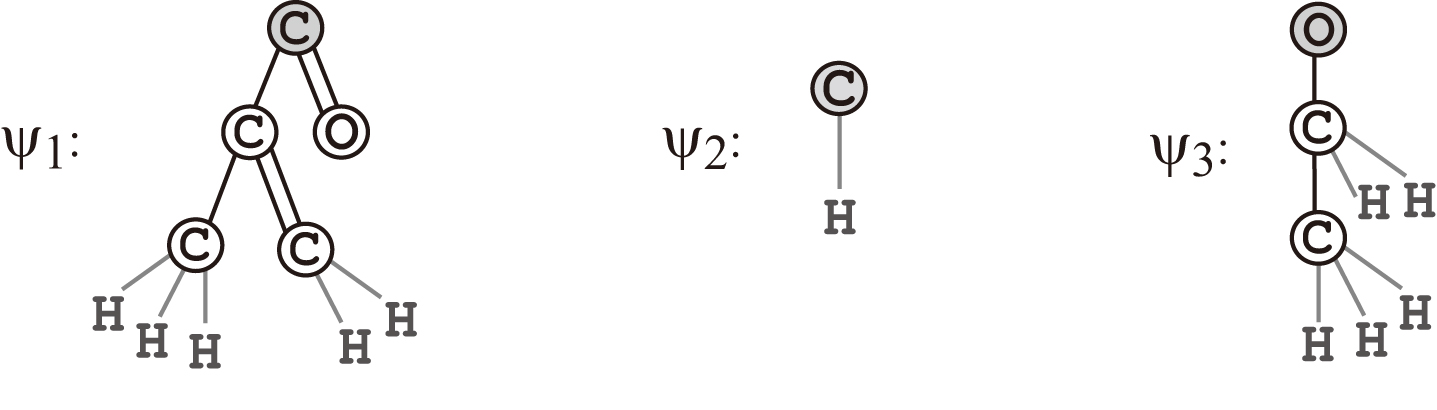 Fig. 5.
Fig. 5.
An illustration of chemical rooted trees
, and
that are selected in Lasso linear regression for constructing
a prediction function to property Vd, where the root is depicted with a gray circle.
For the 18 properties listed in Table 1, we used ANN to construct prediction
functions. For this purpose, we used our newly proposed feature vector and the experimental setup as
explained in Tanaka et al. [25]. From these computation experiments,
we observe that for the
properties Hc, Vd, Ha, Hf,
U0, Alpha and Cv, the test scores of
the prediction functions obtained by Lasso linear regression is at least 0.05 more than those obtained
by ANN. For the properties OptR, Sl and SfT,
the test scores of
the prediction functions obtained by ANN is at least 0.05 more than those obtained
by Lasso linear regression. For the other properties, the test scores obtained by
Lasso linear regression and ANN are comparable.
Results on Phase 2.
We used a set of seven instances
, ,
and based on seed graphs prepared by Shi et al. [26]
to execute Stages 4 and 5 in Phase 2.
We here present their seed graphs
(see Supplementary Material for the details of instances ,
, and ).
The seed graph of instance is
illustrated in Fig. 4a.
The seed graph (resp., ) of instances
and (resp., ) is illustrated
in Fig. 6.
 Fig. 6.
Fig. 6.
(i) Seed graph for and ;
(ii) Seed graph for ;
(iii) Seed graph for ;
(iv) Seed graph for .
Instance has been introduced by Shi et al. [26]
in order to infer a chemical graph such that
the core of is the same as the core of
chemical graph : CID 24822711 in Fig. 7a
and
the frequency of each edge-configuration in the non-core of
is the same as that of chemical graph : CID 59170444 illustrated
in Fig. 7b.
This means that the seed graph of
is the core of
which is indicated by a shaded area in Fig. 7a.
Instance has been introduced by Shi et al. [26]
in order to infer a monocyclic chemical graph such that
the frequency vector of edge-configurations in
is a vector obtained by merging those of two chemical graphs
: CID 10076784 and : CID 44340250
illustrated
in Fig. 7c,d, respectively.
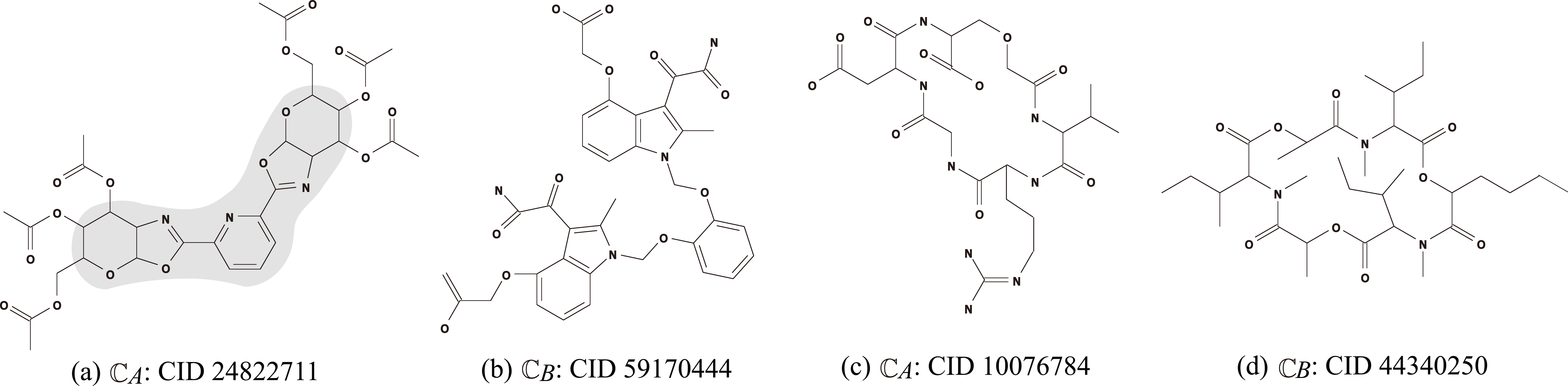 Fig. 7.
Fig. 7.
An illustration of chemical compounds
for instances and :
(a) : CID 24822711;
(b) : CID 59170444;
(c) : CID 10076784;
(d) : CID 44340250,
where hydrogens are omitted.
Stage 4.
We executed Stage 4 for five properties Hc, Vd, OptR, IhcLiq, Vis.
For the MILP formulation
in Section 4,
we use the prediction function
that attained the median test in Table 1.
We used
CPLEX version 12.10 to solve an MILP in Stage 4.
Tables 2,3,4,5,6 show
the computational results of the experiment
in Stage 4 for the five properties,
where we denote the following:
- :
lower and upper bounds ,
on the value of a chemical graph to be inferred;
- v (resp., c):
the number of variables (resp., constraints) in the MILP in Stage 4;
- I-time: the time (sec.) to solve the MILP in Stage 4;
- : the number of non-hydrogen atoms
in the chemical graph inferred in Stage 4; and
- : the number of interior-vertices in
the chemical graph inferred in Stage 4;
- : the predicted property value
of the chemical graph inferred
in Stage 4.
Table 2.Results of Stages 4 and 5 for Hc using Lasso linear regression.
| inst. |
|
v |
c |
I-time |
|
|
|
D-time |
-LB |
|
|
5950, 6050 |
9902 |
9255 |
4.6 |
44 |
25 |
5977.9 |
0.068 |
1 |
1 |
|
5950, 6050 |
9404 |
6776 |
1.7 |
36 |
10 |
6007.1 |
0.048 |
6 |
6 |
|
5950, 6050 |
11729 |
9891 |
16.7 |
50 |
25 |
6043.7 |
38.7 |
|
100 |
|
5950, 6050 |
11510 |
9894 |
16.3 |
47 |
25 |
6015.4 |
0.353 |
8724 |
100 |
|
5950, 6050 |
11291 |
9897 |
9.0 |
49 |
26 |
5971.6 |
0.304 |
84 |
84 |
|
13700, 13800 |
6915 |
7278 |
0.7 |
50 |
33 |
13703.3 |
0.016 |
1 |
1 |
|
13700, 13800 |
5535 |
6781 |
4.9 |
44 |
23 |
13704.7 |
0.564 |
|
100 |
Table 3.Results of Stages 4 and 5 for Vd using Lasso linear regression.
| inst. |
|
v |
c |
I-time |
|
|
|
D-time |
-LB |
|
|
16, 17 |
9481 |
9358 |
1.6 |
38 |
23 |
16.83 |
0.070 |
1 |
1 |
|
16, 17 |
9928 |
6986 |
1.5 |
35 |
12 |
16.68 |
0.206 |
48 |
48 |
|
21, 22 |
12373 |
10101 |
10.0 |
48 |
25 |
21.62 |
0.104 |
20 |
20 |
|
21, 22 |
12159 |
10104 |
6.5 |
48 |
25 |
21.95 |
3.65 |
|
100 |
|
21, 22 |
11945 |
10107 |
8.1 |
48 |
25 |
21.34 |
0.057 |
6 |
6 |
|
21, 22 |
7073 |
7438 |
0.7 |
50 |
34 |
21.89 |
0.016 |
1 |
1 |
|
17, 18 |
5693 |
6942 |
2.1 |
41 |
23 |
17.94 |
0.161 |
216 |
100 |
Table 4.Results of Stages 4 and 5 for OptR using Lasso linear regression.
| inst. |
|
v |
c |
I-time |
|
|
|
D-time |
-LB |
|
|
70, 71 |
8962 |
9064 |
3.5 |
40 |
23 |
70.1 |
0.061 |
1 |
1 |
|
70, 71 |
9432 |
6662 |
2.7 |
37 |
14 |
70.1 |
0.185 |
2622 |
100 |
|
70, 71 |
11818 |
9773 |
10.0 |
50 |
25 |
70.8 |
0.041 |
4 |
4 |
|
70, 71 |
11602 |
9776 |
10.2 |
50 |
25 |
70.2 |
0.241 |
60 |
60 |
|
70, 71 |
11386 |
9779 |
24.7 |
49 |
25 |
70.9 |
6.39 |
|
100 |
|
–112, –111 |
6807 |
7170 |
1.8 |
50 |
32 |
-111.9 |
0.016 |
1 |
1 |
|
70, 71 |
5427 |
6673 |
6.1 |
42 |
23 |
70.2 |
0.127 |
78768 |
100 |
Table 5.Results of Stages 4 and 5 for IhcLiq using Lasso linear regression.
| inst. |
|
v |
c |
I-time |
|
|
|
D-time |
-LB |
|
|
1190, 1210 |
10180 |
9538 |
3.9 |
48 |
26 |
1208.5 |
0.071 |
2 |
2 |
|
1190, 1210 |
10784 |
7191 |
2.4 |
35 |
14 |
1206.7 |
0.082 |
12 |
12 |
|
1190, 1210 |
13482 |
10302 |
14.1 |
47 |
25 |
1206.7 |
0.11 |
12 |
12 |
|
1190, 1210 |
13275 |
10301 |
9.0 |
49 |
27 |
1209.9 |
0.090 |
24 |
24 |
|
1190, 1210 |
13128 |
10306 |
16.5 |
50 |
25 |
1208.4 |
0.424 |
2388 |
100 |
|
1190, 1210 |
7193 |
7560 |
0.8 |
50 |
33 |
1196.5 |
0.016 |
1 |
1 |
|
1190, 1210 |
5813 |
7063 |
2.2 |
44 |
23 |
1198.8 |
5.63 |
|
100 |
Table 6.Results of Stages 4 and 5 for Vis using Lasso linear regression.
| inst. |
|
v |
c |
I-time |
|
|
|
D-time |
-LB |
|
|
1.25, 1.30 |
6847 |
8906 |
1.3 |
38 |
22 |
1.295 |
0.042 |
2 |
2 |
|
1.25, 1.30 |
7270 |
6397 |
2.5 |
36 |
15 |
1.272 |
0.155 |
140 |
100 |
|
1.85, 1.90 |
8984 |
9512 |
8.9 |
45 |
25 |
1.879 |
0.149 |
288 |
100 |
|
1.85, 1.90 |
8741 |
9515 |
16.2 |
45 |
26 |
1.880 |
0.137 |
4928 |
100 |
|
1.85, 1.90 |
8498 |
9518 |
8.1 |
45 |
25 |
1.851 |
0.13 |
660 |
100 |
|
2.75, 2.80 |
6813 |
7162 |
1.0 |
50 |
33 |
2.763 |
0.025 |
4 |
4 |
|
1.85, 1.90 |
5433 |
6665 |
2.7 |
41 |
23 |
1.881 |
0.138 |
4608 |
100 |
From Tables 2,3,4,5,6
we observe that an instance with a large number of variables and constraints
takes more running time than those with a smaller size in general.
We solved all instances in this experiment
with our MILP formulation in a few seconds to around 30 seconds.
Fig. 8a–e illustrate the chemical graphs inferred
from with
of Hc,
with of Vd,
with of OptR, with of IhcLiq, and
with of Vis,
respectively.
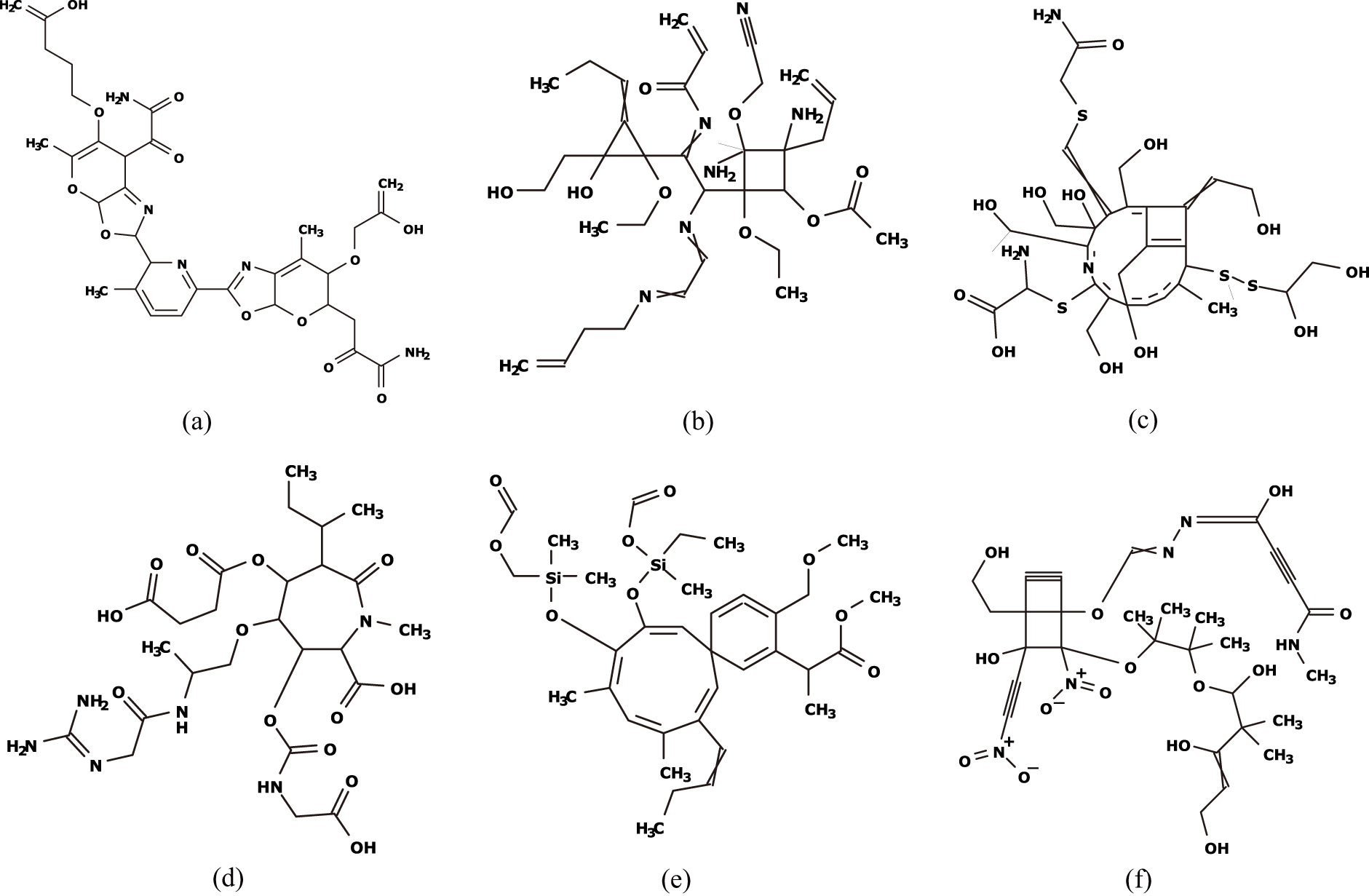 Fig. 8.
Fig. 8.
(a) with inferred
from with of Hc;
(b) with inferred
from with of Vd;
(c) with inferred
from with of OptR;
(d) with inferred
from with of IhcLiq;
(e) with inferred
from with of Vis;
(f) inferred
from with lower and upper bounds on
the predicted property value of property
Kow, Lp, Sl in Table 9.
Similarly, we executed Stage 4 for these seven instances
, ,
and for five properties Hc, Vd, OptR, IhcLiq, Vis
by using the prediction functions obtained by ANN.
We list the running time to solve MILP formulation for each of these instances in
Tables 7,8.
From the computation experiments, we observe that for many instances,
the running time is
significantly faster than that of Stage 4 based on ANN.
Table 7.Running time of Stage 4 for Hc, Vd and OptR using ANN.
|
Hc |
|
|
Vd |
|
|
OptR |
|
| inst. |
|
I-time |
inst. |
|
I-time |
inst. |
|
I-time |
|
13350, 13450 |
24.7 |
|
18, 19 |
18.1 |
|
62, 63 |
35.6 |
|
9650, 9750 |
13.5 |
|
13, 14 |
9.4 |
|
109, 110 |
15.5 |
|
16750, 16850 |
70.4 |
|
15, 16 |
40.9 |
|
23, 24 |
192.6 |
|
12350, 12450 |
87.0 |
|
20, 21 |
46.3 |
|
-2, -1 |
936.4 |
|
14250, 14350 |
70.9 |
|
22, 23 |
27.1 |
|
19, 20 |
63.9 |
|
10400, 10500 |
31.3 |
|
20, 21 |
20.5 |
|
86, 87 |
16.4 |
|
12500, 12600 |
44.3 |
|
18, 19 |
6.1 |
|
30, 31 |
31.8 |
Table 8.Running time of Stage 4 for IhcLiq and Vis using ANN.
|
IhcLiq |
|
|
Vis |
|
| inst. |
|
I-time |
inst. |
|
I-time |
|
980, 1000 |
56.6 |
|
1.85, 1.90 |
2.0 |
|
1000, 1020 |
40.4 |
|
1.95, 2.00 |
3.5 |
|
1130, 1150 |
71.6 |
|
1.85, 1.90 |
19.7 |
|
1240, 1260 |
45.0 |
|
2.35, 2.40 |
26.0 |
|
1240, 1260 |
105.7 |
|
2.50, 2.55 |
9.3 |
|
810, 830 |
9.7 |
|
3.90, 3.95 |
1.8 |
|
1100, 1120 |
25.8 |
|
3.30, 3.35 |
8.3 |
Inferring a chemical graph with target values in multiple properties
Once we obtained prediction functions for several properties ,
include MILP formulations for these functions
into a single MILP so as to
infer a chemical graph that satisfies given target values for
these properties at the same time.
As an additional experiment in Stage 4,
we inferred a chemical graph that has a desired predicted value
each of three properties Kow, Lp and Sl,
where we used the prediction function
for each property Kow, Lp, Sl constructed in
Stage 3.
Table 9 shows the result of Stage 4
for inferring a chemical graph
from instances , and
with ,
where we denote the following:
- : one of the three properties Kow, Lp and Slused in the experiment;
- :
lower and upper bounds
on the predicted property value
of property
Kow, Lp, Sl
for a chemical graph to be inferred;
- v (resp., c):
the number of variables (resp., constraints) in the MILP in Stage 4;
- I-time: the time (sec.) to solve the MILP in Stage 4;
- : the number of non-hydrogen atoms
in the chemical graph inferred in Stage 4;
- : the number of interior-vertices in
the chemical graph inferred in Stage 4; and
- : the predicted property value
of property
Kow, Lp, Sl
for the chemical graph inferred in Stage 4.
Table 9.Results of Stage 4 for instances
with specified target values of three properties Kow, Lp and Sl
using Lasso linear regression.
| inst. |
|
|
v |
c |
I-time |
|
|
|
|
Kow |
–7.50, –7.40 |
|
|
|
|
|
–7.41 |
|
Lp |
–1.40, –1.30 |
14574 |
11604 |
62.7 |
50 |
30 |
–1.33 |
|
Sl |
–11.6, –11.5 |
|
|
|
|
|
–11.52 |
|
Kow |
–7.40, –7.30 |
|
|
|
|
|
–7.38 |
|
Lp |
–2.90, –2.80 |
14370 |
11596 |
35.5 |
48 |
25 |
–2.81 |
|
Sl |
–11.6, –11.4 |
|
|
|
|
|
–11.52 |
|
Kow |
–7.50, –7.40 |
|
|
|
|
|
–7.48 |
|
Lp |
–0.70, –0.60 |
14166 |
11588 |
71.7 |
49 |
26 |
–0.63 |
|
Sl |
–11.4, –11.2 |
|
|
|
|
|
–11.39 |
Fig. 8f illustrates the chemical graph inferred
from with
,
and
for Kow, Lp and Sl, respectively.
Stage 5.
We executed Stage 5 to generate
more target chemical graphs ,
where a chemical graph is called a chemical isomer of
a target chemical graph of a topological specification
if and also satisfies the same topological specification .
We computed chemical isomers of
each target chemical graph inferred in Stage 4.
We executed an algorithm to generate chemical isomers of
up to 100 when the number of all chemical isomers exceeds 100.
We can obtain such an algorithm
from the dynamic programming proposed
by Tanaka et al. [25] with a slight modification.
The algorithm first decomposes into a set of acyclic chemical graphs,
next replaces each acyclic chemical graph with another acyclic chemical graph that admits
the same feature vector as that of ,
and finally assembles the resulting acyclic chemical graphs
into a chemical isomer of .
Also, a lower bound
on the total number of all chemical isomers of
can be computed by the algorithm
without generating all of them.
Tables 2,3,4,5,6 show
the computational results of the experiment
in Stage 5 for the five properties,
where we denote the following:
- D-time: the running time (sec.) to execute the dynamic programming algorithm
in Stage 5 to compute a lower bound on the number
of all chemical isomers of
and generate all (or up to 100) chemical isomers ;
- -LB: a lower bound on the number of all chemical isomers of
; and
- : the number of all (or up to 100) chemical isomers of
generated in Stage 5.
From Tables 2,3,4,5,6, we observe that
for many cases
the running time for generating up to 100 target chemical graphs in Stage 5 is less than
0.4 seconds.
For some chemical graph , no chemical isomer was found by our algorithm.
This is because each acyclic chemical graph in the decomposition of has no alternative acyclic chemical graph than the original one.
On the other hand, some chemical graph such as the one in
in Table 2 admits an extremely large number of
chemical isomers .
Remember that we know such a lower bound -LB on the number of chemical isomers
without generating all of them.
6. Conclusions
In this paper, we studied the problem of inferring chemical structures
from desired chemical properties and constraints, based on the framework
proposed and developed in [18, 19, 20].
In the previous applications of
the framework of inferring chemical graphs,
artificial neural network (ANN) and decision tree have been used
for the machine learning of Stage 3.
In this paper, we used linear regression in Stage 3 for the first time
and derived an MILP formulation that simulates the computation process
of linear regression.
We also extended a way of specifying a target value in
a property so that the predicted value
of a target chemical graph is required to belong to
an interval between two specified values and .
Furthermore,
we modified a model of chemical compounds so that
multi-valence chemical elements, cation and anion are treated,
and introduced the rank and the adjacency-configuration of leaf-edges
as new descriptors in a feature vector of a chemical graph.
We implemented the new system of the framework and
conducted computational experiments for Stages 1 to 5.
We found 18 properties for which
linear regression delivers a relatively good prediction function
by using our feature vector based on the two-layered model.
We also observed that an MILP formulation for inferring a chemical graph
in Stage 4 can be solved efficiently over different types of test instances
with complicated topological specifications.
The experimental result suggests that our method
can infer chemical graphs with up to 50 non-hydrogen atoms.
Therefore,
combination of linear regression and integer programming is
a potentially useful approach to computational molecular design.
It is an interesting future work to use
other learning methods such as graph convolution networks,
random forest and an ensemble method to construct a prediction function and
derive the corresponding MILP formulations
in Stages 3 and 4 in the framework.
Author Contributions
Conceptialization, HN and TA; methodology, HN; software, JZ, NAA and KH; validation, JZ, NAA and HN; formal analysis, HN; data resources, KH, LZ, HN and TA; writing—original draft preparation, HN; writing—review and editing, NAA and TA; project administration, HN; funding acquisition, TA. All authors contributed to editorial changes in the manuscript. All authors read and approved the final manuscript.
Ethics Approval and Consent to Participate
Not applicable.
Acknowledgment
Not applicable.
Funding
This research was supported, in part, by Japan Society for the Promotion of Science, Japan, under Grant #18H04113.
Conflict of Interest
The authors declare no conflict of interest. TA is serving as the guest editor of this journal. We declare that TA had no involvement in the peer review of this article and has no access to information regarding its peer review. Full responsibility for the editorial process for this article was delegated to AK and GP.
 Fig. 1.
Fig. 1. Fig. 2.
Fig. 2. Fig. 3.
Fig. 3. Fig. 4.
Fig. 4. Fig. 5.
Fig. 5. Fig. 6.
Fig. 6. Fig. 7.
Fig. 7. Fig. 8.
Fig. 8.







