1 Department of Oncology, University of Alberta, Edmonton, T6G 1Z2, Alberta, Canada
2 Department of Physics, University of Alberta, Edmonton, T6G 2E9, Alberta, Canada
3 DIMEAS, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Torino, TO, Italy
Abstract
This paper presents a historical overview of quantum physics methodology’s development and application to various science fields beyond physics, especially biology and consciousness. Following a successful interpretation of several early 20
Keywords
- Quantum physics
- quantum biology
- quantum metabolism
- consciousness
Quantum mechanics emerged as the most fundamental theory of matter at the turn
of the 19
On the other hand, it is reasonable to expect that evolution, through the process of natural selection over billions of years of experimentation and countless parallel attempts of trial and error, may have solved the decoherence problem so that mesoscopic/macroscopic quantum states are indeed essential features of biological systems. If organized quantum states exist in cells, they are presumably integrated among their components and organelles. This introduces another critical issue into consideration, i.e., that the hierarchical multi-scale organization of living systems must have developed a way of processing information between scales. An efficient means of filtering noise must be present to maintain functional integrity.
Sixty years ago, it was commonplace to suppose that quantum mechanics held the key to the mystery of life. Following on their success in explaining the microscopic properties of non-living matter, the founders of quantum mechanics hoped their theory was powerful enough to explain the peculiarities of the living state of matter, too. Erwin Schrödinger, Niels Bohr, Werner Heisenberg, Eugene Wigner and their contemporaries all offered speculations. At the same time, Schrödinger’s famous book What is Life?, published in 1944 (Schrödinger, 1944), paved the way for molecular biology’s birth in the 1950s. Its major thrust was the author’s attempt to understand biological organization and function achieved with apparent defiance of the second law of thermodynamics, i.e., by reducing the system’s entropy. This paradox can be solved by the inclusion of metabolism, which provides the necessary physical work to overcome the otherwise inevitable increase of entropy. However, what is still very much a mystery is how perfectly synchronized biological processes are across spatial and temporal dimensions connecting the hierarchical organizational scales of a living system. Here, quantum mechanics may indeed come to the rescue, if only we could explain the required absence of decoherence.
Unfortunately, over 50 years, the great expectation that quantum mechanics could easily and powerfully explain living systems and life processes driving them as it had explained other types of matter so exquisitely and precisely has not yet come to fruition. However, parallels between the state of biology today and the state of physics a century ago are striking. Indeed, quantum mechanics is needed to explain the sizes and shapes of molecules and their chemical bonding details. Still, no enunciated “life principle” has emerged from the quantum realm that would single out the living state as in any way a unique form of a physical state. Furthermore, classical ball-and-stick models of protein and other biomolecules and their computational simulations using classical (Newtonian) molecular dynamics methods seem adequate for most molecular, structural, and cell biology explanations. Despite the rapid progress in using classical physics methodology applied to mesoscale systems of relevance to cell biology, there have been persistent claims that quantum mechanics can and should play a fundamental role in biology. For example, biological coherence could emerge through coherent superpositions, tunneling and entanglement. These claims range from plausible ideas like quantum-assisted protein conformational changes (Schempp, 2003) to more speculative suggestions, such as the genetic code having its origin in quantum computation algorithms (Patel, 2001) or quantum-mediated cognitive processing in the brain. Unfortunately, biological systems are so large and complex compared to standard physical systems that it is hard to separate “pure” quantum effects from many essentially classical processes that are also present. There is thus plenty of scope for disagreement about the extent to which life utilizes non-trivial quantum processes. The question also emerges whether biology would be better understood by direct application of quantum physics or by the introduction of quantum-like concepts with their validity limited to living systems.
Why should quantum mechanics be relevant to life, beyond explaining the basic structure and interaction of molecules? One general argument is that quantum effects can facilitate either too slow or impossible processes according to classical physics by harnessing such phenomena as quantum tunneling, superposition, and entanglement, which can yield novel and unexpected phenomena. Given that biology’s basic processes take place at a molecular level, employing quantum effects for greater efficiency does not seem impossible in principle. Quantum coherence, collective modes of excitation, and condensation phenomena represent additional attractive features that could explain the mechanisms behind biological organisms’ manifest stability and integrity.
On the other hand, the Heisenberg uncertainty principle sets a fundamental limit
on all molecular processes’ fidelity. For the cell to perform appropriately, the
right parts must be in the right place at the right time. This appears to be a
much more relevant objective for living systems than the principle of energy
minimization that drives physical processes. Quantum mechanics sets fundamental
limits from the Heisenberg uncertainty principle and impacts the accuracy with
which molecules can cooperate collectively. However, it is reasonable to expect
that some of life’s processes have evolved to the “quantum edge”, where a
compromise may be struck between speed, energy and accuracy. At any rate, the
nineteenth-century view of life as “magic matter”, exemplified by the use of
the terms “organic chemistry” or “life force”, is obsolete today and has been
replaced by a model of the cell as a complex system of highly efficient and
co-ordinated nano-machines operating under the control of genetic software
encoded in DNA and implemented by the cellular transcription/translation
machinery. These tiny components of the cell’s molecular machinery are made
mostly from proteins. They include pumps, motors, rotors, ratchets, scissors,
cables, levers, sensors, and complexes, including protein polymers: actin
filaments, intermediate filaments and microtubules. Their exquisite design,
achieved by two billion years of evolution and natural selection, exhibits
extraordinary efficiency and versatility and represents a challenge to
21
It is abundantly evident that physics and chemistry critically benefitted from quantum mechanics’ conceptual and quantitative power to obtain fundamental insights into the material world. Therefore, it is logical to investigate if biology offers other examples of the application of quantum mechanics. It is currently becoming clear that this may indeed be the case. However, examples of quantum effects in biology can be considered only exceptions rather than the rule (Abbott et al., 2008). Nonetheless, the situation with physical phenomena was not significantly different a hundred years ago. Below, we provide a brief overview of the efforts to apply quantum principles to biology.
The concept of biophotons can be credited to Russian scientist Gurvich (1944), who tried to elucidate the enigmatic processes in embryology using so-called morphogenic fields to be proven correct. Later on, Popp (1988) showed that photons, or quanta of electromagnetic energy radiation, can be both absorbed and emitted by cellular biomolecules such DNA in processes that involve low-intensity ultraviolet ranges of the spectrum. More recently, Albrecht-Buehler (1992) found by innovative experimentation that living cells perceive infrared electromagnetic waves with a peak of their sensitivity close to the wavelength of 1000 nm, in the near-infrared range of the spectrum. He hypothesized that mitochondria, by proton transfer involved in energy production, release photons. Conversely, centrioles, dubbed by him the cell’s eye, are intricately structured to absorb these photons and trigger a signaling cascade. Albrecht-Buehler (1992) has been advocating a theory of cell functioning based on his conviction that the centriole plays a crucial role in orchestrating cellular activities by being both an eye and a cell’s brain. Cell movement is not random but directed and intentional. This is a crucial characteristic that distinguishes living from non-living matter. Cells control the movement of every part of their body.
Furthermore, various parts of the cell can be likened to parts of the human body in their functional roles. The plasma membrane and cortex correspond to the skin and the musculature of a cell, consisting of small autonomously moving ‘microplasts’. Their autonomy implies that cells contain a control system preventing the autonomous units from moving independently and randomly. The bulk cytoplasm, including the mitochondria, organelles and intermediate filaments, comprises the actual cell body excluding the nucleus and corresponding to the ‘guts’ and ‘innards’ of the cell body. Its main cytoskeletal components are the intermediate filaments, although microtubules traverse this compartment everywhere. Microtubules mediate between the control center (the centrosome composed of a pair of centrioles) and the autonomous domains. The control center detects objects and other cells by pulsating near-infrared signals. Cells have structures functioning essentially as their ‘eyes’ in the form of centrioles. They can detect infrared signals and steer the cell movements towards their source. Evidence has been put forward that the signal detection is strongly localized in a narrow band of the near-infrared spectrum. Suppose cells can detect light sources and measure space and time variables such as angles, distances, curvatures or durations. In that case, they must derive these abstract quantities from the physical objects or signals in their environment. In response to exogenous signals, the centrosome may send destabilizing signals along with its radial array of microtubules. The observed destabilization is the signal propagated along the microtubules like action potentials and nerve cells. The destabilization of the microtubules is strictly wavelength-dependent, and its peak area corresponds to the same near-infrared region in which Albrecht-Buehler found cell sensitivity to other objects.
The role of quantum coherence effects in biology was hypothesized by Fröhlich (1968, 1970), who suggested that the modes of vibration of cellular membranes coupled to dipole modes might exhibit the phenomenon of a Bose-Einstein condensate, in which many quanta settle into a single quantum state with long-range coherence. Bose-Einstein condensates are generally associated with very low temperatures. Still, Fröhlich (1968, 1970) hlich proposed that non-linear coupling between a collection of dipole oscillators and phonon modes of lattice vibrations driven by thermal fluctuations from the environment could quite generally channel energy into a single coherent oscillator even at biological temperatures. Fröhlich (1968, 1970) condensates have never been definitively demonstrated experimentally, but recently there has been renewed interest and experimental support, at least for weak condensates. The latter may be crucially important in various chemical kinetics processes taking place in far-from-equilibrium biological nano-systems. Importantly, Fröhlich (1968, 1970) hypothesized that quantum coherence is a property of living cells. Through long-range physical interactions involving dipole-dipole resonances, synchronizing such effects as cell division processes and cell-cell recognition. To date, only scant indirect experimental evidence has been found to support these predictions (Webb et al., 1977; Keilmann and Grundler, 1984). A recently published report implicated Fröhlich’s condensation in the absorption and redistribution of THz electromagnetic energy in proteins (Lundholm et al., 2015).
Another example of quantum tunneling with biological relevance concerns the chemistry of proteins. Vaziri and Plenio (2010) described the action of ion channels using quantum tunneling. Some proteins contain active sites that bond to hydrogen, and to reach the sites, the hydrogen atom has to negotiate an elaborate and shifting potential energy landscape. Quantum tunneling can speed up this process. Studying just how important tunneling might be is highly challenging because many complicated interactions occur as the protein molecule jiggles around and changes shape due to thermal agitation. Vattay et al. (2015) suggested that life has evolved via protein behavior at the edge of quantum criticality. Recent results using deuterium by Klinman and Kohen (2013) seem to confirm that quantum tunneling is indeed significant, and they raise the fascinating question of whether some proteins have evolved to take advantage of this, making them in effect “tunneling enhancers” (Kohen and Klinman, 1998). If true, this could pave the way to understand how quantum effects can be amplified from molecular to cellular scales. Even a small advantage in speed or accuracy can bootstrap into overwhelming success in evolution because natural selection exponentiates the relative proportion of the winners over many generations. Mutations are the driver of evolution, so in this limited sense, quantum mechanics is a certainly contributory factor to evolutionary change, e.g., in environmentally-stressed bacteria (McFadden, 2000), which could boost their survivability.
An important study of photosynthesis by Engel et al. (2007) was a game-changer in quantum biology’s emerging field. Photosynthesis is a highly complicated and sophisticated mechanism that harvests light energy to split water using individual photons to create a cascade of reactions. The process is extraordinarily efficient and represents a classic example of how evolution has fine-tuned a physical system’s design to attain near-optimal performance. Recently, photosynthesis’s quantum mechanical nature has been demonstrated theoretically and experimentally by several research groups (Arndt et al., 2009; Collini and Scholes, 2009; Collini et al., 2010). The light energy’s primary receptor is a complex of pigment molecules known as chromophores that can become excited and pass on this dipolar excitation’s energy in a multi-stage process to the final reaction center where charge separation occurs. Because the photon’s wavelength is much larger than the molecular assemblage, a superposition state of many exciting pigment molecules is initially created and proceeds to evolve over a timescale of some hundreds of femtoseconds. Engel et al. (2007) used laser excitation and probe pulses to study these light-harvesting complexes’ relaxation pathways and observed a “quantum beating” effect. The maximum amplitude of the excitation visits and revisits different molecules in the system coherently. They claim that, with appropriate timing, the system can “grab” the coherent excitation (which persists for a few hundred femtoseconds) with greater probability than if it was merely distributed according to classical statistical mechanics, and this could lead to a many-fold increase in the speed of energy transfer. Their results have subsequently been augmented by Collini and Scholes (2009), who demonstrated room temperature coherence in electron excitation transfer processes along polymer chains. An important feature of photosynthesis is that the molecular architecture involved is structured in a highly unusual and compact manner, suggesting it has been “custom-tailored” to exploit long-range quantum effects. The particular configuration may be efficient at preserving coherence for surprisingly long durations, enabling the system to “explore” many pathways simultaneously and thus speed up a “solution” (i.e., delivering energy to the reaction center). In the light-sensitive complexes, reaction centers capture individual photons and transfer exciton energy by tunneling, avoiding decoherence even at room temperatures, which has been invoked on numerous occasions as a severe impediment to quantum biology in general (Tegmark, 2000) but also defended on various grounds (Hagan et al., 2002) as discussed below.
Ritz et al. (2000) have advocated using quantum mechanics by purple bacteria and light-harvesting in carotenoids. They demonstrated the feasibility of quantum effects using high-performance computing at the atomic level of simulation for the relevant enzymatic reactions. It should be mentioned that the use of quantum mechanics to explain photosynthesis can be viewed as a natural progression of theory development, which was preceded by extensive experimental (Möbius and Kuhn, 1988) and theoretical (Tuszyński et al., 1999) work on the so-called Scheibe aggregates. Scheibe aggregates are thin films composed of chromophore molecules that have been engineered to harvest light energy and funnel exciton quanta at specific sites through quantum hopping and funneling. Another example of quantum tunneling with biological relevance concerns the chemistry of proteins, which spontaneously fold into complex three-dimensional shapes, i.e., their tertiary structures. The protein folding problem has not been solved yet, and it can be indeed unsolvable within the methodology of classical physics. However, quantum search algorithms can provide a sufficiently quick way of finding a three-dimensional protein structure for an initially outstretched polypeptide chain.
Since the discovery of potassium K
Beck and Eccles (1992, 2003) investigated the neurotransmitter release process occurring in the neuronal synapses and proposed that it is subject to the Heisenberg uncertainty principle. They further suggested that this process involves quantum mechanical tunneling. They also stated that quantum indeterminacy into neurotransmitter release mechanisms would provide a means for the emergence of the human free will of action. In particular, a quantum process involved in this mechanism, such as an electron tunneling through a potential energy barrier, could trigger exocytosis. While this is a desirable possibility, the vesicle’s physical size and many neurotransmitter molecules encapsulated in it appear to make it very improbable that this could lend itself to quantum tunneling. In conclusion, while the Beck-Eccles model contains very attractive ideas, the theory’s main assumptions are not easily reconcilable with modern views of the molecular biology of vesicular neurotransmitter release (Smith, 2009).
Lowenstein (2013), in a most exciting book, made argued convincingly in favor of the usefulness of quantum mechanical processes in receptor functions, which could facilitate molecular recognition. Since sensory inputs depend on molecular recognition between ligands and receptors (in molecular processes underlying such physiological functions as olfaction, vision, sound, touch), they all involve single molecules behaving as triggers for amplifying these signals at the neuron level and leading to an eventual brain-level activation. This amplification mechanism involving quantum signaling connects the microscopic and macroscopic levels, critical to our understanding of the so-called binding problem in human cognition and consciousness.
Gauger et al. (2011) have recently demonstrated that bird navigation is based on quantum entanglement that persists for at least 20 µs, which is longer than the currently maintained laboratory experiments at comparable temperatures. It is well-known that some birds perform amazing navigation feats using various cues that include the local direction of the Earth’s magnetic field. The nature of the magnetic sensor has, however, remained something of a mystery. How is the angle of the field relative to the bird translated into neural information? The problem is particularly acute because the magnetic field penetrates the entire organism. Still, in the case of the European robin, at least a plausible case has been made that the key lies with a class of proteins found in the bird’s retinas. In effect, the robin actually “sees” the magnetic field. The mechanism being studied by Ritz (2011) and Ritz et al. (2009) appeals to photo-activation above the thermal noise of a two-dimensional array of aligned proteins, producing radical ion pairs involving singlet two-electron states. So long as electrons in an entangled state experience identical magnetic environments and quantum coherence is preserved, the spins precess in synchrony. However, in addition to the Earth’s ambient field, nuclear magnetic fields present hyperfine splitting. If one of the electrons in a singlet pair moves away, the combined nuclear and terrestrial magnetic field it experiences will change, causing the singlet state to oscillate with a triplet state with a periodicity depending in part on the strength and relative orientation of the Earth’s field. The system may then de-excite in stages and initiate a reaction that acts as a chemical compass because the relative proportion of the reaction products can depend on the singlet-triplet oscillation frequency.
McFadden (2002) maintains that biological evolution, such as present in bacterial mutations under toxic stress, must involve quantum computing to explain its efficiency, including anticipatory steps. Another early and recurring speculation is that some biological mutations come about as a result of quantum tunneling. The genetic basis of life is written in the four-letter alphabet of nucleotides A, G, C, and T that pair together to make up the rungs of the helical ladder structure of DNA. The normal assignment is that T pairs with A and G pairs with C are held together by two or three hydrogen bonds, respectively. According to a proton’s position, the nucleotide bases can exist in alternative chemically related forms, known as tautomers. Quantum mechanics predicts a finite probability for the proton to tunnel through the potential barrier separating these two states, leading to mispairing, for example, of T with G instead of A. Mutations are the driver of evolution, so in this limited sense, quantum mechanics could become a certainly contributory factor to evolutionary change. McFadden (2000, 2002) has built on this process to suggest a quantum model of adaptive change, in which environmentally stressed bacteria seem able to select favorable mutations that boost their survivability. Even for a medium-sized protein, the number of possible amino acid mutations is astronomical. Over the biological scale of evolution on Earth, there could be no possibility of attempting all of these mutations to select favorable ones. Therefore, a quantum search algorithm could once again come to the rescue and solve an otherwise unsolvable problem.
Experimental data show that signaling and ionic conductivity in cells via microtubules (MTs) may offer real potential for both classical and quantum information processing at a subcellular level. However, there are numerous arguments in the literature both for and against the role of quantum effects in MTs. Theoretical and computational models investigated the conditions for quantum processing of information in microtubules and microtubule assemblies. For example, Craddock et al. (2009) used an approach based on cellular automata and investigated classical and quantum neighbor interaction rules. With a characteristic MT geometry and a tubulin dimer neighborhood in a hexagonal configuration, the interior of tubulin was represented electrostatically, showing two nanoscale regions with a positive electric charge separated by a negative potential region forming a double-well potential. The position of a mobile electron oscillating within this double potential well was the critical factor for the state of individual tubulin. It resulted in transitions between two local energy minima found from conditions for minimizing the system’s energy associated with electrostatic interactions between the neighboring electrons and exposed to thermal fluctuations of the environment. This model’s classical version allows only transitions for electrons with sufficiently high energy to overcome the potential barrier (approx. 100-150 meV). The new configuration lowers the system’s energy.
Conversely, if the new configuration raises the system’s energy, the transition
occurs with a probability proportional to the Boltzmann factor, namely
exp(-
Speaking of clocking mechanisms, metabolism at a cellular level appears to provide the most fundamental life rhythm. Demetrius (2003) proposed a more general theory called quantum metabolism, discussed in more detail below, which states that metabolic energy is universally generated by all living systems using quantum mechanics principles. It involves collective quantum oscillations of metabolic enzymes, which we discuss separately below.
Turning to possible quantum biology effects occurring in organs and tissues of the human body, it has been shown that the human eye can detect light at an extremely low threshold, with as few as 2-3 photons being detected at a time (Hecht et al., 1942). Similarly, the seminal work of Turin (1996) and Brookes et al. (2007) has provided strong arguments to the claim that the sense of smell (olfaction) is based on a quantum resonant energy transfer mechanism involving vibrational degrees of freedom of aromatic molecules and receptors in the membranes of olfactory nerves.
Although the preceding examples have been in the literature for some years, they have not led to a widespread acceptance that quantum physics is essential for biology. The main reason for this skepticism is the problem with decoherence mentioned above but requires a closer analysis.
While the examples listed above provide a case for quantum mechanics playing a biological role, they all confront a profound and fundamental problem. Effects such as coherence, entanglement and superposition can be maintained only if the quantum system avoids decoherence caused by interactions with its environment. In the presence of environmental noise, the delicate phase relationships that characterize quantum effects get scrambled, turning pure quantum states into irregular mixtures and marking a transition from quantum to classical behavior. Only if decoherence can be kept at a sufficiently low level will explicitly quantum effects be allowed to persist. Therefore, quantum biology claims stand or fall on the precise determination of the decoherence time scale. If decoherence happens too fast, the system will equally rapidly find itself in the classical regime before any biochemical or biological effects of interest happen.
In recent years, much attention has been given to decoherence, and its avoidance, by physicists working in quantum computation and quantum information science. A quantum computer can process information more efficiently using quantum states to perform logical operations through quantum superpositions’ coherent evolution. Decoherence represents a source of computational error, so the idea is to design architectures that minimize the impact of decoherence. A key parameter is a temperature: the higher the temperature is, the stronger the decoherence. For this reason, most attempts at quantum computation employ ultra-low temperature environments such as superconductors or cold atom traps.
At first glance, a living cell’s warm and wet interior seems a very unpromising
environment for low decoherence and long-range coherence. Approximate
calculations suggest decoherence times on the order of 10
There are two other ways decoherence could be diminished for long enough to
enable biologically important processes to occur. The first is screening: if the
system of interest can be quasi-isolated from the decohering environment,
decoherence rates can be sharply reduced. According to Matsuno (1999) and Matsuno and Paton (2000), organisms may exploit thermodynamic gradients by
acting as heat engines, thereby drastically reducing certain molecular complexes’
effective temperature. An example of this situation is the slow release of energy
from ATP molecules at actomyosin complexes, which implies an effective
temperature for the actomyosin of a mere 1.6
The second possibility involves decoherence-free subspaces. As part of the effort to build a quantum computer, much attention has been given to identifying Hilbert space subspaces unaffected by the system’s coupling to its environment. Paradoxically, when a system couples very strongly to its environment through certain degrees of freedom, it can effectively “freeze” other degrees of freedom by the quantum Zeno effect, enabling coherent superpositions and even entanglement to persist. A relevant example is that of a double-well one-dimensional potential Hamiltonian. A particle placed in the lowest energy state of one well will tunnel back and forth through the intervening barrier, oscillating with a specific frequency. If the particle is placed instead in an excited state of the well, this flip-flop frequency will differ. Thus, an initial state consisting of a superposition of lowest energy and excited states will soon evolve into a complicated combination as the flip-flops get out of phase. However, suppose the particle is allowed to interact strongly with an external heat bath. In that case, the environment will have the effect of forcing the disparate oscillations into synchrony (entrainment), maintaining some amount of quantum coherence paradoxically because not despite environmental interactions.
The critical assumption that quantum coherence is eliminated by increased temperature is no longer assured when non-equilibrium states and non-linear interactions are included. For example, this is the case with laser action, and possibly laser-like coherent pumping hypothesized to take place in biological cells and, in particular, with periodic lattice structures such as microtubules or actin filaments. Recent experimental evidence demonstrates that quantum spin-transfer processes between quantum dots can be more efficient at room temperature than at or near absolute zero (Ouyang and Awschalom, 2003). The critical factor in these processes is that the temperature-enhanced quantum interaction involves benzene rings, which are organic molecules having delocalized electron charge density. Another set of experiments has shown that quantum waves are generated by biological porphyrin molecules (Hackermüller et al., 2003). These molecules are found in heme groups of the red blood cells, for example.
By analogy, in living cells, delocalized electrons in aromatic amino acids, for example, may allow proteins to harness thermal environmental energy to promote, rather than destroy, quantum states. Quantum interactions among tryptophans in hydrophobic pockets (nonpolar, water excluding intra-protein regions) govern protein folding (Klein-Seetharaman, 2002), and similar effects appear to mediate potassium channel function (Jiang et al., 2003).
Finally, in this connection, special attention must be paid to the hierarchical structural organization of biological systems, which in turn translates into an interlocking hierarchy of time scales. Faster time scales may inform processes at slower time scales about much faster processes associated with a small spatial level. For example, the neurotransmitter systems undergo changes synchronized with endogenous circadian rhythms and fluctuate in accordance with the seasons of the year. This results in a vast range of time scales over 8 to 10 orders of magnitude along the time axis. Because neuronal processes at the millisecond time scale readily affect neural states at the circadian level, it can be argued that picosecond-scale quantum states can affect millisecond-scale neural activity. Therefore, a postulated requirement that MT information processing must involve long-lived coherent states with lifetimes at or above a millisecond time may not condition sine qua non for it to affect neural events. However, multiple oscillators must stay interdependent and sensitive to redundant patterns. Such interdependence allows processes operating at the shortest time scales where quantum mechanisms dominate to affect more extended time-scale events and broader size-scale processes. Here again, the coupling between spatiotemporal scales and amplification of quantum effects may offer a solution to some of these problematic issues.
While quantum mechanics was developed with elementary particles in mind, its subsequent applications extended its validity to systems of many particles such as those encountered in condensed matter physics, e.g., describing the conduction electron “sea”, excitons, magnons, polarons, polaritons, etc. These types of quantum properties of macroscopic physical systems are called collective excitations. Many particles under specific conditions cannot be separated into individual wave functions for each particle; instead, the system is described by a single wave function describing its collective behavior. This physical property is called quantum coherence, and it is characterized by individual particles losing their separate identities such that the entire system acts as a whole. Particles that were once unified in a shared quantum state remain physically connected even at a distance. Measurements made on one particle cause the collapse of the entire wave function for the system, resulting in an instantaneous effect for all particles, no matter where they are spatially located. This intrinsically quantum-mechanical interaction over distance is referred to as non-local quantum entanglement. Decoherence occurs when such a system interacts with its environment in an irreversible thermodynamic manner, causing different particles engaged in a quantum superposition state to no longer interfere with one another. Decoherence plays an important role in the criticisms leveled at quantum mechanics to describe macroscopic systems, especially biological ones, as we discuss later.
In this section, we have drawn on the lessons learned from the quantum theory of
solids. An adequate mathematical representation of solids (e.g., crystals or
semiconductors) leads to energy
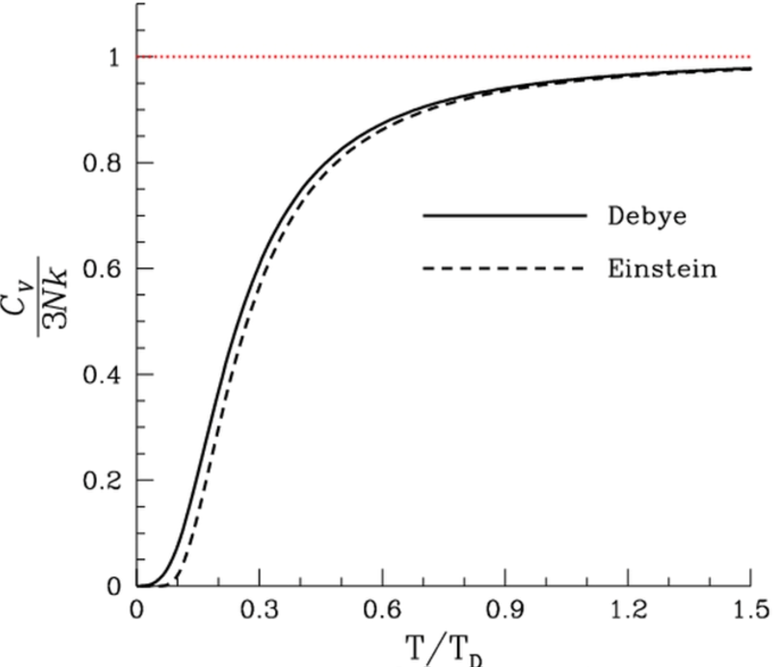 Fig. 1.
Fig. 1.A characteristic plot of the specific heat of solids as a function of temperature based on https://en.wikipedia.org/wiki/Debye_model where discussion can be found about the comparison between the Debye model of a solid and the Einstein model. In contrast to the Debye model’s correct assumptions, the Einstein model considered lattice nodes as oscillating independently around their equilibrium positions.
It can be shown that the quantum nature of solids manifests itself at
temperatures up to the characteristic value (T
The specific heat of solids satisfies an empirical relationship, expressed by the Dulong and Petit law, which states that above a characteristic temperature (Debye temperature), the specific heat of solid increases in proportion in the high-temperature regime to 3NkT. At low temperatures, the relationship between specific heat and temperature is a cubic dependence on absolute temperature. As developed by Debye, the quantum theory of solids was proposed to explain these empirical relations. The crucial observation in these models was the heat capacity’s consideration as associated with the propagation of vibrations of atoms (phonons) in a crystalline solid, not individual atomic oscillations as proposed by Einstein.
However, temperature as an independent variable is not relevant to live organisms, which are essentially isothermal. Energy flow in living organisms is mediated by differences in the turnover time of various metabolic processes in the cell, which occur cyclically. Empirical studies that go as far back as Lavoisier’s work but mainly to the studies done by Kleiber (1961) demonstrate that metabolic processes are characterized by cycle times, which are related to the metabolic rate. Basal metabolic rate is defined as the rate at which the organism transforms the free energy of nutrient molecules into the body’s metabolic work, including maintaining its physiological temperature. The recently proposed theory of Quantum Metabolism (Demetrius, 2003; Demetrius and Tuszynski, 2010) has employed the methodology of the quantum theory of solids developed by Einstein and Debye to provide a molecular-level explanation of these empirical relations called allometric scaling laws.
Debye (see Ashcroft and Mermin, 1995) made a significant advance in
condensed matter physics by considering the heat capacity as associated with
harmonic vibrations of atoms in a crystalline solid. The vibrations were assumed
to propagate within the solid due to the interactions between the neighboring
atoms. They were then treated according to quantum theory and satisfied with the
following quantization condition. The energy stored by an oscillator with
frequency
ATP’s production, the energy currency of living organisms, is mediated by the
coupling of two molecular chains: (a) The redox chain, which describes the
transfer of electrons between redox centers within the electron-transport chain.
(b) The ATPase motor, which is involved in the phosphorylation of ADP to ATP.
There are two distinct mechanisms by which these two events are coupled:
oxidative phosphorylation, which involves an electrical process, and substrate
phosphorylation, which implicates a purely chemical process. This cyclic
process’s transit time determines the total metabolic flux, i.e., the number of
proton charges released by the redox reactions. This transit time, or the
metabolic cycle time, denoted
The molecular dynamics model proposed to investigate this coupling by electrical
and chemical means assumes that the energy generated by the redox reactions can
be stored in terms of coherent vibrational modes of enzymatic oscillators
embedded in the cellular organelles. Quantum Metabolism rests on the notion that
the enzymatic oscillations in cellular organelles and the material oscillators in
crystalline solids can be analyzed using essentially the same mathematical
formalism used by Debye in the quantum theory of solids. This realization is
deduced from a formal correspondence between the thermodynamic variables in
physical systems and biological processes’ metabolic quantities. The principal
variables in the quantum theory of solids are the specific heat, the
Gibbs-Boltzmann entropy and the absolute temperature T. The fundamental
unit of energy is given by E = k
On the other hand, the critical variables in the theory of quantum metabolism
are the metabolic rate, the entropy production rate and the mean cycle time,
Demetrius (2003) introduced the term enzymatic oscillator since enzymes undergo electrochemical oscillations about their fixed positions. These oscillations are generated by the metabolic energy associated with electrons’ transfer between donor and acceptor pairs in the mitochondria’s electron transfer chain. Since their power spectrum exhibits an exponent vastly different from that for random behavior, a description of the metabolic activity involving mitochondrial proteins involves coupled quantum oscillators of the Debye type.
Quantization of metabolic energy is due to integer ATP numbers being produced in
the cell’s mitochondria and their relatively low energy content comparable to
physical quantum processes. The almost universal energy currency in biological
systems is the ATP molecule. ATP synthesis in a mitochondrion or a chloroplast
requires approximately 60 kJ/mol of energy delivered through electron
transport reactions or absorption of photons, respectively. ATP hydrolysis
releases 30.5 kJ/mol of free energy (
Integrating this development of quantum effects in biology into a broader quantum science framework, we can delineate two distinct thought lines. First, quantum phenomena and theories dealing with individual particle interactions. This approach goes back to the photoelectric effect and the Compton scattering effect, where a photon interacts with an electron demonstrating the particle aspect of electromagnetic radiation in the first case and wave nature of an electron in the latter. Most of the so-called “quantum weirdness” can be ascribed to binary interactions between individual microscopic entities with properties such as entanglement, long-range correlations, delocalization, tunneling, etc., providing striking examples of how quantum physics differs from the classical paradigm. The current focus within the emerging field of quantum biology on photosynthesis parallels early quantum physics development through individual particle experiments, especially the role of the photoelectric effect.
On the other hand, the first experiment correctly interpreted using the quantization principle, namely the black body radiation and Planck’s energy quantization formula (Planck, 1959), to speak to a different group of quantum phenomena theoretical building blocks of quantum theory, i.e., quantum statistical mechanics. Applications of quantum statistics dominated quantum theory in several fields, particularly condensed matter physics (Ashcroft and Mermin, 1995). This approach gave rise to the explanations of specific heats of solids first by Einstein, then by Debye, and the development of quantum theories of magnetism, semiconductivity, and other collective quantum effects. It is worth mentioning that within condensed matter physics, one finds examples of macroscopic quantum phenomena countering the objections voiced by some that quantum theory is limited to the microscopic world. Both superconductivity and superfluidity exhibit “quantum weirdness” at a macroscopic scale, although they still require extremely low temperatures to be sustained. However, magnetism is an inherently quantum state of matter that could not arise without spin, a quantum variable, and it exists at both macroscopic scales and high temperatures. Laser action is an example of a macroscopic quantum coherent state at high temperatures. Due to a non-equilibrium condition created by external energy pumping, Fröhlich claimed to provide a blueprint for a fundamental explanation of the living state of biological matter. Quantum metabolism is a theory that closely parallels the Debye theory of the specific heat of solids in the realm of quantum statistical properties of living systems.
Table 1 provides a general overview of the areas of science where quantum physics found applications, both in equilibrium and non-equilibrium situations (A) refers to quantum science’s totality as is known today, (B) includes equilibrium quantum phenomena that include individual particles and their statistical ensembles, (C) encompasses nonequilibrium quantum phenomena in physics and biology. Since living systems are out of thermodynamic equilibrium, in principle, all quantum mechanics’ biological applications should be considered nonequilibrium quantum phenomena. An extension of these phenomena to the realm of neuroscience is a vast and hugely challenging endeavor that may require many decades to complete. In the sections that follow, we discuss these challenges and our current understanding of quantum models of consciousness.
| A. QUANTUM SCIENCE | |||
| PHYSICS, CHEMISTRY, BIOLOGY | |||
| B. EQUILIBRIUM QUANTUM PHENOMENA | |||
| QUANTUM MECHANICS | QUANTUM STATISTICS | ||
| INDIVIDUAL PARTICLE REPRESENTATION | STATISTICAL ENSEMBLE | ||
| FEW PARTICLES | MANY PARTICLES | ||
| PHYSICAL | BIOLOGICAL | PHYSICAL | BIOLOGICAL |
| Photoelectric effect | Photosynthesis | Einstein/Debye solids | Quantum metabolism |
| C. NONEQUILIBRIUM QUANTUM PHENOMENA | |||
| PHYSICAL | BIOLOGICAL | ||
| Laser action | Fröhlich coherence | ||
Does the study of consciousness belong in natural sciences, or is it a philosophical or even metaphysical inquiry area? These questions have been pondered by many scientists, philosophers and spiritual leaders whose opinions diverge mainly due to the subjective nature of consciousness. The existence of this phenomenon cannot be denied, as we all experience it as sentient humans. The author of this paper firmly subscribes to the assertion that not only is the study of consciousness a valid area of scientific research but, indeed, one of the most fundamental unsolved scientific problems of the modern age. The enigma of consciousness has challenged all conventional theories. The brain is considered an information processing device similar to a classical computer, with neurons and synapses playing the roles of bit states storage devices and logical gates, respectively. Specifically, the following unresolved issues await elucidation: 1) the so-called “hard problem” related to the nature of conscious experience, i.e., “qualia”, 2) the binding problem, i.e., how disparate brain processes can be unified into a sense of “self”, 3) the mechanism of the transition from pre-conscious processes to consciousness itself, 4) the existence, limitations and manifestations of free will, or non-algorithmic (e.g., intuitive) processes, 5) subjective perception of the flow of time, 6) nonlocality, i.e., paranormal connections between humans and also between humans and other-than-human species cross large spatial and temporal domains (e.g., precognition, telepathy, etc.).
Most conventional neuronal-level computational approaches suggest conscious experience “emerges” at a critical level of computational complexity. Binding is proposed to involve temporal synchronization (e.g., via coherent 40 Hz oscillations). However, it is clear that with no sense of conscious experience, temporal synchronization amounts simply to a correlative epiphenomenon and not an explanatory mechanism. On a positive note, potentially the easiest to tackle is the problem involving the transition from pre-conscious processes to full consciousness. It is currently almost universally agreed upon that most of the brain processes are non-conscious. Hence, consciousness constitutes the “tip of an iceberg” of the totality of brain activities. However, no specific region of the brain can be identified as housing consciousness; neural activity in a given area may be non-conscious at one moment and be involved with consciousness at another.
Inspired by applying quantum theoretical methods to studying the brain and other biological structures, scientists began to investigate brain functioning from the microscopic quantum physics level. One of the first attempts to describe the brain, especially the concept of memory as a broken symmetry state, using quantum physics terminology was made by Ricciardi and Umezawa (1967). Based on experimental observations of brain activity, they proposed that the brain could be understood as a spatially- distributed system placed into specific quantum states by external environmental stimuli. Thus, information can be thought of as being coded into the brain in the form of metastable excited quantum states, representing short-term memory. This type of memory code could then be transferred more permanently to the system as a condensation transition to the ground state, similarly to the Bose-Einstein condensation effect in superfluids and other exotic physical systems. The process was envisaged as explaining learning and long-term memory. This Ricciardi-Umezawa model views the brain as representing a biological equivalent of spontaneous symmetry breaking in the brain’s dynamics (Stuart et al., 1978). It relates macroscopic quantum states with long-range correlations to memory specifically, and it was later extended to mixed physical states whereby the brain is considered to consist of two separate interacting parts. The first part involves classical electrochemical interactions of the brain’s neurons, while the second generates and sustains a macroscopic quantum state responsible for creating and maintaining memory. Extensions of these early quantum field theory models to higher dimensions, networks and non-equilibrium situations have been recently proposed (Nishiyama et al., 2020).
Subsequently, a major effort has been placed on the mechanistic explanations of the role of the material substrate for conscious processes, namely protein polymers and their networks located within individual cells and referred to collectively as the cytoskeleton, especially the microtubules and their axonal and dendritic bundles (Hameroff, 1987, 1998). Penrose (1989, 1994) investigated the relationship between consciousness and modern physics in a fascinating exposition of Turing machines, Gödel’s theorem, chaos, classical and quantum mechanics, thermodynamics, relativity, cosmology, quantum gravity, quasi-crystals, and brain neurophysiology. Penrose strongly argued that quantum effects play a fundamental role in understanding human consciousness by enabling the brain to perform non-computable operations related to cognitive functions. In his work, Penrose argued that a new type of physics is required to explain the mind’s workings and the fundamental nature of consciousness. Consequently, he examined the distinctions between classical and quantum physics, focusing closely on the measurement problem, and relating the collapse of the quantum wave function to conscious events. In this latter aspect, he drew on the so-called Objective Reduction phenomenon, which causes a gravitationally-induced wave function collapse. This has subsequently led to the hypothesis about a concrete realization of this process, jointly formulated by Hameroff and Penrose (2014). They predicted that microtubules within neurons provide the brain with the requisite structures, which can orchestrate the wave function’s collapse via quantum computations if sufficiently abundant and strongly correlated. This combination has become known as the Penrose-Hameroff Orchestrated Objective Reduction (Orch OR) theory.
The Orch OR theory’s main idea rests on is that microtubules within the brain’s neurons function as quantum information processors at physiological temperature. They are composed of microtubule protein subunits (“tubulin dimers”), which transiently occupy quantum superposition states involving two or more conformational (or electronic) states (i.e., quintessential quantum bits, or “qubits”). Orch OR further asserts that tubulin-based qubits, when in a quantum superposition, interact/compute with other superpositions of qubits localized in tubulins arrayed over microtubule lattices. These interactions involve nonlocal quantum entanglements, eventually reducing (“collapsing”) to particular classical tubulin states after approximately 25 ms (which corresponds to the frequency of 40 Hz mentioned above). This type of quantum state reduction could be interpreted as yielding conscious perceptions and volitional choices, which then when transmitted to the next level of organization, would control neuronal actions. This idea is very similar to that on which technological quantum computing is based, with the exception that Orch OR proposes the representation of qubits to involve tubulin protein conformations (Hameroff et al., 2014) and that the reduction/collapse events occur as a result of a specific objective threshold (objective reduction) rather than environmental interaction controlling the process.
Therefore, the Orch OR theory regards a conscious event to represent a quantum computation process, which concludes with objective state reduction representing a realized thought. The brain’s biological conditions, including synaptic activity, influence the quantum computations, thus orchestrating the qubits’ collapse and giving rise to a conscious event at a specific moment in time. The Orch OR theory’s central postulate can be stated as placing consciousness within the brain’s microtubules, which operate at the interface between classical neurophysiology and quantum mechanical forces. These are very bold claims that have found both ardent supporters and vocal critics in the scientific community. However, the enduring power of attraction of Orch OR for a solid base of support across science, philosophy and beyond is a testament to the creative influence of this work on the field of scholarly inquiry. It should also be stated that there appears to be no competing theory at this level of microscopic abstraction. Moreover, Orch OR is experimentally testable, although no tests have been performed yet.
The main issues the critics of Orch OR have identified can be broadly grouped into the following three questions:
1) Experimental evidence, which would link the activity of a single synapse with the dynamics of neural assemblies, is still lacking. Hence, the relevance of quantum processes to cognitive processes remains a claim requiring clear experimental validation.
2) To date, there seem to be no specific and compelling quantum mechanical properties needed to explain psychological and neurological phenomena. The relevance of quantum effects on the brain’s structure and function does not necessitate their involvement in explaining consciousness, although this point can be argued because of the “hard problem” (Smith, 2009).
3) Biological structures of relevance to Orch OR, such as microtubules and neurons, are relatively large and function at high temperatures in non-equilibrium systems, hence they do not neatly fit into the class of quantum mechanical systems from the quantum physics point of view. As such, it appears that it is next to impossible for them to remain in states of linear superposition capable of coherently interfering with one another. Thus, at first sight, thermal and environmental decoherence would eliminate any possibility of quantum effects playing a role in brain processes. This point is still an open issue.
Additionally, specific representations of Orch OR to date have side-stepped quantum chemistry, which appears to be an important link between quantum physics and quantum biology. This needs to be revisited. Shielding of quantum effects in neuronal microtubules has been used to explain the lack of decoherence but without validation of this claim by controlled experiments. Finally, the involvement of quantum gravity’s role in spacetime geometry as opposed to causing decoherence is a major claim that so far has been outside of the scope of experimental techniques available today. However, recent reports (Donadi et al., 2020) have shown that quantum gravity can only play a role in quantum collapse for large enough systems.
Concerning empirical validation of quantum hypotheses about consciousness, there have been no serious attempts to validate any of these claims until now. However, recent advances in nanotechnology allow the initiation of precise studies into the biophysical workings of sub-cellular structures such as microtubules, actin filaments and mitochondria. With this in mind, the present lack of evidence supporting quantum brain theories such as Orch OR should not be regarded as proof of their incorrectness. Instead, we should consider this research area as requiring intense scientific investigations using the most up-to-date experimental and computational tools. Note also that most of the enigmatic features of consciousness are still unexplainable using classical neuroscience.
On the other hand, quantum theories seem to provide a means to address these questions and a methodology for new and more fruitful investigations into consciousness. It is particularly significant to mention here that macroscopic quantum phenomena such as superconductivity, superfluidity, magnetism, and laser action exist at relatively high temperatures (although they sometimes require very finely tuned parameters) and that these phenomena cannot be explained using classical physics but necessitate the use of macroscopic quantum coherence within a condensate. By extension, not all phenomena observed in macroscopic systems can be expected to behave classically. Hence, while the first two arguments against quantum consciousness could be viewed as representing a general resistance to the idea of quantum consciousness, the third is an argument that warrants serious concern. Further, macroscopic quantum phenomena such as superconductivity and superfluidity require a high degree of environmental isolation to avoid decoherence.
Consequently, for such phenomena to emerge and exist in the brain, Nature would have to have discovered mechanisms that isolate the active system against environmental decoherence. On the other hand, ferromagnetism requires no such isolation, only a sufficiently low temperature below the Curie temperature value. The subject of decoherence in quantum computation in microtubules has been particularly vigorously discussed in the literature, with strong arguments for and against the discussions.
Specifically, Tegmark (2000) made a strong objection to the Orch OR theory
and the notion of quantum brain dynamics in general. He based his arguments on
calculations of neural decoherence rates for regular neuron firings and kink-like
polarization excitations in microtubules within neurons. Tegmark stated that the
degrees of freedom in the human brain must be considered classical and not
quantum due to the major gap in the time scales involved. The thermal decoherence
time-scales he computed for superpositions of solitons moving along a single
microtubule are approximately 10
Moreover, Hagan et al. (2002) discussed various mitigating factors such as
the effects of screen thermal fluctuations, for example, the layers of ordered
water, ions, and gel states surrounding microtubules in neurons. Recalculating
the effects using corrections for the parameter values, Hagan et al. (2002)
found new decoherence rates in the range 10
As mentioned above, various meticulously conducted experiments clearly showed room-temperature quantum effects in photosynthetic systems (Engel et al., 2007) and conjugated polymer chains (Collini et al., 2010). Moreover, nonthermal radiation at a frequency of 8.085 MHz was observed being emitted from MTs. While this is not necessarily an indication of quantum condensation or coherence, it remains a distinct possibility (Pokorný, 1999). Reimers et al. (2009) and McKemmish et al. (2009) stated in their critical assessment of quantum states in microtubules that this radiation could simply result from a weak condensate being formed but not from any form of coherence required by the Penrose-Hameroff model. These results, however, are based on a linear chain of coupled oscillators in contrast to the cylindrical geometry of MTs, leaving the question still open. Another issue worthy of serious consideration is the wide range of dynamical behavior expected to occur in tubulin dimers when they are polymerized into MTs. This casts doubt on the claim that intact MTs allow two potential conformations of tubulin dimers.
Nonetheless, McKemmish et al. (2009) demonstrated that repeated exchanges
between the GTP and GTP-bound forms of tubulin within MTs are not supported by
current experimental evidence. While the conformational states are generally
identified as tubulin-GTP and tubulin-GDP, the Penrose-Hameroff model does not
specify the precise nature of the conformational states envisaged, so
alternatives remain a possibility. These alternatives could involve charge
transfer mechanisms, electronic transitions to excited states, and exciton-phonon
coupling mechanisms. Notably, there is evidence for conformational changes (i.e.,
tilting to one or the other side) for
In terms of molecular biophysics, based on their ability to propagate signals through the neuron, MTs and actin filaments can be viewed as computationally relevant nanowire networks that operate within neurons (Woolf et al., 2010). Rather than inputs to neurons being limited to causing discrete responses, this viewpoint offers the possibility of local and global neuroplasticity, based on the cytoskeleton computing and storing templates that translate patterns of inputs across widespread synapses into the “behavioral” output of the neuron. This behavioral output of the neuron is not limited to axonal firing and dendritic integration of electrochemically-mediated inputs. Instead, it includes connecting the cell nucleus with the postsynaptic density, initiating transport of receptor molecules, membrane proteins, organelles, and mRNA, regulating neurite motility, restructuring of spines and complex dendrite architecture, the lateral movement of receptor and membrane proteins of neurons, governing the availability of ion channels in the membrane, and more dynamical processes. Potential computational modes for MTs and actin filaments are only now beginning to be understood. Quantum computation in the brain would certainly be beneficial from an evolutionary perspective. It can be argued that biology has had more than 2 billion years to solve the decoherence problem by many parallel experiments. Insights into the biological and biochemical mechanisms of quantum coherent superposition and entanglement would enormously help understand consciousness’s enigmatic features. This would also undoubtedly inspire future quantum information technologies.
Finally, ultimate validation or falsification of Orch OR must be achieved by
careful experimentation. This is still very demanding since the current “gold
standard” in neuroscience is fMRI, whose spatial resolution is on the 1 mm scale
while the temporal resolution is on the 1 s scale. These parameter values are
several orders of magnitude larger than the 1 nm and 1 ns scale relevant for
tubulin’s size/time operational dimensions as studied by molecular biophysics,
let alone the quantum gravity effects hypothesized by Orch OR to be occurring on
the Planck scale of space-time geometry (10
We foresee major progress in bridging the gap between nanoscience and consciousness in nano-neuroscience areas where MT’s, actin filaments, ion channels and motor proteins connect between neurophysiology and molecular biology. Studying the nanoscale’s neural phenomena will lead to monumental breakthroughs in science and medicine and aid in consciousness studies. Further possibilities involving physically-based quantum mechanisms of consciousness should also be considered. The basic idea is to investigate if other quantum network architectures could also be operating in the brain. First of all, quantum entanglement in such a network could provide at least a partial answer to consciousness’s binding problem, allowing for a delocalized quantum state involving many neurons. This requires a thorough understanding of quantum networks. It is worth emphasizing that quantum networks may lead to quantum memories whereby entangled states store information such as visual, auditory or tactile inputs. Moreover, quantum networks could generate communication channels that would transport information and process it, performing complex operations. Recent experiments involving solid-state physics devices based on nuclear spins demonstrated that quantum information storage on the time scales of seconds and beyond is possible, as demonstrated by Tyryshkin et al. (2012) in their research on super-long quantum information storage using phosphorus ions in silicon-based materials.
However, several challenging issues still need to be elucidated. First, given the presence of thermal fluctuations, a magnetic field of sufficient strength would be needed to prepare the spin system in a sufficiently pure state. To our knowledge, there are no naturally existing large magnetic fields. Moreover, we know that strong magnetic fields, such as those produced by MRI machines, do not have a detectable effect on the state of consciousness of the person undergoing MRI scans. In terms of quantum communication channels, photon emission and absorption appear to be the best candidate mechanisms for such effects. This can be studied by researchers in the field of biophotons, which is an emerging field despite its long history of false starts and intermittent periods of dormancy. A recent review (Cifra and Pospisil, 2014) summarizes the landscape in this field, pointing to a relatively narrow range of wavelengths playing a role in biophotonics, namely between 350 and 1300 nm. The generation of photons inside living cells is mainly related to the recombination of reactive oxygen species. It is also a major puzzle to elucidate the mechanisms involved in electrical signal amplification and transmission over macroscopic distances along axons and neurons’ dendrites. The tenuous connection between quantum biology, consciousness and electromagnetic fields, if adequately supported by precise experimental investigations, could become a nexus for rigorous explorations of how our brain operates beyond the confines of conventional neuroscience.
ADP, adenosine diphosphate; ATP, adenosine triphosphate; DNA, deoxyribonucleic acid; GDP, guanosine diphosphate; GTP, guanosine triphosphate; MAP, microtubule associated protein; MHz, megahertz; MRI, magnetic resonance imaging; mRNA, messanger ribonucleic acid; MT, microtubule; Orch OR, orchestrated objective reduction.
J.A.T conceived the idea for the topic of this manuscript and wrote the paper.
This study did not require ethics approval or consent to participate.
The author thanks Prof. Roman Poznanski for valuable and insightful comments. Fruitful collaboration with Prof. Massimo Cocchi spanning the past decade is gratefully acknowledged. Numerous discussions with Dr. Lloyd Demetrius, Dr. Menas Kafatos, Sir Roger Penrose and Dr. Stuart Hameroff enabled the author to crystallize many ideas presented in this work. This study was supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada (NSERC) awarded to the author.
The author declares no conflict of interest.
Appendix associated with this article can be found, in the online version, at https://jin.imrpress.com/EN/10.31083/j.jin.2020.04.393.

