† These authors contributed equally.
The neural processing of incoming stimuli can be analysed from the electroencephalogram (EEG) through event-related potentials (ERPs). The P3 component is largely investigated as it represents an important psychophysiological marker of psychiatric disorders. This is composed by several subcomponents, such as P3a and P3b, reflecting distinct but interrelated sensory and cognitive processes of incoming stimuli. Due to the low EEG signal-to-noise-ratio, ERPs emerge only after an averaging procedure across trials and subjects. Thus, this canonical ERP analysis lacks in the ability to highlight EEG neural signatures at the level of single-subject and single-trial. In this study, a deep learning-based workflow is investigated to enhance EEG neural signatures related to P3 subcomponents already at single-subject and at single-trial level. This was based on the combination of a convolutional neural network (CNN) with an explanation technique (ET). The CNN was trained using two different strategies to produce saliency representations enhancing signatures shared across subjects or more specific for each subject and trial. Cross-subject saliency representations matched the signatures already emerging from ERPs, i.e., P3a and P3b-related activity within 350–400 ms (frontal sites) and 400–650 ms (parietal sites) post-stimulus, validating the CNN+ET respect to canonical ERP analysis. Single-subject and single-trial saliency representations enhanced P3 signatures already at the single-trial scale, while EEG-derived representations at single-subject and single-trial level provided no or only mildly evident signatures. Empowering the analysis of P3 modulations at single-subject and at single-trial level, CNN+ET could be useful to provide insights about neural processes linking sensory stimulation, cognition and behaviour.
Event-related potentials (ERPs) are small changes in the electroencephalogram
(EEG), time-locked to a stimulus or an event and reflecting the underlying neural
information processing [1]. Thanks to the high-temporal resolution of EEG
methodology, analysis of ERPs allows neural processing of an incoming stimulus to
be assessed at different stages: from earlier stages, reflected by short-latency
(
Among ERP components, P300 has gaining increasing interest in the last 50 years, since this component plays an important role as psychophysiological marker of psychiatric disorders, such as schizophrenia, bipolar disorder, autism spectrum disorder and depression [5, 6, 7, 8], and can also be used as control signal for Brain-Computer Interfaces [9]. The P300 response is an attention-dependent ERP that was first reported in EEG signals by Sutton et al. [10]. This response is characterized by a positive deflection and can be evoked in an oddball task [11], where infrequent deviant (or target) stimuli are presented to the subject immersed in a sequence of frequent background (or standard) stimuli (two-stimulus oddball task, representing the traditional oddball task). The subject attends to stimuli by responding to targets either mentally (e.g., by counting target stimuli) or physically (e.g., by pressing a button when the target stimulus occur), while ignoring other stimuli. Then, the P300 response can be analysed in the elicited ERPs and is characterized by a wave peaking within the time window between 250 and 500 ms after the stimulus onset and it is mostly distributed on the scalp around the midline EEG electrodes—Fz, Cz, Pz—increasing its magnitude from the frontal to the parietal sites [12]. The oddball P300 wave has been consistently related to attention processes, memory and contextual updating, and decision making [12, 13].
Based on results obtained while changing eliciting conditions and stimulus properties [14, 15], evidence has emerged that, rather than a single entity, the P300 could be modelled as a “late positive complex”, consisting of different positive subcomponents. In particular, at least two main subcomponents can be distinguished, in part temporally overlapped, namely P3a and P3b which have been associated to distinct, although interrelated, neural processes [12]. P3a is mostly distributed around the midline fronto-central electrodes [12] and is thought to be the marker of orientation of attention [16]. Indeed, P3a has been associated to initial reallocation of attention resulting from the detection of attribute changes in rare stimuli compared to standard ones [12, 17]. Moreover, findings suggest a relationship between stimulus deviance and P3a response, that is the greater the mismatch the larger the P3a amplitude [17, 18]. Neural sources of P3a seem to be localized in frontal structures and anterior cingulate cortex. P3b has a more posterior-parietal scalp distribution, and longer latency (by 50–100 ms) compared to P3a. It is assumed to be generated by temporal/parietal structures and to reflect the match between the stimulus and voluntarily maintained attentional trace, relevant for the task at hand, involving memory processes and context updating. According to the neuropsychological model of Polich [12], P3a and P3b reflect two cascade processes, with P3a reflecting attention engagement driven by deviant stimuli initiated in frontal structures and P3b linked to the later phase of task-related stimulus meaning evaluation and working memory comparison.
Due to the difficulty of clearly distinguishing these two components in the traditional two-stimuli oddball task, a modification of this task, resulting in a three-stimulus oddball task, is often used to elicit and investigate these two subcomponents. This paradigm is obtained by inserting a rare non-target stimulus (distractor or novel stimulus) into the sequence of rare targets and frequent standard stimuli, allowing clearly distinguishable P3a and P3b to be obtained in response to the distractor stimuli and target stimuli, respectively. In particular, being the mismatch with the target stimulus larger for the distractor than for the target, the elicited P3a is more evident in the ERPs to distractors than to targets; on the contrary, target ERPs contain a more evident P3b component than distractor ERPs, as only targets are task-relevant stimuli. Investigating both P3b and P3a components is of high interest to study cognitive functions, as they can contribute to better characterize distinct neural subprocesses and may also better discriminate between healthy and pathological conditions; for example, P3a has been shown to be more sensitive than P3b in Parkinson’s disease [19], depression [20], alcoholism [21] and psychosis [22].
EEG signals are inherently noisy; thus, ERP components emerge only after averaging across trials and subjects (grand averaging procedure), which is the canonical ERP analysis derived from EEG. Therefore, these components and their interpretation may not hold at the subject and/or trial level [23, 24]. Thus, investigating component peaks after the grand averaging procedure may hinder the ability to detect and investigate EEG features at the level of single subject or single trial, and consequently, may limit the assessment of relationships between these features and behaviour [25] and the assessment of meaningful variability across subjects and even across trials within the same subject. To overcome this limitation, EEG features can be derived without relying on canonical analysis based on ERP component peaks. To this aim, time-frequency decomposition and data-driven approaches, such as machine learning and deep learning algorithms, may represent useful processing steps to obtain reliable estimates of EEG features at the level of single-subject and single-trial, improving the capability to functionally relate EEG features to behavioural performance [25].
In particular, deep learning algorithms—representing a branch of machine learning techniques—consist of computational models designed by stacking layers of artificial neurons (deep neural networks) learning hierarchical feature representations of the input signals via multiple levels of abstraction; that is, deep neural networks learn complex non-linear functions that map inputs to feature representations. In the last decade, deep learning has gained large popularity in fields such as computer vision, speech recognition and natural language processing, to process and classify complex data such as images and time series [26]. Recently, deep neural networks have been started to be explored also with EEG, mainly for classification purposes, e.g., to discriminate among trials corresponding to different conditions during a given task [27]. The most common deep learning approach for EEG classification utilizes convolutional neural networks (CNNs) [28]. These are specialized feed-forward neural networks including convolution operators at least in one layer and are inspired by the hierarchical structure of the ventral stream of the visual system. In CNNs, neurons with specific local receptive fields are stacked on top of others; thus, receptive fields of neurons increase with the network depth and learned features increase in complexity and abstraction [29]. When CNN is trained in a supervised manner (e.g., in classification), it automatically learns classification-relevant features from the input EEG signals (i.e., class-discriminative features) based on labelled input examples (training stage), and then exploits this learning to classify previously unseen inputs (inference stage). Importantly, CNNs can be fed with raw input signals; therefore, these algorithms are capable of exploiting the entire temporal and spatial information contained in the EEG signal to extract the most class-discriminative features. This represents an important advantage compared to other more traditional machine learning techniques (mainly based on linear discriminant analysis, support vector machines, Riemannian geometry [30, 31]) that can handle only limited aspects and/or time points of the EEG data [32], thus, not accounting for the overall EEG information; hence, relevant features (and the underlying neural processes) may be ignored in these approaches. In the last years CNNs have been successfully applied to several EEG classification problems, such as the classification of motor activity both imagined and executed [33, 34, 35, 36, 37], classification of emotions [38, 39] and seizure detection [40]; furthermore, CNNs have found large application to detect the P300 event from single EEG trials [31, 33, 41, 42, 43, 44, 45], also in the perspective of use these algorithms inside Brain-Computer Interface (BCI) systems [9].
Crucially, CNNs not only represent powerful tools for EEG classification, but may also provide novel approaches to improve EEG analysis and interpretation, in particular by exploiting post-hoc (i.e., applied after the training stage) explanation techniques (ET). These are techniques aimed at explaining the features learned by the CNN and that the CNN mostly relies on to discriminate among the classes [46]. Due to the automatic feature learning provided by the CNN, the composition CNN+ET represents a useful non-linear tool to explore the neural processes involved in the classified conditions in a data-driven manner, possibly contributing to validate and also inform cognitive neuroscience knowledge. It is noteworthy that, depending on the training strategy adopted for the CNN (e.g., using signals collected across subjects or signals within single subjects), the features learned by the CNNs may evidence common neural signatures across subjects (representing general task-relevant features), or may evidence neural signatures subject-specific and variability among subjects. Among ETs, saliency maps [47] outline the features within each single input EEG trial that mostly contribute to drive the correct decision (i.e., the correct output class) in the trained CNN; hence, saliency maps represent the timepoints and channels in each EEG input trial that are more relevant for the correct classification of that input example. Since this technique outlines the relevant features in the domain of input EEG signals (which represents a directly interpretable domain), saliency maps can be easily put in relation with ERP correlates. In addition, being the classification performed at the single trial level, saliency maps outline EEG features at the time scale of single trial.
The aim of the present study is to go behind the simple application of CNNs for P3 decoding—as already amply investigated in literature [31, 33, 41, 42, 43, 44, 45]—but rather to explore the potentialities of the combination CNN+ET as a data-driven EEG analysis tool in the investigation of the electrophysiological signatures related to P3 (in particular, to its main subcomponents P3a and P3b), and to test its ability to enhance relevant signatures already at the level of single-subject and single-trial. Therefore, the novelty of this study is the formalization of a procedure CNN+ET useful for analysing meaningful features in EEG signals in response to events, and complementary to (and potentially more powerful than) the more classical ERP analysis. To this aim, we used a CNN to classify, at the level of single-trial, the EEG responses to target, distractor and standard stimuli in a 3-stimulus oddball task collected on several subjects; the CNN was realized using EEGNet, a previously validated CNN for P300 decoding [33]. Two different training strategies were adopted, training CNNs using EEG trials from all subjects and from single subjects, so that the obtained classifiers could learn common cross-subject and subject-specific class-discriminative features, respectively. Then, saliency maps were used as ET and were applied to the target and distractor classes, to highlight the spatio-temporal samples of the input that resulted more class-discriminative, potentially highlighting P3b- and P3a-related features. Three different levels of representations and analyses were possible with this approach: cross-subject, within-subject and single-trial. The contribution of this study is twofold:
(i) Test the capability of a CNN to discriminate trials in a 3-stimulus oddball tasks, automatically identifying features in the input data that correspond to relevant characteristics of the ERP response (such as different proportions of P3a and P3b manifestations), by using CNN-derived representations at the cross-subject level.
(ii) Investigate how the adopted CNN+ET combination may enhance relevant neural signatures underlying the task at hand, both at the level of single subject and of single trial, overcoming the limitation of the canonical ERP analysis derived from a grand averaging procedure over EEG trials.
In this section, first we present the three-stimulus oddball dataset. Then, we formalize the problem of decoding the EEG signals of the dataset via CNNs and how this approach, coupled with an ET, could be used as an analysis tool. Subsequently, the specific CNN architecture and training strategies adopted here are illustrated; finally, the computation of the saliency maps, used as explanation technique, is described.
In this study we adopted a public dataset [48] (available at https://openneuro.org/datasets/ds003490/versions/1.1.0) consisting of EEG signals recorded from 64 electrodes during a 3-auditory oddball task. Three stimuli were provided to 25 healthy participants for 200 ms using stereo speakers: standard stimuli (70% of trials) were 440 Hz sinusoidal tones, target stimuli (15% of trials) were 660 Hz sinusoidal tones and novel distractors (15% of trials) were sampled from a naturalistic sound dataset [49]. Participants mentally counted the number of target stimuli ignoring standard and distractor stimuli, resulting in a covert response (thus removing motor activity influences). A total number of 200 trials (140, 30 and 30 trials, respectively for standard, target and distractor conditions) were recorded for each participant. EEG was recorded at 500 Hz with reference at CPz and ground at AFz.
In order to be consistent with the reference study by Cavanagh et al. [48] where these signals were first collected and analysed, we decided to adopt here the same pre-processing pipeline as in that previous study, using the same version of the Matlab toolbox EEGlab (version 14_0_0b, Swartz Center for Computational Neuroscience, UC San Diego, CA, USA) [50]. The processing steps are described below:
(1) Removal of the very ventral electrode signals (FT9, FT10, TP9, TP10) as they tend to be unreliable.
(2) Epoching between [–2,2] s respect to stimulus onset.
(3) Re-referencing to an average reference to recover CPz activity.
(4) Identification of bad channels. To this aim, channels were separately marked for rejection computing the kurtosis of each channel finding outliers (default method used in the EEGLAB function “pop_rejchan” to perform automatic channel rejection), and applying the FASTER algorithm [51]. Channels that were automatically labelled for rejection from both previous algorithms were then rejected. Finally, bad channels were interpolated using spherical interpolation.
(5) Bad epochs were marked using the FASTER algorithm [51] and then removed. After
this step, the average number of trials per participant was reduced to 130
(6) Removal of independent components related to eye blinks.
(7) Re-referencing to an average reference.
(8) Baseline correction from –0.2 to 0 s pre-stimulus.
(9) Band-pass filtering between 0.1–20 Hz. This filtering was included in the pre-processing pipeline of [42]; furthermore, it is worth noticing that this kind of filtering was performed also in other CNN-based P3 decoding studies [31, 42, 43, 45] (however, as reported in the Discussion, we also tested the effect on CNNs performances of maintaining a large frequency content of the signals, between 0.1–40 Hz).
In addition to these steps, to reduce the size of the input in the CNN-based
decoding, we downsampled signals to 100 Hz and considered EEG in epochs between
[0,1] s post-stimulus. These steps reduced the time samples of the input to be
processed in the CNN-based decoder. Thus, after this pre-processing pipeline,
each EEG trial was a 2D matrix of shape
The EEG dataset of each subject participating in the study consisted of separated pre-processed trials (see Section 2.1) with each trial belonging to one of the conditions of interest, i.e., standard, target and distractor. Each subject-specific dataset can be denoted by:

indicating with
A CNN can be trained to realize a classifier
parametrized in the parameter array
Adopting this 2D representation, CNN inputs preserve the original EEG structure. Going further deeper in the CNN, the algorithm processes the single-trial representation exploiting hierarchically structured features finalized to discriminate among classes (e.g., standard, target or distractor conditions).
Then, the trained CNN processes test trials
where the function
 Fig. 1.
Fig. 1.Proposed data-driven EEG analysis tool: workflow and
scheme of the adopted CNN. (A) CNN+ET analysis framework. The input EEG trial
Therefore, according to this approach, each input trial
In this study we adopted EEGNet [33], a light (in terms of parameters to fit)
CNN previously validated to discriminate between target and standard stimuli in a
2-stimuli oddball paradigm. This lightweight design was chosen to reduce the risk
of overfitting, as the dataset adopted here consisted of a small number of
examples for each subject (see Section 2.1). In particular, EEGNet is the
lightest design among others proposed in the literature for P300 decoding [31];
using one of the other available CNNs (introducing
EEGNet is composed by 3 main blocks (Fig. 1B). The first one can be referred to
as a spatio-temporal block (yellow block in Fig. 1B). It first processes the
input EEG trial
The architecture comprises also layers aimed to increase the generalization of the model (i.e., regularizers), such as batch normalization and dropout layers (with a dropout probability of 0.5, see also Supplementary Section 1 and Supplementary Table 1 for further details), in addition to regularizers applied during the training phase, such as early stopping. EEGNet hyper-parameters adopted here were different compared to its original formulation [33], as we carefully chose them (see Supplementary Table 1) to keep limited the overall number of trainable parameters (consisting of only 1259 parameters) in consideration of the very small dataset handled here, in view of further reducing the risk of overfitting. CNNs were developed in PyTorch [52] and trained using a workstation equipped with an AMD Threadripper 1900X, NVIDIA TITAN V and 32 GB of RAM. Codes will be released at https://github.com/ddavidebb/CNN-based_P3_analysis.git.
The training stage of EEGNet (i.e., optimization of parameters contained in
(i) Leave-one-subject-out (LOSO) strategy. In this approach, the data of the s-th
subject were held out and used as test set (thus, the test set corresponds to the
entire dataset
(ii) Within-subject (WS) strategy. In this approach, for each s-th subject, a CNN was
trained and tested using only data for that subject, thus, realizing a
subject-specific CNN (
In both cases, a validation set composed by 20% of the training examples was extracted and used to define stop criteria (see early stopping below) for the optimization of the CNN. In WS trainings, the validation set was sampled by keeping the same class proportion as in the training set (i.e., sampling 20% of each class for each subject). In LOSO trainings the validation set was equally sampled from the 24 subjects (by sampling 20% of signals from each participant’s training set) and, in this case too, by keeping the same class proportion as in the training set.
The cross-entropy between the empirical probability distribution (defined by
training labels) and the model probability distribution (defined by CNN outputs)
was used as loss function and was minimized using the Adaptive moment estimation
(Adam) algorithm [53] with a mini-batch size of 32, learning rate of
In this study, we used the Area Under the ROC curve (AUROC) to evaluate the performance of each trained CNN in the 3-class classification task; this metrics is commonly adopted to measure performance of P3 decoding at the level of single trials [33, 42, 44], a task intrinsically characterized by class imbalance (since P3 is evoked by infrequent stimuli as opposed to frequent ones). In particular, the AUROC (evaluated on the test set for each training strategy) of each possible pairwise combination of classes (one-vs-one, OVO) was computed—i.e., standard vs. target, target vs. distractor, standard vs. distractor - and then averaged across these three combinations, obtaining a multi-class AUROC (referred as av-AUROC in this study) [54]. Furthermore, we computed also the F1 score and Area Under the Precision Recall curve (AUPR) for the classes whose neural signatures were investigated in this study (i.e., target and distractor conditions), and these further metrics are reported in the Supplementary Materials (Supplementary Table 2).
To compare the OVO AUROCs and av-AUROCs between WS and LOSO strategies, Wilcoxon
signed-rank tests were performed. To correct for multiple tests (4 in total), a
false discovery rate correction at
Once networks were trained adopting WS and LOSO strategies, a post-hoc ET was
used to derive useful representations about input spatio-temporal samples
contributing more to the discrimination of target and distractor classes to
investigate P3b- and P3a-related correlates. Here we adopted saliency maps [47]
to compute the relevance score of each sample belonging to the input layer
(overall
For each input trial

containing one saliency map paired to each input trial. Then, these 2D trial-specific saliency maps were averaged across trials belonging to target and distractor classes; in this way, a saliency map for each output class was obtained for each subject. No post-processing was applied to the so obtained maps (e.g., computing the absolute or the square value), preserving the entire information. However, as the investigated EEG correlates involve positive modulations in ERPs respect to the standard condition (i.e., P3a and P3b), in this study we focused on positive values of the saliency maps, i.e., positive (negative) perturbations of input samples that increased (decreased) the correct class score.
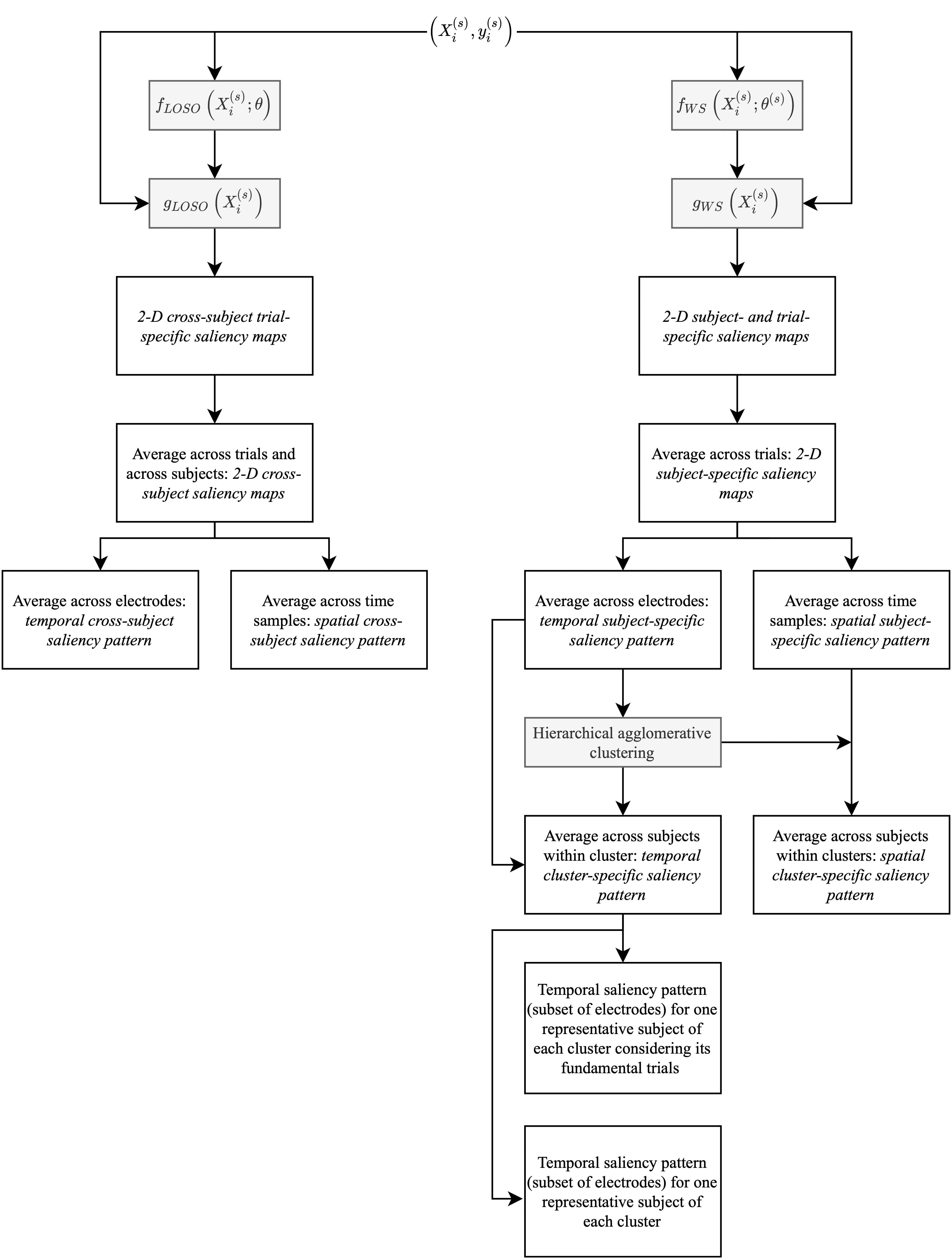 Fig. 2.
Fig. 2.Schematic diagram of the saliency map computation and
processing performed on LOSO (left branch, characterized by
The previous procedure was applied both to cross-subject CNNs obtained with the LOSO strategy and to subject-specific CNNs obtained with the WS strategy, resulting in LOSO and WS saliency maps, respectively (see the diagram in Fig. 2). In particular, for each subject two saliency maps (corresponding to target and distractor classes) were obtained both for the LOSO and WS strategies. LOSO saliency maps, being obtained from models trained on multiple subjects’ distributions, are more likely to reflect optimal class-discriminative input samples that are shared across subjects. Therefore, these representations allowed general task-related class-discriminative input samples to be inspected. Conversely, WS saliency maps—obtained from models trained on subject-specific distributions—are more likely to reflect subject-specific features. Therefore, these representations allowed the investigation of inter-subject variability of the more class-discriminative input samples.
Then, the LOSO and WS saliency maps (two maps for each subject), were subjected to different processing. In the LOSO-CNN+ET analysis pipeline, saliency maps were averaged across subjects, separately for each output class of interest, to obtain a 2D cross-subject saliency map for each output class. Then, the 2D cross-subject saliency map was also averaged across all electrodes or across all time samples, obtaining a temporal cross-subject saliency pattern and a spatial cross-subject saliency pattern, respectively. In addition, spatial cross-subject patterns were computed averaging the 2D maps only within selected time windows comprising the main peaks of the temporal cross-subject pattern. These representations allowed an analysis at the cross-subject level resulting from a grand average procedure, similarly to ERPs. Conversely, in the WS-CNN+ET analysis pipeline, saliency maps were analysed separately for each subject. For each subject, the 2D saliency map of each output class was averaged across electrodes or time samples to obtain a temporal subject-specific saliency pattern and a spatial subject-specific saliency pattern, respectively. Then, hierarchical agglomerative clustering (HAC) [56] was performed on temporal subject-specific patterns (separately for each output class of interest), to identify clusters of subjects characterized by different temporal saliency patterns. Different clusters denote different strategies adopted by the CNN in exploiting input samples to discriminate a specific class and may reflect differences across subjects in the underlying neural processes. In particular, HAC was performed using a complete linkage (i.e., farthest neighbour clustering) and adopting the correlation between observations as distance metric (see Supplementary Section 2 of Supplementary Material for a description of the adopted distance metric). Four clusters were considered and the temporal subject-specific patterns of the subjects within each cluster were averaged to obtain an average temporal saliency pattern at the level of cluster (temporal cluster-specific saliency pattern). In addition, the spatial subject-specific patterns of the subjects within each cluster (as resulted from the clustering in the temporal domain) were averaged, to obtain an average spatial saliency pattern at the level of cluster (spatial cluster-specific saliency pattern).
Finally, we performed an analysis to investigate whether the proposed CNN+ET combination could be useful to enhance correlates related to P3a and P3b at the level of single subject and single trial compared to a canonical analysis based on evoked potentials. To this aim, for each condition of interest (target and distractor), we selected a single subject belonging to each cluster, as representative of that specific cluster, and we visually evaluated to what extent the information contained in the temporal saliency pattern of that subject and condition were contained and already visible in the evoked potentials of that subject for that condition (obtained by averaging the EEG trials of that subject corresponding to that condition). To perform such comparison, for each representative subject selected, evoked potentials were averaged together within a subset of electrodes that showed more P3a and P3b components; the temporal saliency maps to be compared were obtained by averaging the 2D subject-specific saliency maps across the same subset of electrodes too (rather than across all electrodes). These subsets of electrodes were P3, P1, Pz, P2, P4, PO3, POz, PO4 (showing more P3b) for target condition and F1, Fz, F2, FC1, FCz, FC2 (showing more P3a) for distractor condition (for this choice, see ERPs in Section 3.1). In this way, the comparison was limited on a small subset of electrodes that more expressed the specific ERP component of interest. Lastly, for each of the previous temporal patterns (i.e., temporal subject-specific saliency pattern and evoked potential, each one averaged across a specific subset of electrodes) that were both obtained by averaging across trials, we considered the single constituent trials and compared the associated saliency at the level of single trial with the corresponding EEG trial, still maintaining the averaging across the specific subset of electrodes.
The grand average ERPs of the target and distractor conditions are reported in Figs. 3,4, respectively. The same representations for the standard condition are reported in Supplementary Fig. 1. These figures represent the conventional grand average across EEG trials (of the same condition) and across subjects, to obtain the evoked potentials.
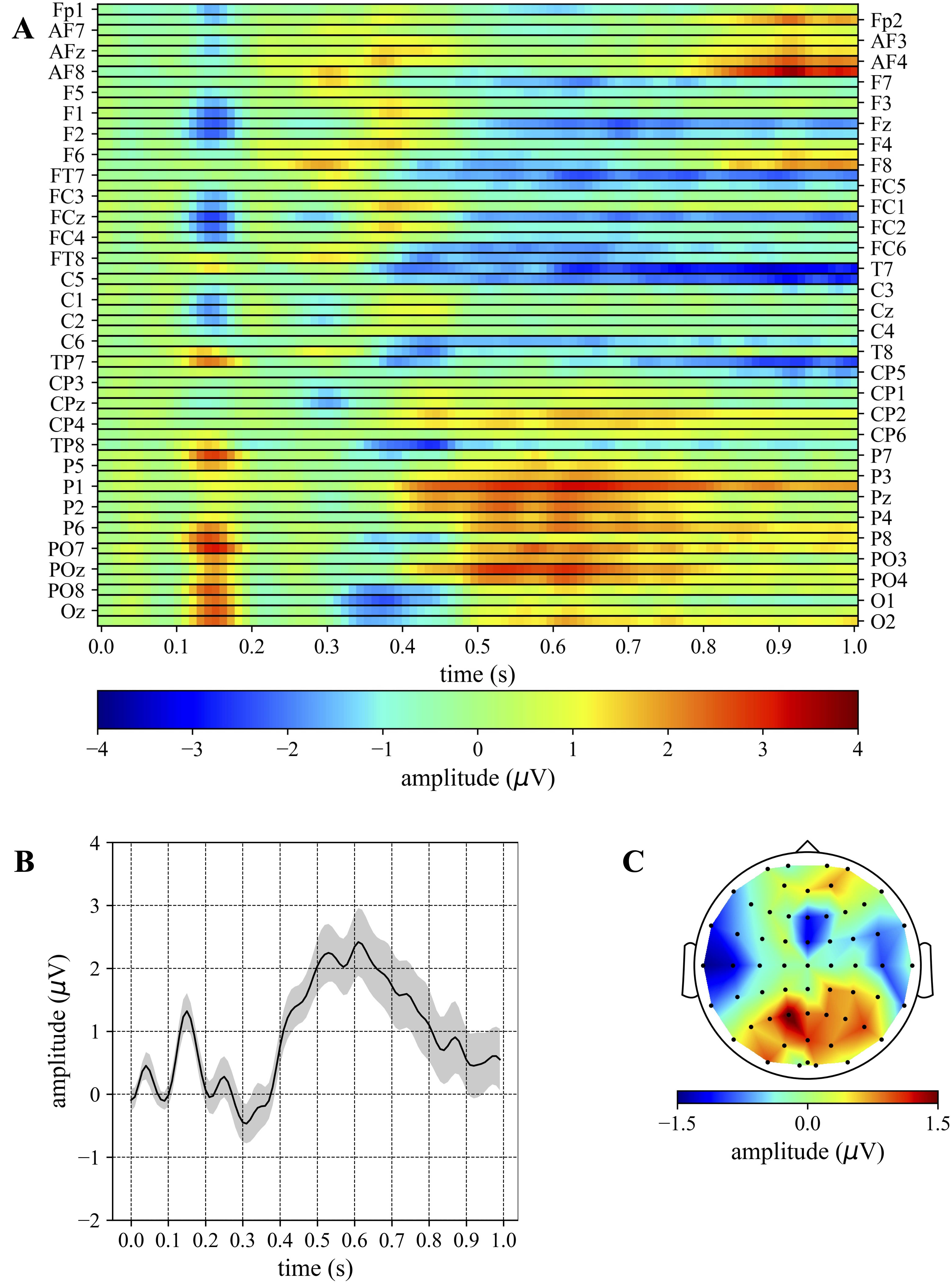 Fig. 3.
Fig. 3.Grand average ERP: target. (A) The grand average is reported as
a 2D heatmap with electrodes and time steps along rows and columns, respectively.
(B) The average temporal pattern obtained by averaging the 2D heatmap of (A)
across the subset of electrodes showing more the P3b subcomponent (P3, P1, Pz,
P2, P4, PO3, POz, PO4). The shaded area represents the mean value
 Fig. 4.
Fig. 4.Grand average ERP: distractor. (A) The grand average is
reported as a 2D heatmap with electrodes and time steps along rows and columns,
respectively. (B) The average temporal pattern obtained by averaging the 2D
heatmap of (A) across the subset of electrodes showing more the P3a subcomponent
(FC1, FC2, C1, C2, CP1, CP2). The shaded area represents the mean value
In particular, grand averages are reported for all electrodes as 2D heatmaps (Fig. 3A and Fig. 4A), showing the main P3 components, P3a and P3b, with different proportions. The P3a component can be observed especially in fronto-central/frontal regions (e.g., F1, Fz, F2, FC1, FCz, FC2, Fig. 4A) for the distractor condition while it is less evident in the same regions for the target condition (see Fig. 3A). In addition, the P3b component can be observed for the target condition in parieto-occipital/parietal regions (e.g., P3, P1, Pz, P2, P4, PO3, POz, PO4, Fig. 3A), but not for the distractor condition (Fig. 4A). Lastly, another component with a higher latency can be individuated in the distractor condition from centro-parietal to fronto-central regions (e.g., FC1, FC2, C1, C2, CP1, CP2, Fig. 4A). Averaging the activity across different subsets of electrodes showing more P3a and P3b, the timing of P3a and P3b components became clearer, i.e., averaging across P3, P1, Pz, P2, P4, PO3, POz, PO4 for the target condition (Fig. 3B) and across F1, Fz, F2, FC1, FCz, FC2 for the distractor condition (Fig. 4B) (and standard condition too, SupplementaryFig. 1B). In particular, the P3a and P3b appeared peaking within the time window 325–375 ms and 500–700 ms, respectively. Lastly, we reported also the overall spatial contribution by averaging the grand average of each electrode across all time samples (Fig. 3C and Fig. 4C), highlighting the overall topology of these components over the entire epoch (0–1000 ms).
At first, the performance of the CNN on the test set in the discrimination between the contrasted conditions needs to be analysed, to validate the CNN in the objective discrimination task and thus, evaluate whether the CNN learned useful and robust class-discriminative features. This is an important validation stage as successive steps based on the combination CNN+ET exploit features learned by this system to derive useful representations and then to analyse P3 subcomponents (see Section 2.3.5).
OVO AUROCs (mean
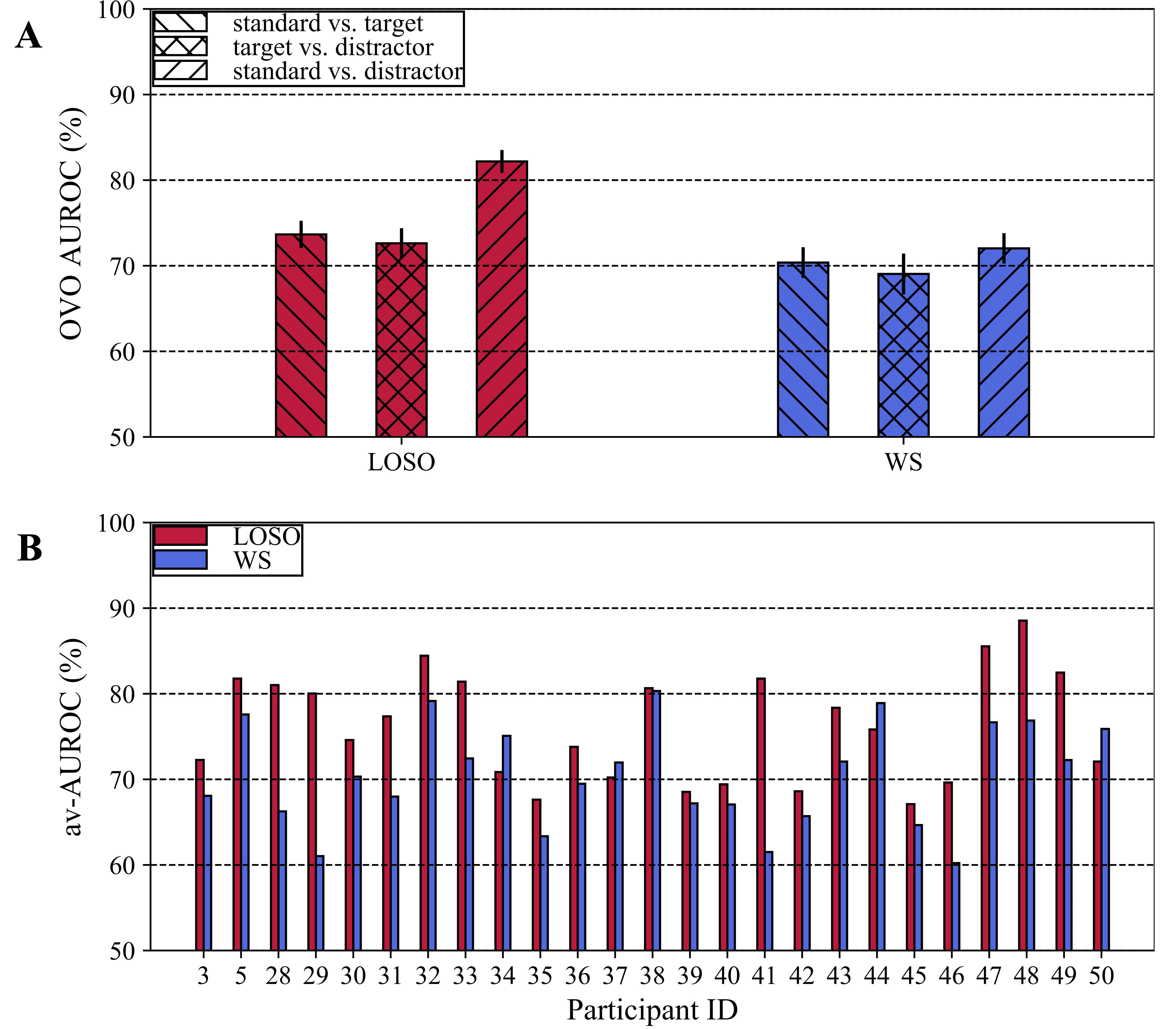 Fig. 5.
Fig. 5.CNN performance. (A) One-vs-one AUROCs using LOSO (red bars) and WS (blue bars) strategies. The height of bars denotes the mean value across subjects, while the error bar denotes the standard error of the mean. (B) Multi-class AUROCs (also referred as av-AUROCs in the manuscript) at the level of single subject obtained with the LOSO (red bars) and WS (blue bars) strategies. Note that the participant ID reported on the x-axis reflects the participant ID of the dataset.
In this section, the results obtained analysing EEG signals with the CNN+ET combination are reported. These consisted in relevance representations of the input EEG data that supported more the discrimination between the three contrasted conditions, as operated by EEGNet. In particular, the relevance is reported for target condition and distractor conditions, as the EEG response associated to these stimuli allow the analysis of P3b and P3a.
In Figs. 6,7 the 2D cross-subject saliency maps together with the derived temporal and spatial cross-subject saliency patterns are reported for target condition and distractor condition, respectively. These figures are obtained via the application of the LOSO CNN+ET procedure (see left branch in Fig. 2); therefore, they are obtained differently from Figs. 3,4 which represent the canonical grand average ERP derived directly from EEG trials.
 Fig. 6.
Fig. 6.Cross-subject saliency: target. (A) The 2D cross-subject saliency map is reported as a heatmap. (B) Temporal cross-subject saliency pattern, obtained by averaging the 2D saliency map across all electrodes. The time intervals where the saliency is higher are denoted by vertical red lines. For these specific intervals, the topological representation of the spatial cross-subject saliency pattern is also reported, obtained by averaging the saliency values of each electrode within each time interval. (C) Topological representation of the spatial cross-subject saliency map, obtained by averaging the saliency values of each electrode over the entire epoch (0–1000 ms).
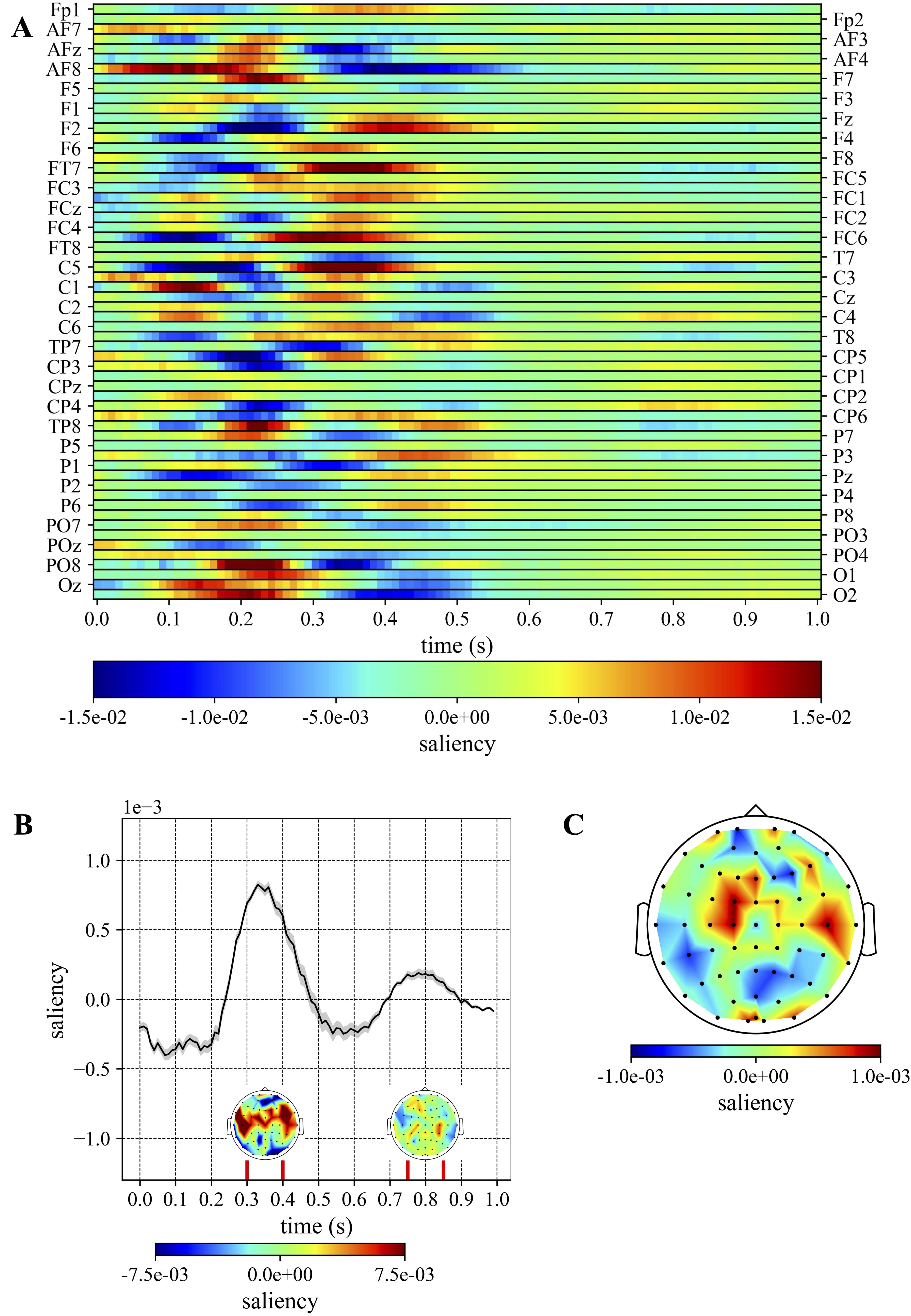 Fig. 7.
Fig. 7.Cross-subject saliency: distractor. (A) The 2D cross-subject saliency map is reported as a heatmap. (B) Temporal cross-subject saliency pattern, obtained by averaging the 2D saliency map across all electrodes. The time intervals where the saliency is higher are denoted by vertical red lines. For these specific intervals, the topological representation of the spatial cross-subject saliency pattern is also reported, obtained by averaging the saliency values of each electrode within each time interval. (C) Topological representation of the spatial cross-subject saliency map, obtained by averaging the saliency values of each electrode over the entire epoch (0–1000 ms).
Regarding the temporal cross-subject saliency patterns (Fig. 6B and Fig. 7B), the temporal windows that mostly contributed to the discrimination were different in the two conditions: they were 0–100 ms and 400–650 ms post-stimulus for the target condition (see intervals between vertical red lines in Fig. 6B), and 300–400 ms and 750–850 ms post-stimulus for the distractor condition (see intervals between vertical red lines in Fig. 7B). In addition, by visually inspecting the spatial patterns (Fig. 6C and Fig. 7C) it is evident that the electrodes more class-discriminative over the entire epoch (0–1000 ms) were parietal sites (P1, P3, P5, P7, Pz, P2, P4, P5) for the target condition and sites from central to frontal areas (C1, C6, FC1, FCz, FC2, Fz) for the distractor condition, indeed these sites are characterized by intense red colour in the map. However, distinct relevant intervals (i.e., between the vertical red lines in Fig. 6B and Fig. 7B) may be related to different electrode contributions, as reported in the spatial representations within the vertical red lines in Fig. 6B and Fig. 7B. In particular, these showed a stronger involvement of sites from parieto-occipital to centro-parietal areas within 400–650 ms than 0–100 ms post-stimulus for the target condition. In addition, for the distractor condition, the spatial distribution related to the interval 300–400 ms post-stimulus highlighted a strong involvement of sites from central to frontal areas, while within 750–850 ms post-stimulus the more contributing electrodes lied also in backward sites (e.g., centro-parietal sites).
In Figs. 8,9 the temporal (left panels, thick black lines) and spatial (right panels) cluster-specific saliency patterns for each of the 4 clusters are reported for target and distractor conditions, respectively. Left panels contain also the temporal subject-specific saliency patterns (thin black lines) belonging to each cluster.
 Fig. 8.
Fig. 8.Cluster analysis: target. For each cluster individuated by hierarchical agglomerative clustering, the left panel displays the temporal cluster-specific saliency pattern (thick line) together with the temporal subject-specific saliency patterns (thin lines) defining each cluster, while the topological map on the right displays the spatial cluster-specific saliency pattern.
 Fig. 9.
Fig. 9.Cluster analysis: distractor. For each cluster individuated by hierarchical agglomerative clustering, the left panel displays the temporal cluster-specific saliency pattern (thick line) together with the temporal subject-specific saliency patterns (thin lines) defining each cluster, while the topological map on the right displays the spatial cluster-specific saliency pattern.
For the target condition, most of the temporal subject-specific saliency
patterns turned out to be grouped into two clusters: one (cluster 4 with
Conversely, for the distractor condition, bimodal distributions appeared evident
(i.e., two main peaks can be individuated in the temporal patterns). Indeed, most
of the temporal subject-specific saliency patterns exhibited two peaks within two
temporal windows centered at around 350 ms and 750 ms (cluster 1 with
Lastly, for a single representative subject belonging to each previously computed cluster, Figs. 10,11 display the EEG evoked potentials (Fig. 10A and Fig. 11A) and the temporal saliency patterns (Fig. 10B and Fig. 11B) for the target condition and distractor condition, respectively, at the level of single subject. Specifically, Fig. 10A and Fig. 11A report the average of EEG (target or distractor) trials for the specific subject (i.e., a subject-level EEG-derived representation) while Fig. 10B and Fig. 11B report the average of the saliency associated to the same trials of the same subject (i.e., the WS CNN+ET representation). In the same figures, the corresponding patterns at the level of single trials of the same subject (Fig. 10C and Fig. 11C reporting EEG over single trials, and Fig. 10D and Fig. 11D reporting CNN-derived saliency over single trials) are shown (see Section 2.3.5 for further details about the performed processing). It is worth noticing that in this case, at variance with Figs. 8,9, the displayed quantities (both CNN-based saliency patterns and EEG patterns) refer only to a subset of electrodes (more parietal and more frontal in case of the target condition and distractor condition, respectively). It appears evident how saliency patterns (Fig. 10B,D and Fig. 11B,D) could enhance meaningful features not or only little evident in quantities directly derived from EEG, i.e., single-subject evoked potentials (Fig. 10A and Fig. 11A) and single EEG trials (Fig. 10C and Fig. 11C), see also Section 4.
 Fig. 10.
Fig. 10.Comparison between CNN-derived saliency and EEG-derived representations at single-subject and single-trial levels: target. These representations are displayed for one representative subject for each of the four clusters of Fig. 8 (each column of Fig. 10 is related to a specific cluster). (A,B) Evoked potentials directly derived from EEG trials (Fig. 10A) and temporal WS CNN-derived saliency patterns (Fig. 10B) at the level of single subject; both these representations involve averaging across trials of the same condition and across a subset of electrodes (P3, P1, Pz, P2, P4, PO3, POz, PO4). See Section 2.3.5 for details. (C,D) Single EEG trials (Fig. 10C) and WS CNN-derived saliency pattern (Fig. 10D) at the level of single trials: each row corresponds to a trial, and the representation in each row still involves averaging across the subset of electrodes. In practice, the patterns in Fig. 10A and 10B correspond to averaging, across the rows, the representations in Fig. 10C and 10D, respectively.
 Fig. 11.
Fig. 11.Comparison between CNN-derived saliency and EEG-derived representations at single-subject and single-trial levels: distractor. These representations are displayed for one representative subject for each of the four clusters of Fig. 9 (each column of Fig. 11 is related to a specific cluster). (A,B) Evoked potentials directly derived from EEG trials (Fig. 10A) and temporal WS CNN-derived saliency patterns (Fig. 10B) at the level of single subject; both these representations involve averaging across trials of the same condition and across a subset of electrodes (FC1, FC2, C1, C2, CP1, CP2). See Section 2.3.5 for details. (C,D) Single EEG trials (Fig. 10C) and WS CNN-derived saliency pattern (Fig. 10D) at the level of single trials: each row corresponds to a trial, and the representation in each row still involves averaging across the subset of electrodes. In practice, the patterns in Fig. 10A and Fig. 10B correspond to averaging, across the rows, the representations in Fig. 10C and Fig. 10D, respectively.
In this study, the combination of a CNN (here EEGNet) with an ET (here
gradient-based saliency maps) was adopted as a data-driven EEG analysis tool to
investigate the electrophysiological signatures associated to P3 subcomponents
(i.e., P3a and P3b), using EEG signals recorded during a 3-stimulus oddball
paradigm. The adopted CNN+ET, by computing input saliency representations
EEGNet scored significantly higher performance when using cross-subject distributions as input during training (LOSO) than subject-specific input distributions (WS), especially in distinguishing standards vs. distractors (see Fig. 5). This could be due to the extremely compact dataset used in this study, consisting of 188 trials on average per subject (the number of trials per subjects depended on the pre-processing procedure, see Section 2.1). Indeed, when training EEGNet with subject-specific distributions, only 170 training trials on average were used within each fold. Conversely, during LOSO trainings 24 subjects’ signals were exploited, leading to 4512 training trials on average. Therefore, despite LOSO trainings were inherently more challenging due to the subject-to-subject variability in the input distributions, EEGNet performance resulted higher than WS trainings possibly due to the availability of a larger training set. In addition, it is worth mentioning that the LOSO performance achieved by EEGNet in the addressed 3-classes decoding problem resulted similar to that obtained in more common 2-classes P300 decoding problems (i.e., target vs. standard conditions) [42], despite the increased difficulty in the classification task due to the discrimination between more than two conditions (i.e., standard vs. target vs. distractor).
Furthermore, EEGNet performance could have been affected by the specific applied
pre-processing. In this study, we kept the pre-processing pipeline unchanged
respect to the study by Cavanagh et al. [48] where the adopted dataset
was collected and presented (see Section 2.1). However, this filtering may limit
the capability of the network to autonomously identify the bands most relevant
for classification. Therefore, we tested also the CNNs performance when changing
the band-pass filtering from 0.1–20 Hz to 0.1–40 Hz in the pre-processing
pipeline; in this case the CNN could leverage additional information to solve the
decoding task or, conversely, choose to filter out unrelated information.
Providing a larger frequency content in input, a moderate but significant
improvement in CNN performance was obtained; in the LOSO strategy, av-AUROCs
improved to 77.7
When compared to ERPs (Figs. 3,4, obtained according to the canonical grand average over all EEG trials and subjects), the temporal cross-subject saliency patterns reported in Figs. 6,7 matched the P3b and P3a timings—400–650 ms and 350–400 ms post-stimulus, respectively for target stimuli and distractor stimuli (see Figs. 3B,4B,6B,7B). Similarly, the spatial cross-subject saliency patterns matched the P3b and P3a scalp distributions, both when the spatial saliency patterns were computed over all time samples (see Figs. 3C,4C,6C,7C) and within 400–650 ms and 350–400 ms post-stimulus (see Figs. 6B,7B), respectively for the target condition and distractor condition. It is worth noticing that this comparison was made possible as cross-subject saliency patterns were computed performing a grand average by construction (see Section 2.3.5), as done to obtain ERPs. From this analysis emerges the first of the main contributions of the proposed approach. Indeed, the findings suggest that the CNN, without any a priori knowledge about the neural signatures related to target and distractor stimuli, during the supervised learning was able to automatically capture meaningful class-discriminative features related to P3b and P3a. In addition, the CNN+ET combination evidenced temporal and spatial patterns that were shared across subjects (i.e., being robust across subjects), resulting from a common strategy exploited by the learning system to distinguish between the three output classes using multiple subjects’ signals (see Section 2.3.2).
Moreover, due the supervised task addressed with the CNN—i.e., discrimination from single EEG trials between standard, target and distractor stimuli—the CNN+ET was able not only to evidence correlates related to P3a and P3b, but potentially also those related to other P3 subcomponents. Indeed, other ERPs can be elicited by distractor stimuli, such as the novelty P300 (which is a third and later subcomponent after the P3b) [12, 57]; together with P3a, these components appear to be variants of the same ERP, varying on the basis of attentional and task demands. In particular, the late relevant window (750–850 ms) in the response to distractor stimuli (Fig. 7), could be related to a later component such as the novelty P300.
The cluster analysis performed on temporal subject-specific saliency patterns evidenced distinct clusters at subject-level in the temporal and spatial domains that deviated from the shared pattern across subjects discussed in the previous section (see Figs. 8,9B,C vs. Figs. 6,7B,C). Therefore, it is possible to better analyse the subject-to-subject variability, by defining clusters of subjects that responded similarly to stimuli, and differently from other subjects. In particular, temporal subject-specific saliency patterns related to target stimuli exhibited two more frequent strategies (see clusters 4, 2 in Fig. 8). These, although presenting a single positive peak and mainly involving parietal electrodes as in the corresponding general cross-subject patterns (Fig. 6B,C), revealed specific and distinguishable traits as they are centered at two slightly different time points (i.e., 500 ms and 450 ms post-stimulus) with a different dispersion across time points (i.e., cluster 2 resulted more dispersed in time) and with a different lateralization of the more contributing electrodes. When looking to patterns related to distractor stimuli in the most frequent strategy (see cluster 1 in Fig. 9, including more than half of the subjects), these patterns appeared similar to the corresponding general cross-subject patterns (in agreement with a large proportion of subjects inside the cluster), while patterns in the other clusters exhibited larger deviation from the general cross-subject patterns (e.g., see cluster 2 in Fig. 9, where temporal patterns with a single peak occurred as opposed to bimodal patterns). Finally, the cluster analysis evidenced some less reliable clusters that are less populated (e.g., cluster 1 in Fig. 8 which seems to collect exceptions rather than representing a real cluster); this may be the consequence of the small subject-specific datasets. In case of larger datasets, a larger number of trials per participant my favor the identification of meaningful features in one subject similar as in other subjects, avoiding the occurrence of cluster seemingly collecting exceptions (this may be tested in future studies on larger datasets).
Importantly, the temporal subject-specific saliency patterns (left panels in Figs. 8,9) showed relevant temporal samples potentially related to the P3b and P3a already at the level of single subject. In particular, the potential enhancement of these P3 components in saliency representations becomes clearer especially when comparing them with evoked potentials at the level of single subject. Indeed, from Figs. 10,11, temporal saliency patterns at the level of single subject enhanced the relevant processes underlying the task in all reported cases compared to the evoked potentials counterpart, where meaningful neural signatures were less clear and distinguishable (e.g., see representative patterns in Fig. 10A for clusters 1, 2 or in Fig. 11A for cluster 1). However, it is worth mentioning that in some examples the correlate was noticeable also in evoked potentials at the level of single subject (e.g., single-subject representations in Fig. 10A and Fig. 11A for cluster 4), but saliency representations resulted smoother and sharper. These considerations about saliency patterns become even more relevant at the level of single trial, where the saliency patterns seemed to preserve the well-defined temporal structure across different trials. On the contrary, single EEG trials resulted highly de-structured in time, with only few of them exhibiting P3b- and P3a-related correlates (e.g., trial 19 for the representative subject of cluster 3 of Fig. 10C, trials 19, 20 for the representative subject of cluster 1 of Fig. 11C), but without any clear coherence across recording trials, overall. From these results, the second main contribution of this study emerges, consisting in disclosing the potentialities of the CNN+ET combination to enhance the correlates related to the main P3 subcomponents (here in healthy controls) already at the single-trial level (and scaling up, at the single-subject level); the proposed method demonstrates the ability to empower the analysis of P3 modulations at the single-trial and single-subject levels, overcoming the main limitations of a canonical analysis based on evoked potentials (i.e., grand average across EEG trials and subjects). In particular, this is obtained by formalizing a processing CNN-based pipeline, that allows the analysis to be performed at multiple scales and domains (across-subjects, within-subject, within-trial, in time-space domain, or separately in the temporal and spatial domain). In prospective, the proposed data-driven analysis tool based on a CNN could be used to advance the investigation at single-subject level (e.g., to assess between-subject variability) and also at single-trial level (e.g., to assess within-subject variability by analysing differences between early vs. late recorded trials or correct/incorrect response trials), both in healthy subjects but also in patients with neurological or psychiatric disorders involving P3 alterations, e.g., Parkinson’s disease or schizophrenia. In particular, enhancing neural signatures of stimuli processing at single subject scale and at single trial scale is of great relevance to explore the functional relationships of these neural features with human performance, and to boost the comprehension of the neural processes linking sensory stimulation, cognition and behaviour.
It is worth remark that, despite deep learning-based decoders are known to require large datasets during training, the adoption of carefully designed solutions (in terms of number of parameters to fit) such as EEGNet-derived algorithms, can be used to derive useful representations in a CNN+ET framework even using small datasets, e.g., comprising less than 200 trials per subject in the addressed 3-stimulus oddball paradigm, as suggested by our results. However, the low number of trials for each subject of the adopted dataset may have affected the representations at the single-subject level, obtained with the WS strategy, and, thus, the performed analysis should be extended on larger datasets (comprising more trials per subject), to produce a more robust validation of single-subject representations.
In conclusion, we investigated the P3 in its main subcomponents with a CNN+ET workflow, analysing in a data-driven way the more important spatial and temporal samples of EEG signals in healthy controls during a 3-stimulus oddball paradigm. The composition CNN+ET, depending on the CNN training strategy (cross-subject and within-subject), was able to extract EEG neural signatures not only shared across subject (i.e., robust task-related features) as the ones obtained with a canonical ERP analysis, but also specific for each subject and for each trial, both in the temporal and spatial domains. Therefore, the CNN+ET can be seen as a transformation of EEG signals able to enhance EEG neural signatures already at the level of single trial (and scaling up at the level of single subject), providing information that could increase the understanding of the neural processes underlying the relationship between incoming sensory stimuli, cognition and behaviour.
Future developments may involve the inclusion in the workflow of elements aimed to further improve the comprehension of the learned CNN features (i.e., adoption of directly interpretable layers, not requiring post-hoc interpretation techniques) [35, 58], the adoption of larger datasets, and the application of this approach to signals recorded from patients with psychiatric disorders, for a better characterization of the neural signatures associated to these disorders and of their relationships with clinical signs, potentially contributing to characterize novel biomarkers for diagnosis and monitoring.
EEG, Electroencephalographic; ERP, Event-Related Potential; CNN, Convolutional Neural Network; BCI, Brain-Computer Interface; ET, Explanation Technique; ELU, Exponential Linear Unit; Adam, Adaptive moment estimation; WS, Within-Subject; LOSO, Leave-One-Subject-Out; ROC, Receiver Operating Characteristic; AUROC, Area Under the ROC curve; AUPR, Area Under the Precision-Recall curve; OVO, One-Vs-One; HAC, Hierarchical Agglomerative Clustering.
Conceived and designed the methodology: DB, EM. Processed data: DB. Critically analysed the data: DB, EM. Wrote the original draft: DB, EM. Reviewed and edited the manuscript: DB, EM.
In this study an open access dataset was used (https://openneuro.org/datasets/ds003490/versions/1.1.0). Refer to the study [48] for the ethics approval and consent to participation.
We gratefully acknowledge the support of NVIDIA Corporation with the donation of the TITAN V used for this research. The provider was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
This research received no external funding.
The authors declare no conflict of interest.
