The central pattern generator (CPG) is a neural circuit in the brainstem and spinal cord of vertebrates responsible for controlling the sequential activation and movement of muscles in an appropriate manner [1, 2]. While the structure of the CPG remains poorly understood, several CPG models have been developed and applied to the control of locomotion to date [3, 4, 5]. These models are generally based on neuronal models such as the Hodgkin-Huxley [6], FitzHugh-Nagumo, Morris-Lecar, and Hindmarsh-Rose models [7]. Of these, the Hindmarsh-Rose model exhibits a level of calculation simplicity that leads to its frequent application in studies exploring neural network dynamics [8, 9, 10]. Importantly, the Hindmarsh-Rose model can represent the basic properties of a CPG [10]. Accordingly, an extended Hindmarsh-Rose model [11] was herein used to simulate CPG dynamics.

Fractional calculus has been applied in many studies of neural systems, with time derivatives and fractional-order spaces allowing for the representation of differentiability, non-locality, and memory effects [12, 13]. Fractional calculus can enable the modeling of neural systems with multiple time scales, with fractional differentiation providing neurons with a fundamental computation that can contribute to information processing and stimulus anticipation [14]. There exist multiple definitions for fractional derivatives, including the Grunwald-Letnikov (GL) definition, Riemann-Liouville (RL) definition and Caputo definition. Among these definitions, the GL definition arises from the constraint of integer order difference and hold significant importance in numerical camputation [15]. Consequently, the GL definition is employed in constructing the fractional-order model in the paper. In order to consider multiple time scales, a fractional-order CPG model was established in the present study.

While there have been countless studies published to date focused on locomotion networks in mammals, the coupling relationship remains an area of active research interest [16]. Previous research efforts have addressed the association between the CPG and the motor cortex [17, 18], demonstrating that the motor cortex can control the CPG while the CPG, in turn, can regulate basic motoneuronal activation patterns and rhythms in the context of locomotion [19]. The central nervous system (CNS) includes subcritical, critical, and supercritical states [20, 21, 22], all three of which are important for the appropriate organization of complex cortical activities at different scales [23]. It is therefore important that the association between the CNS and the CPG being investigated across these three states.

Neural oscillation has been reported across a range of temporospatial scales in the CNS [24, 25], serving as an important mechanism that facilitates the communication of information within sensory neural circuits [26, 27], with the frequency of such oscillation being sensitive to external inputs. sensory neural circuits, and its frequency can be modulated by external inputs. For example, awake-behaving macaques exhibit stimulus-dependent V1 cortical gamma oscillation [28], with changes in stimulus contrast over time contributing to reliable changes in gamma frequency on a fast time scale. Accordingly, neural oscillations and network responses were both taken into consideration in the present study. When modeling neural networks, a recurrent excitation-inhibition neuronal network can capture key features including neuronal, synaptic, and network properties [21]. As such, recurrent excitation-inhibition neuronal networks have been used by researchers interested in exploring a variety of cortical activities, including irregular firing, synchronized oscillations, and neuronal avalanches [20, 21, 22, 23]. A recurrent excitation-inhibition neuronal network was thus used to simulate the CNS in this study.

In Section 2 of this article, fractional-order CPG models with time delay are studied, while coupling models with computer simulations are presented in Section 3, and Section 4 provides an overview of the key conclusions and directions for future research.

The Hindmarsh-Rose model [8, 9, 10] is represented by Eqn. 1:

(1)$$\{\begin{array}{c}\dot{x}=y-a{x}^3+b{x}^2+I-z\hfill \\ \dot{y}=c-d{x}^2-y\hfill \\ \dot{z}=r\left[S_h(x-h)-z\right]\hfill \end{array}$$

where x denotes the membrane potential in the axon of a neuron. y is the spiking variable, pertaining to the transport rate of sodium and potassium ions through fast ionic channels. z is the bursting variable, pertaining to the exchange of ions through slow ionic channels. I is an external stimulus. a, b, c, d and S${}_h$ are adjustable parameters. r is a parameter to control the current. The variable h represents the resting potential.

For this article, we consider an extended Hindmarsh-Rose model [11], as described below (Eqn. 2):

(2)$$\{\begin{array}{c}\dot{x}=y-a{x}^3+b{x}^2+I-z\hfill \\ \dot{y}=c-5x^2-y-(1/80)w\hfill \\ \dot{z}=r\left[S_h(x+1.56)-z\right]\hfill \\ \dot{w}=v[-w+e(y+0.9)]\hfill \end{array}$$

where w corresponds to the very slow exchange of calcium ions within cells between calcium stores and the cytoplasm. v and e are adjustable parameters.

Based on previous investigations [12, 13, 14, 29, 30], the neuron and the neural network have the features of fractional calculus. Inspired by these researches, the GL fractional derivative [4, 5] is introduced into the extended Hindmarsh-Rose model. And we obtain a fractional-order extended Hindmarsh-Rose model represented below (Eqn. 3):

(3)$$\{\begin{array}{c}{}^{GL}D^{\alpha }x=y-a{x}^3+b{x}^2+I-z\hfill \\ {}^{GL}D^{\alpha }y=c-5x^2-y-(1/80)w\hfill \\ {}^{GL}D^{\alpha }z=r\left[S_h(x+1.56)-z\right]\hfill \\ {}^{GL}D^{\alpha }w=v[-w+e(y+0.9)]\hfill \end{array}$$

where ${}^{GL}$D${}^{\alpha }$ denotes the GL fractional derivative operator, and $\alpha$ represents the fractional order as a non-integer number and its range located in [0, 1].

Several simulations for this proposed model were performed using an initial value of [0.1 0.1 0.1] and the following parameters: a = 1, b = 3, c = 1, v = 0.0002, r = 0.006, S${}_h$ = 4, I = 1.5, and e = 0.88. The order $\alpha$was selected within the [0.86, 0.94] range with a 0.02 step size. Fig. 1 shows the output and phase diagrams generated using this fractional-order Hindmarsh-Rose model for the different $\alpha$ values within the selected range.

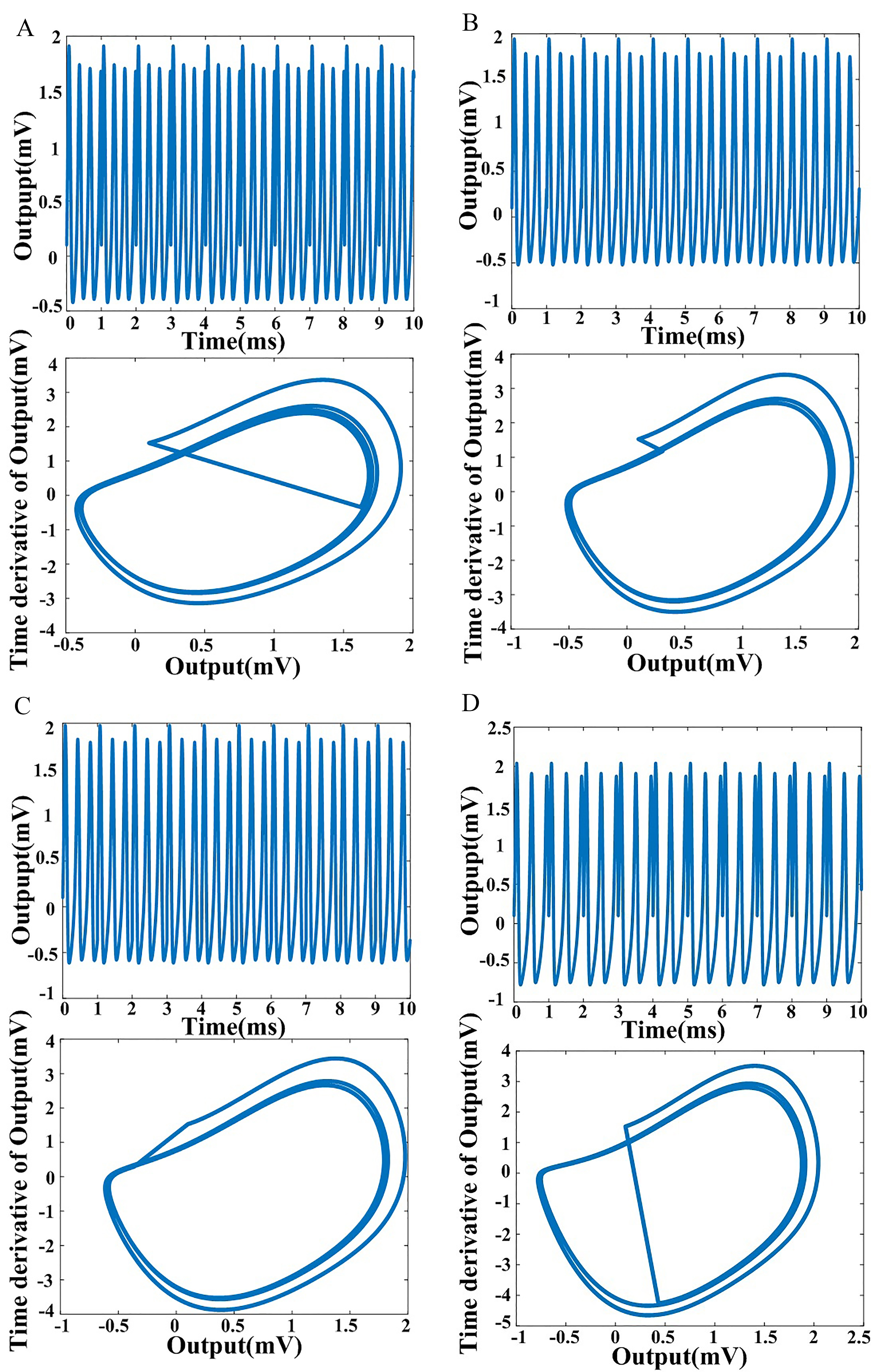Fig. 1.

Output and phase-plane diagrams for the fractional-order Hindmarsh-Rose model. (A) $\alpha$ = 0.86. (B) $\alpha$ = 0.88. (C) $\alpha$ = 0.90. (D) $\alpha$ = 0.94.

Fig. 1 shows the output and phase diagrams corresponding to fractional order values of 0.86, 0.88, 0.90, and 0.94, highlighting the fact that fractional-order systems can exhibit memory and hereditary characteristics. Prior studies have shown that neurons exhibit multiple time-scale adaptations that can be described using fractional calculus [7]. This time scale is represented by the $\alpha$ parameter, with changes in the pattern evolution of the phase diagram as $\alpha$ changes across a range of time scales.

The impulse-response function h${}_d$(t) of a time delay [8] is represented by Eqn. 4:

(4)

where A corresponds to the maximum postsynaptic potential amplitude while a${}_d$ corresponds to the sum of the characteristic delays associated with synaptic transmission. For an input m(t), the output is n(t) = h${}_d$ * m(t), where * represents the convolution operator.

A second-order ordinary differential equation can be used to mathematically represent this model (Eqn. 5):

(5)$$\ddot{n}(t)=A{a}_{d}m(t)-2a_d\dot{n}(t)-a_d^{2}n(t)$$

and this equation can be further represented as a system of two first-order differential equations,

(6)$$\{\begin{array}{c}\dot{n}(t)=p(t)\hfill \\ \dot{p}(t)=A{a}_{d}m(t)-2a_{d}p(t)-a_d{}^{2}n(t)\hfill \end{array}$$

Per Eqn. 3, x(t), y(t), z(t), w(t) are respectively replaced with m${}_i$(t)(i = 3,…,6). Per Eqn. 6, n(t) and p(t) are respectively replaced with m${}_{\mathrm{1}}$(t) and m${}_{\mathrm{2}}$(t). When the m${}_{\mathrm{3}}$(t) oscillator output served as an input for Eqn. 6, the state equations for the updated Hindmarsh-Rose model with time delay are represented below (Eqn. 7):

(7)$$\{\begin{array}{c}{}^{GL}D^{\alpha }{m}_1=m_2\hfill \\ {}^{GL}D^{\alpha }{m}_2=A{a}_d{m}_3-2a_d{m}_2-a_d{}^{2}m_1\hfill \\ {}^{GL}D^{\alpha }{m}_3=m_4-a{m}_3^3+b{m}_3^2+I-m_5\hfill \\ {}^{GL}D^{\alpha }{m}_4=c-5m_3^2-m_4-(1/80)m_6\hfill \\ {}^{GL}D^{\alpha }{m}_5=r\left[S_h\left(m_3+1.56\right)-m_5\right]\hfill \\ {}^{GL}D^{\alpha }{m}_6=v\left[-m_6+e\left(m_4+0.9\right)\right]\hfill \end{array}$$

Prior studies have employed the Hindmarsh-Rose model when simulating CPGs [19, 20]. Accordingly, the CPG was simulated with this new fractional-order extended Hindmarsh-Rose model, setting the respective A and a${}_d$ values to 3.25 and 5 in subsequent simulations.

Dynamic activity in the brain can take a range of forms including oscillatory activity, neural avalanches, and neuronal spiking. These complex multi-level variations in brain dynamics are of functional and behavioral relevance, and form the underlying basis for circuit organization. A recurrent excitation-inhibition neuronal network was thus used to explore neural circuit stimulus-response dynamics in order to better clarify the underlying neural mechanisms.

Neural processes are responsible for producing locomotor patterns, with locomotion control networks serving to regulate basic motoneuronal activation patterns and rhythms in the context of locomotion [31]. CPGs within the spinal cord are responsible for producing appropriately timed motor patterns, with each of these CPGs being subject to activation driven by locomotor command regions and to sensory feedback [32]. While there have been prior animal-based studies exploring the supraspinal control of locomotion [33], interactions between the brain and the CPG remain incompletely characterized.

3.1 Recurrent Excitation-Inhibition Neuronal Network

For neural network modeling, we adopted a biologically plausible recurrent excitation-inhibition (E-I) neural circuit model [20, 21, 22]. In this neural network, the number of excitatory neurons (NE) and the number of inhibitory neurons (NI) respectively denote the numbers of excitatory and inhibitory neurons, with a 4:1 NE to NI ratio. The default network size N for this study was 4000, with N = NE + NI. Neurons in this network were connected at random with a defined probability level of p = 0.2. The equation for the resultant neural network was as follows (Eqn. 8):

(8)$${\dot{V}}_i={\displaystyle \frac{V_{rest}^s-V_i}{{\tau }_s}}+\left(V_E^{rev}-V_i\right)\left[g_{so}E{O}_i(t)+g_{sE}E{E}_i(t)\right]+\left(V_I^{rev}-V_i\right)g_{sI}E{I}_i(t)$$

where V${}_i$ corresponds to the membrane potential of neuron i. The s parameter can be either excitatory(E) or inhibitory(I), with $V_E^{rev}$ and $V_I^{rev}$ respectively indicating the reversal potentials for excitatory and inhibitory synaptic currents (0 mV and –70 mV, respectively). EE${}_i$(t), EI${}_i$(t), and EO${}_i$(t) respectively denote input conductance from excitatory, inhibitory, and external excitatory neurons. $V_{rest}^s$ represents leaky potential and was set to –70 mV. ${\tau }_s$ is a membrane time constant, with respective ${\tau }_E$ and ${\tau }_I$ values of 20 ms and 10 ms. respectively. The synaptic strengths of conductance were set as $g_{EO}=\frac{{\widehat{g}}_{EO}}{\sqrt{N}}$, $g_{IO}=\frac{{\widehat{g}}_{IO}}{\sqrt{N}}$, $g_{EE}=\frac{{\widehat{g}}_{EE}}{\sqrt{N}}$, $g_{IE}=\frac{{\widehat{g}}_{IE}}{\sqrt{N}}$, $g_{EI}=\frac{{\widehat{g}}_{EI}}{\sqrt{N}}$, $g_{II}=\frac{{\widehat{g}}_{II}}{\sqrt{N}}$, with ${\widehat{g}}_{EO}=2.5$, ${\widehat{g}}_{IO}=4$, ${\widehat{g}}_{EE}=2$, ${\widehat{g}}_{IE}=4$, ${\widehat{g}}_{EI}=27$, ${\widehat{g}}_{II}=48$.

For the i–th neuron, the spiking train was represented by $s{p}_i(t)={\sum }_n\delta \left(t-t_i^n\right)$, with $E{E}_i(t)={\sum }_{j\in C_i^E}{F}^E*s{p}_j(t)$ and $E{I}_i(t)={\sum }_{j\in C_i^I}{F}^I*s{p}_j(t)$. The following exponential function was used to model the synaptic filter (Eqn. 9).

(9)$$F^s(t)=\frac{1}{{\tau }_d^s}\exp \left(-\frac{t}{{\tau }_d^s}\right),t\ge 0$$

For the input, EO${}_i$(t) = r${}_{i\mathit{}n}$(t) and r${}_{i\mathit{}n}$(t) = r${}_{\mathrm{0}}$ + r${}_{e\mathit{}x\mathit{}t}$(t), where r${}_{\mathrm{0}}$ and r${}_{e\mathit{}x\mathit{}t}$(t) respectively correspond to background and external inputs.

A modified second-order Runge-Kutta scheme with a 0.05 ms time step was used to simulate network dynamics [20]. A spike is emitted when the membrane potential reaches the V${}_{t\mathit{}h}$ = –50 mV threshold, after which the membrane potential is reset to V${}_{r\mathit{}e\mathit{}s\mathit{}t}$ = –60 mV. To model neuronal refractory periods, synaptic integration is then halted for 1 ms and 2 ms for inhibitory and excitatory neurons, respectively. To illustrate the network dynamics, parameters for the subcritical, critical, and supercritical states were set to r${}_{e\mathit{}x\mathit{}t}$(t) = 0, r${}_{\mathrm{0}}$ = 0.9/ms, and ${\tau }_d^E$ = 4 ms, ${\tau }_d^I$ = 4, 7, 10 ms. Simulations were run for 2000 ms with a 0.1 step size and the results were shown below.

Fig. 2 shows the raster plots and outputs for this recurrent E-I neuronal network. Fig. 2A–C correspond to subcritical, critical, and supercritical states, respectively. As shown in Fig. 2, as ${\tau }_d^I$ increases, the network state changes from subcritical to critical to supercritical. These diagrams illustrate the asynchronous state, the onset of synchrony and sparsely synchronous state. These three dynamic states have been shown to exhibit the features of E-I balance [20].

Fig. 2.

Raster plots and outputs for the established recurrent excitation-inhibition neuronal network. (A) ${\tau }_d^I$ = 4 ms. (B) ${\tau }_d^I$ = 7 ms. (C) ${\tau }_d^I$ = 10 ms.

3.2 Coupling Relationship between the Fractional-Order CPG Model and the Neural Network

Next, we established a coupling model between the fractional-order CPG model and the neural network, as shown in Fig. 3.

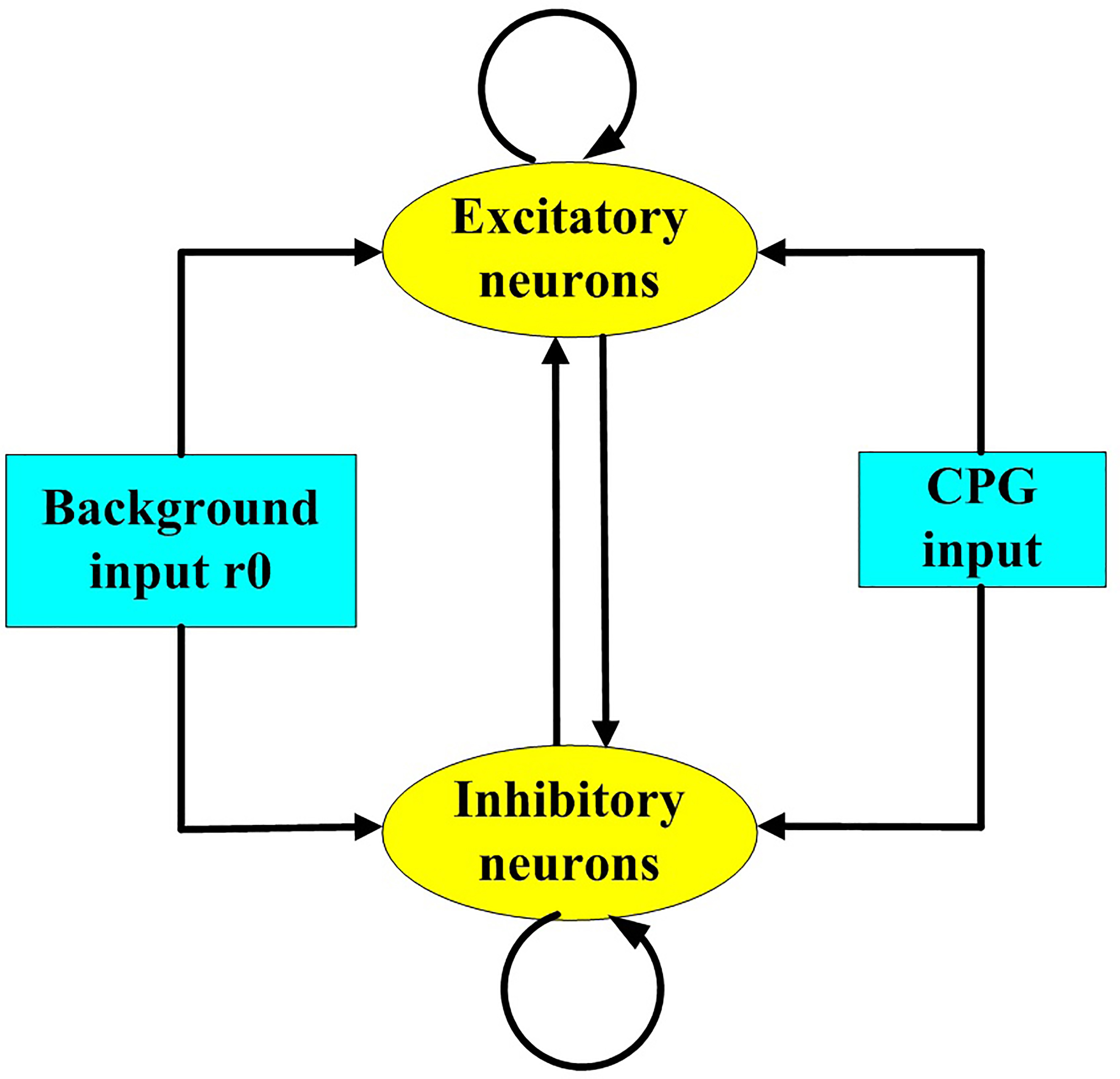Fig. 3.

Model of the coupling of the established fractional-order central pattern generators (CPG) model and the neural network.

The E-I network in Fig. 3 consists of excitatory and inhibitory neurons, each of which receives background and fractional-order CPG inputs.

A coherence index was used to estimate the synchronization of population activity [23], calculating the instantaneous population firing rate of excitatory neurons R(t) in order to establish this coherence index as follows (Eqn. 10):

(10)$$Syn=\frac{{\sigma }_R}{{\mu }_R}$$

where µ${}_R$ and ${\sigma }_R$ respectively correspond to the mean and standard deviation of R(t). Larger Syn values denote a higher degree of network synchronization.

Effects on the neural network in response to variations in CPG input values were next tested, with these inputs corresponding to 10 periods of CPG output. For these simulations, CPG effects on this neural network were explored by varying the I value in the [1, 5.5] range with a 0.5 step size and varying the fractional-order index in the [0.86, 0.94] range with a 0.02 step size.

Initially, the fractional-order index was set to 0.88, and I values were varied to obtain the power spectral density for this network in the subcritical, critical, and supercritical states (Fig. 4).

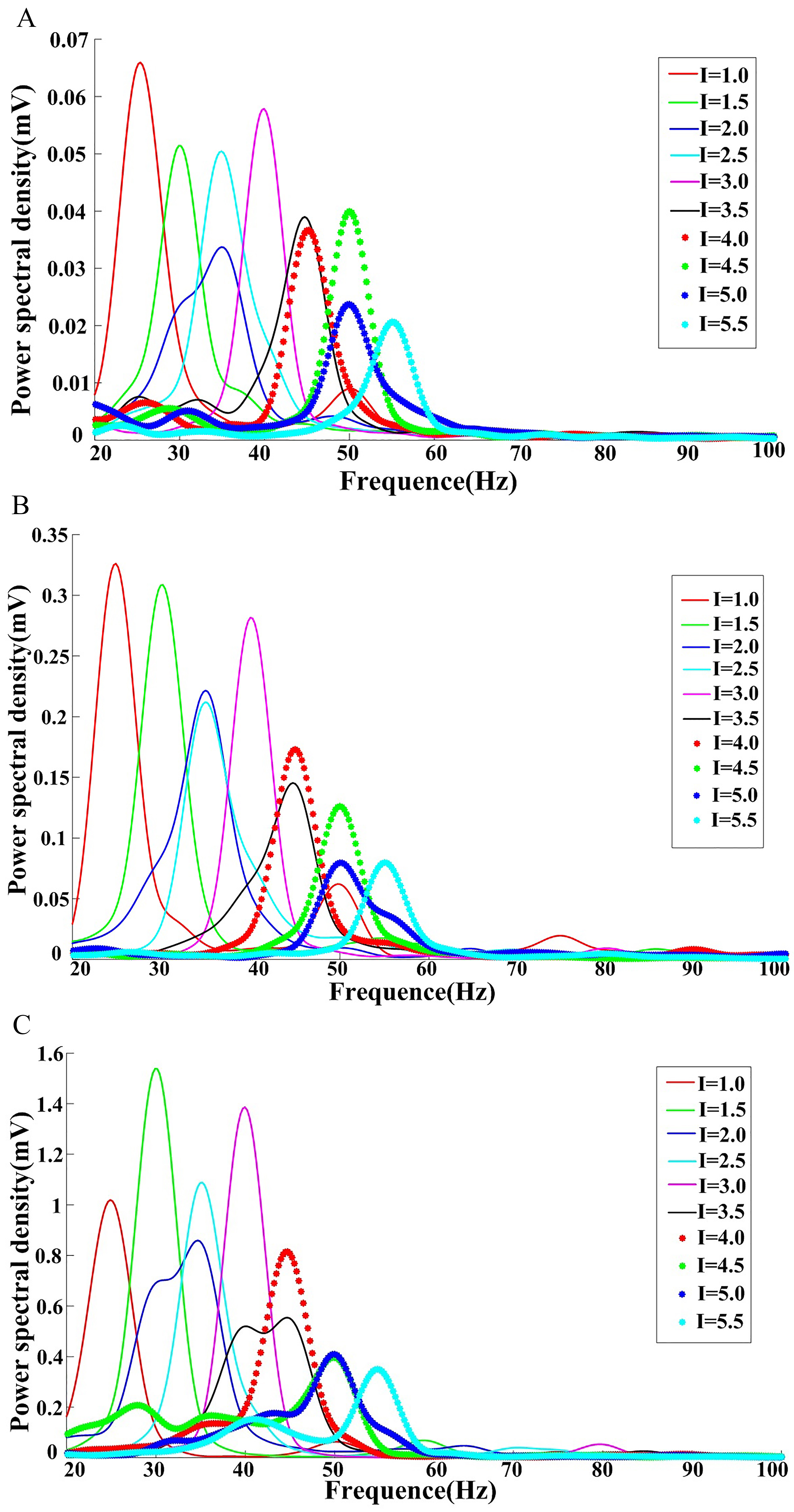Fig. 4.

Neural network power spectral density as a function of changes in the I value. Analyses were performed in the (A) subcritical, (B) critical, and (C) supercritical states.

The frequency sliding phenomenon is clear in all three states shown in Fig. 4, with peak frequency increasing as the value I rises.

The I value was then set to 3 and the fractional-order index was varied to obtain the neural network power spectral density in the subcritical, critical, and supercritical states (Fig. 5).

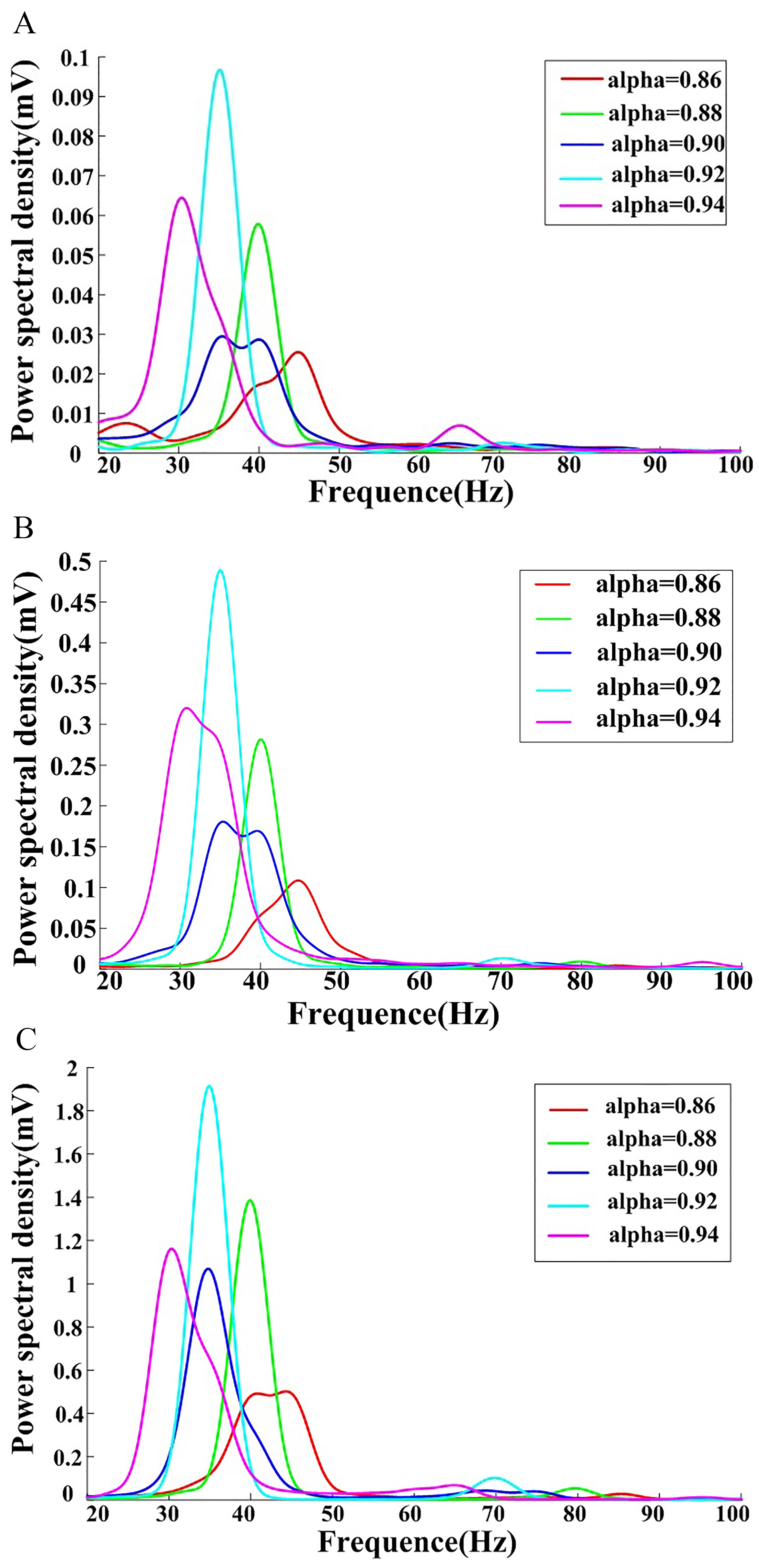Fig. 5.

Neural network power spectral density as a function of changes in the fractional-order index. Analyses were performed in the (A) subcritical, (B) critical, and (C) supercritical states.

Frequency sliding was similarly apparent in all three states shown in Fig. 5, with a decrease in peak frequency as the fractional order index increases.

Figs. 4,5 demonstrate that external stimuli and the fractional order index are responsible for the frequency sliding phenomenon, which appears to modulate brain function on multiple temporospatial scales, from the regulation of spike timing for single neurons to the coordination of large brain networks at rest and during active cognition. Frequency sliding shapes spike threshold and timing variability, and the results of the present simulations demonstrate that both external inputs and the fractional-order index can encode external sensory information and influence the spike threshold.

Next, the peak power spectral density was calculated for different external stimulus and fractional-order index values (Figs. 6,7).

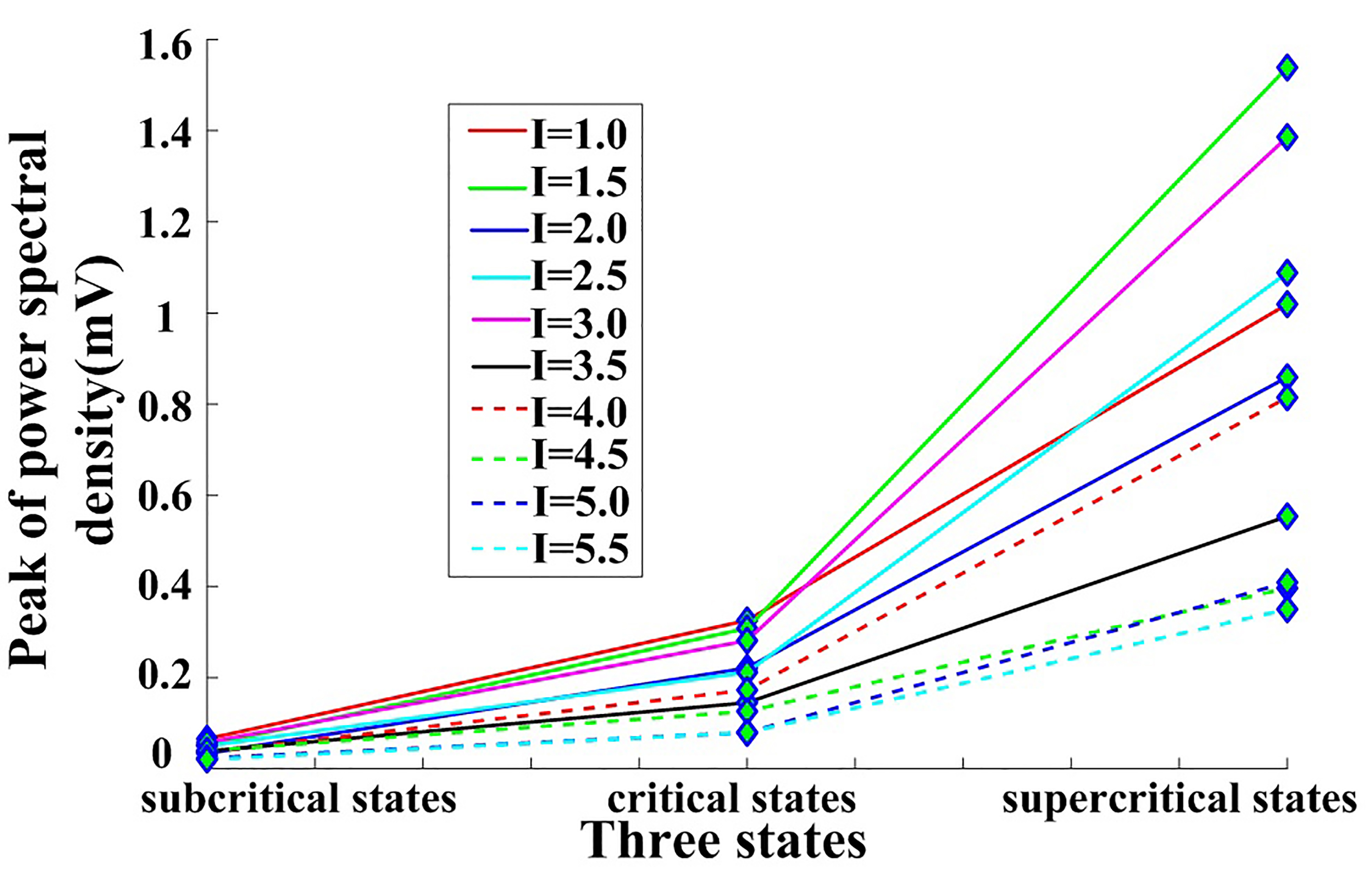Fig. 6.

Peak power spectral density for the neural network with changing I values in the subcritical, critical, and supercritical states.

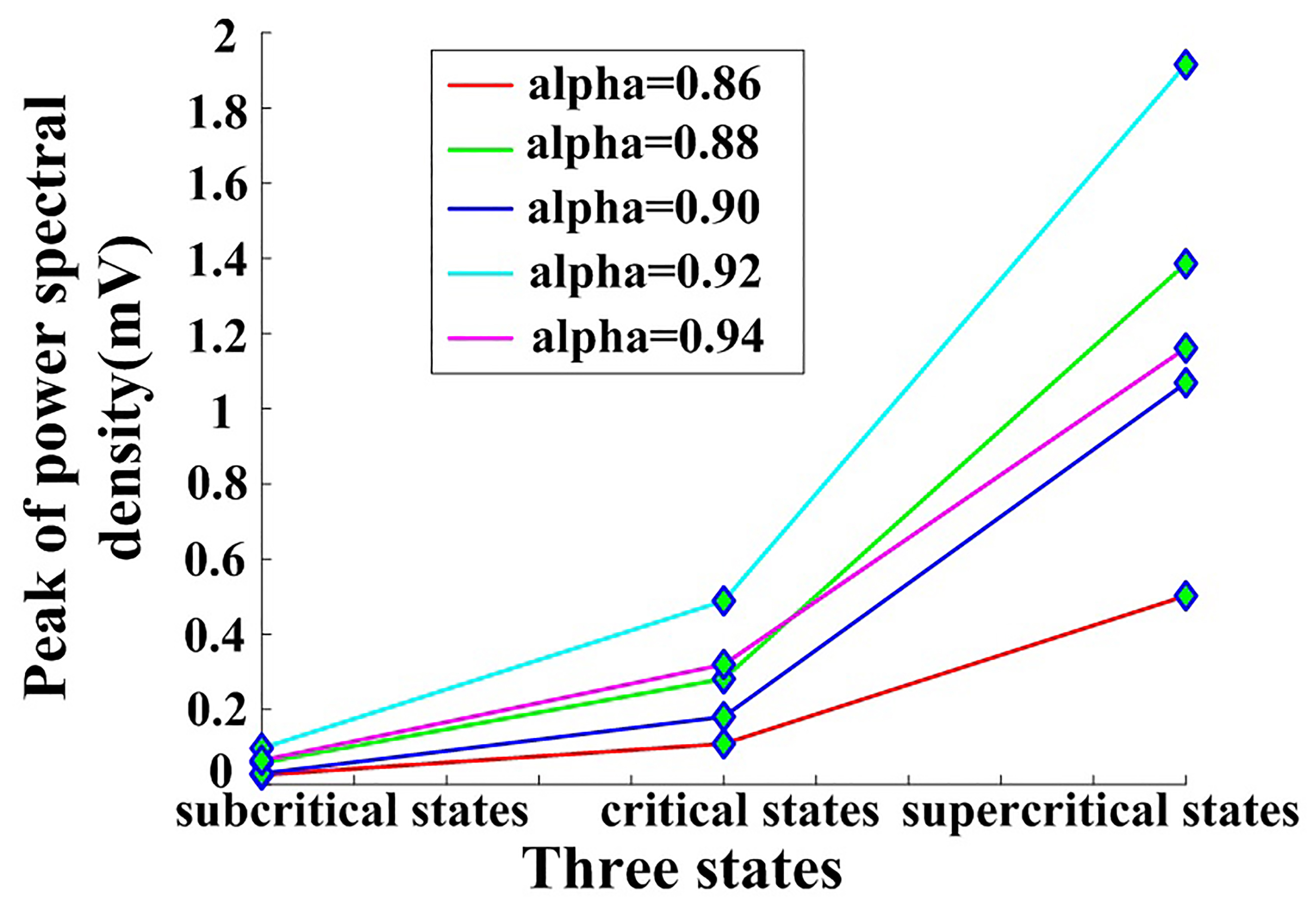Fig. 7.

Peak power spectral density for the neural network with changing fractional order index values in the subcritical, critical, and supercritical states.

The peak power spectral density shown in Fig. 6 increases with the state and changes from the subcritical to the supercritical state when fixing the external input.

As shown in Fig. 7, the peak power spectral density increases from the subcritical to the supercritical state when the fractional-order index increases. Together, Figs. 6,7 demonstrate that peak power spectral density is higher in the supercritical state relative to the subcritical or critical states owing to the higher spiking rate for the neural network in this state, in line with prior results [23].

Based on Eqn. 10, the coherence index was calculated for different external stimulus values (Fig. 8).

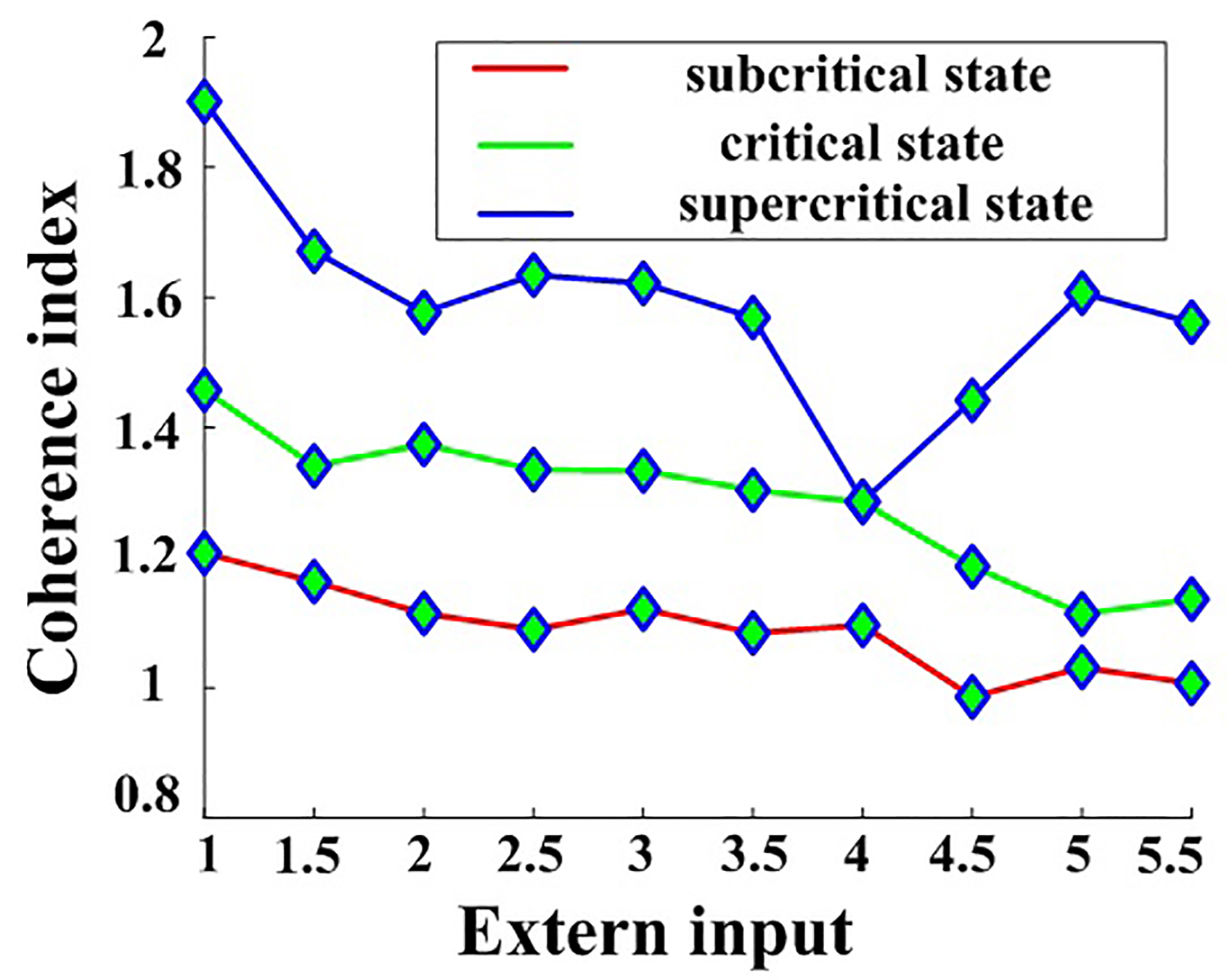Fig. 8.

Peak power spectral density for the neural network with changing I values in the subcritical, critical, and supercritical states. three states.

Although there is a minimum of coherence index in supercritical state, Fig. 8 shows a general trend that the coherence index decreases with increasing external inputs and a fixed fractional-order index of 0.88, indicating that increasing the external input will result in the desynchronization of neuronal oscillations in line with prior reports [23]. This is attributable to the greater stochasticity introduced by stronger external inputs, triggering a reduction in overall network synchronization and associated irregular neuronal firing.

The locomotion control system exhibits a high degree of biological complexity. Further studies of the coupling between the CNS and the CPG in this system will enable researchers to more fully understand the mechanisms underlying sensory information encoding and regulation.

For this study, a fractional-order CPG model based on an extended Hindmarsh-Rose model was established, while a CNS model was established using a recurrent E-I neuronal network. Models of the coupling of the CNS and the CPG were then constructed and used for digital simulations that yielded two key findings. First, these analyses demonstrated that frequency sliding is evident when the CPG is sent to the CNS in the subcritical, critical, and supercritical states with different external stimulus and fractional-order index values. Second, these findings revealed that the coherence index of the CNS declines with increasing external input values. These findings confirm that frequency sliding can regulate brain function on multiple temporospatial scales while also confirming that strong external inputs introduce neuronal stochasticity that decreases overall network synchronization.

Neurons have been shown to exhibit the ability to adapt to multiple time scales in a manner compatible with fractional calculus [14]. Fractional-order models are thus better suited than integral-order models when seeking to describe the coupling relationships within a neural system. Using these models, our study employs a novel approach to evaluating locomotion control.

Rhythmic neural network oscillations are a common phenomenon observed across many aspects of perception [34]. Different oscillatory frequencies are used by the brain for the rhythmic sampling of sensory inputs and motor activity [35]. Frequency sliding is a phenomenon that can bridge brain function across multiple temporospatial scales. While such frequency sliding is based on fundamental neuronal features, it can be applied to groups of neurons and to large-scale network connectivity [36]. Here, frequency sliding was also evident in simulations representing the coupling model between the CNS and the CPG. The primary frequency range was in the gamma band responsible for driving a range of perception-related processes [20]. This supports a model in which the locomotion system utilizes frequency sliding to sample external sensory inputs, offering insights into the underlying mechanisms that may govern locomotion.

In this paper, a fractional-order CPG model based on an extended Hindmarsh-Rose model was established. Models of the coupling of the CNS and the CPG were then constructed and used for digital simulations.These findings confirm that frequency sliding can regulate brain function on multiple temporospatial scales and the neuronal stochasticity decreases network synchronization.

The CPG is a micro neural circuits and many mathematical models are used to present the dynamics of the CPG. In these models, Rybak model [37] incorporated several neuron types into a spinal circuit network. The model provided important insights into the organization of neural circuits in the spinal cord. Then the Rybak model [37] can be used for the further CPG modelling development. Frequency mixing and cross-frequency coupling in neural systems are models that also enable the sampling of sensory information [38]. The CPG functions as a rhythmic oscillator in the spinal cord capable of modulating patterns of locomotion and exhibiting a range of frequencies. Frequency mixing and cross-frequency coupling have previously been shown to enhance locomotion control in the brain [39, 40]. Further investigations focused on such frequency mixing and the frequency coupling in the context of locomotion control are thus warranted. Njitacke et al. [41] built a electronic circuit to study the dynamics of a 2D Hindmarsh–Rose neuron. Malik et al. [42] used Field Programmable Gate Array (FPGA) to investigate the behaviors of the fractional order biological neuron. Therefore, another further research field is the circuit implementation of these models in the paper.

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

QL and XJ contributed to the conception and design of the study. QL, HW, WL, and XJ were involved in writing drafts of the manuscript and contributed to the analysis the results of the work. All authors contributed to editorial changes in the manuscript. All authors read and approved the final manuscript. All authors have participated sufficiently in the work and agreed to be accountable for all aspects of the work.

Not applicable.

Not applicable.

This research was funded by Shandong Provincial Natural Science Foundation, China, grant number ZR2022MF340.

The authors declare no conflict of interest.